|
Maximum A Posteriori
An estimation procedure that is often claimed to be part of Bayesian statistics is the maximum a posteriori (MAP) estimate of an unknown quantity, that equals the mode of the posterior density with respect to some reference measure, typically the Lebesgue measure. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. It is closely related to the method of maximum likelihood (ML) estimation, but employs an augmented optimization objective which incorporates a prior density over the quantity one wants to estimate. MAP estimation is therefore a regularization of maximum likelihood estimation, so is not a well-defined statistic of the Bayesian posterior distribution. Description Assume that we want to estimate an unobserved population parameter \theta on the basis of observations x. Let f be the sampling distribution of x, so that f(x\mid\theta) is the probability of x when the underlying population parameter is \theta. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Statistics
Bayesian statistics ( or ) is a theory in the field of statistics based on the Bayesian interpretation of probability, where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation, which views probability as the limit of the relative frequency of an event after many trials. More concretely, analysis in Bayesian methods codifies prior knowledge in the form of a prior distribution. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
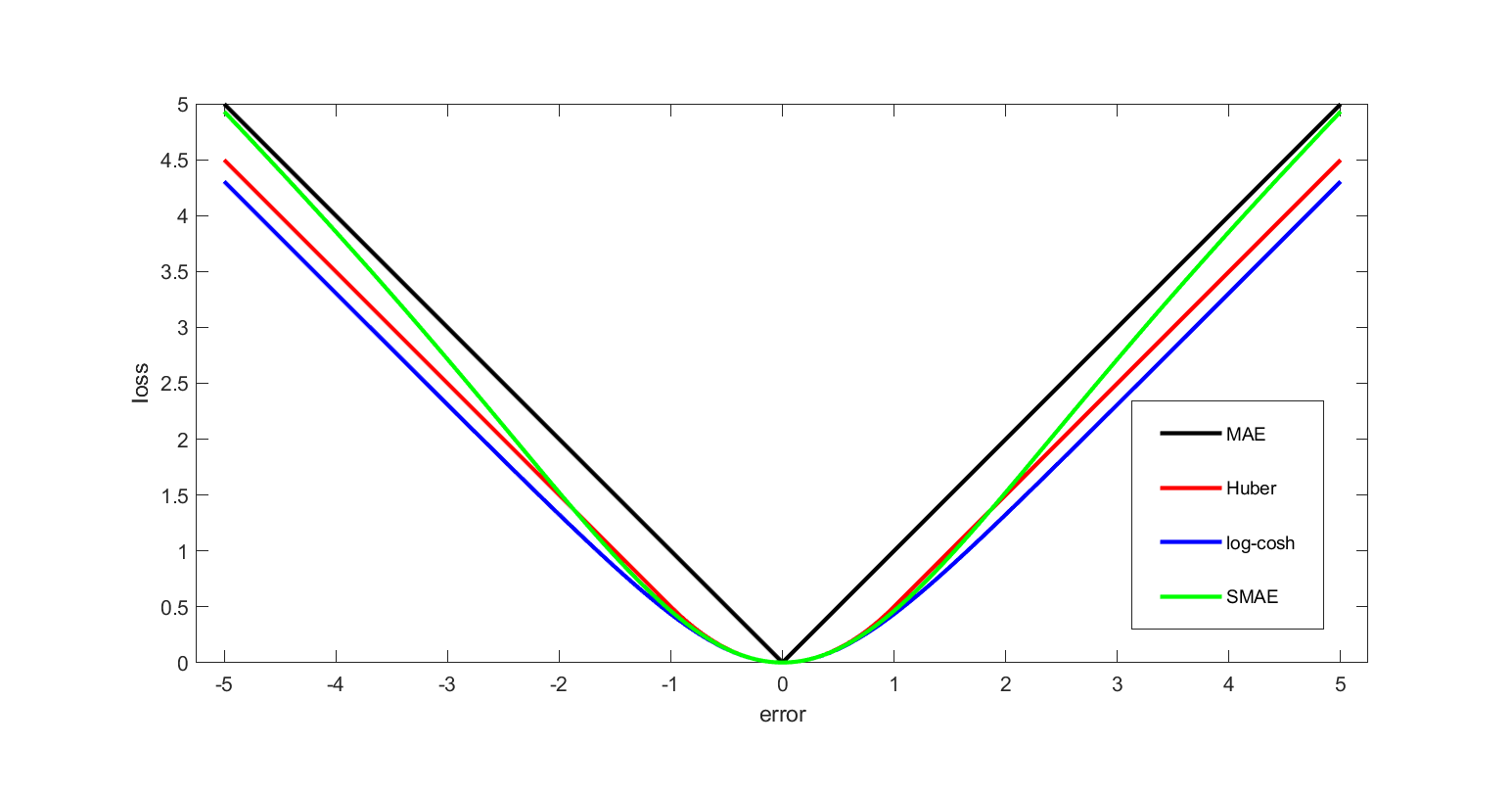
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “middle" value. The basic feature of the median in describing data compared to the Arithmetic mean, mean (often simply described as the "average") is that it is not Skewness, skewed by a small proportion of extremely large or small values, and therefore provides a better representation of the center. Median income, for example, may be a better way to describe the center of the income distribution because increases in the largest incomes alone have no effect on the median. For this reason, the median is of central importance in robust statistics. Median is a 2-quantile; it is the value that partitions a set into two equal parts. Finite set of numbers The median of a finite list of numbers is the "middle" number, when those numbers are liste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simulated Annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. For large numbers of local optima, SA can find the global optimum. It is often used when the search space is discrete (for example the traveling salesman problem, the boolean satisfiability problem, protein structure prediction, and job-shop scheduling). For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms such as gradient descent or branch and bound. The name of the algorithm comes from annealing in metallurgy, a technique involving heating and controlled cooling of a material to alter its physical properties. Both are attributes of the material that depend on their thermodynamic free energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, mathematician Stanisław Ulam, was inspired by his uncle's gambling habits. Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration, and generating draws from a probability distribution. They can also be used to model phenomena with significant uncertainty in inputs, such as calculating the risk of a nuclear power plant failure. Monte Carlo methods are often implemented using computer simulations, and they can provide approximate solutions to problems that are otherwise intractable or too complex to analyze mathematically. Monte Carlo methods are widely used in va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Method In Optimization
In calculus, Newton's method (also called Newton–Raphson) is an iterative method for finding the roots of a differentiable function f, which are solutions to the equation f(x)=0. However, to optimize a twice-differentiable f, our goal is to find the roots of f'. We can therefore use Newton's method on its derivative f' to find solutions to f'(x)=0, also known as the critical points of f. These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function f. Newton's method The central problem of optimization is minimization of functions. Let us first consider the case of univariate functions, i.e., functions of a single real variable. We will later consider the more general and more practically useful multivariate case. Given a twice differentiable function f:\mathbb\to \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Prior
In Bayesian probability theory, if, given a likelihood function p(x \mid \theta), the posterior distribution p(\theta \mid x) is in the same probability distribution family as the prior probability distribution p(\theta), the prior and posterior are then called conjugate distributions with respect to that likelihood function and the prior is called a conjugate prior for the likelihood function p(x \mid \theta). A conjugate prior is an algebraic convenience, giving a closed-form expression for the posterior; otherwise, numerical integration may be necessary. Further, conjugate priors may clarify how a likelihood function updates a prior distribution. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory.Howard Raiffa and Robert Schlaifer. ''Applied Statistical Decision Theory''. Division of Research, Graduate School of Business Administration, Harvard University, 1961. A similar c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |