|
Lattice Protein
Lattice proteins are highly simplified models of protein-like heteropolymer chains on lattice conformational space which are used to investigate protein folding. Simplification in lattice proteins is twofold: each whole residue (amino acid) is modeled as a single "bead" or "point" of a finite set of types (usually only two), and each residue is restricted to be placed on vertices of a (usually cubic) lattice. To guarantee the connectivity of the protein chain, adjacent residues on the backbone must be placed on adjacent vertices of the lattice. Steric constraints are expressed by imposing that no more than one residue can be placed on the same lattice vertex. Because proteins are such large molecules, there are severe computational limits on the simulated timescales of their behaviour when modeled in all-atom detail. The millisecond regime for all-atom simulations was not reached until 2010, and it is still not possible to fold all real proteins on a computer. Simplification signifi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Protein Folding
Protein folding is the physical process by which a protein chain is translated to its native three-dimensional structure, typically a "folded" conformation by which the protein becomes biologically functional. Via an expeditious and reproducible process, a polypeptide folds into its characteristic three-dimensional structure from a random coil. Each protein exists first as an unfolded polypeptide or random coil after being translated from a sequence of mRNA to a linear chain of amino acids. At this stage the polypeptide lacks any stable (long-lasting) three-dimensional structure (the left hand side of the first figure). As the polypeptide chain is being synthesized by a ribosome, the linear chain begins to fold into its three-dimensional structure. Folding of many proteins begins even during translation of the polypeptide chain. Amino acids interact with each other to produce a well-defined three-dimensional structure, the folded protein (the right hand side of the figure), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Diagram
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions (pressure, temperature, volume, etc.) at which thermodynamically distinct phases (such as solid, liquid or gaseous states) occur and coexist at equilibrium. Overview Common components of a phase diagram are ''lines of equilibrium'' or ''phase boundaries'', which refer to lines that mark conditions under which multiple phases can coexist at equilibrium. Phase transitions occur along lines of equilibrium. Metastable phases are not shown in phase diagrams as, despite their common occurrence, they are not equilibrium phases. Triple points are points on phase diagrams where lines of equilibrium intersect. Triple points mark conditions at which three different phases can coexist. For example, the water phase diagram has a triple point corresponding to the single temperature and pressure at which solid, liquid, and gaseous water can coexist in a stabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
X-ray Crystallography
X-ray crystallography is the experimental science determining the atomic and molecular structure of a crystal, in which the crystalline structure causes a beam of incident X-rays to diffract into many specific directions. By measuring the angles and intensities of these diffracted beams, a crystallographer can produce a three-dimensional picture of the density of electrons within the crystal. From this electron density, the mean positions of the atoms in the crystal can be determined, as well as their chemical bonds, their crystallographic disorder, and various other information. Since many materials can form crystals—such as salts, metals, minerals, semiconductors, as well as various inorganic, organic, and biological molecules—X-ray crystallography has been fundamental in the development of many scientific fields. In its first decades of use, this method determined the size of atoms, the lengths and types of chemical bonds, and the atomic-scale differences among various mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity (mathematics)
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because \begin -2 \cdot 2 &= -4 \\ 0 \cdot 2 &= 0 \\ 41 \cdot 2 &= 82 \end By contrast, −3, 5, 7, 21 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers like 1/2 or 4.201. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; otherwis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
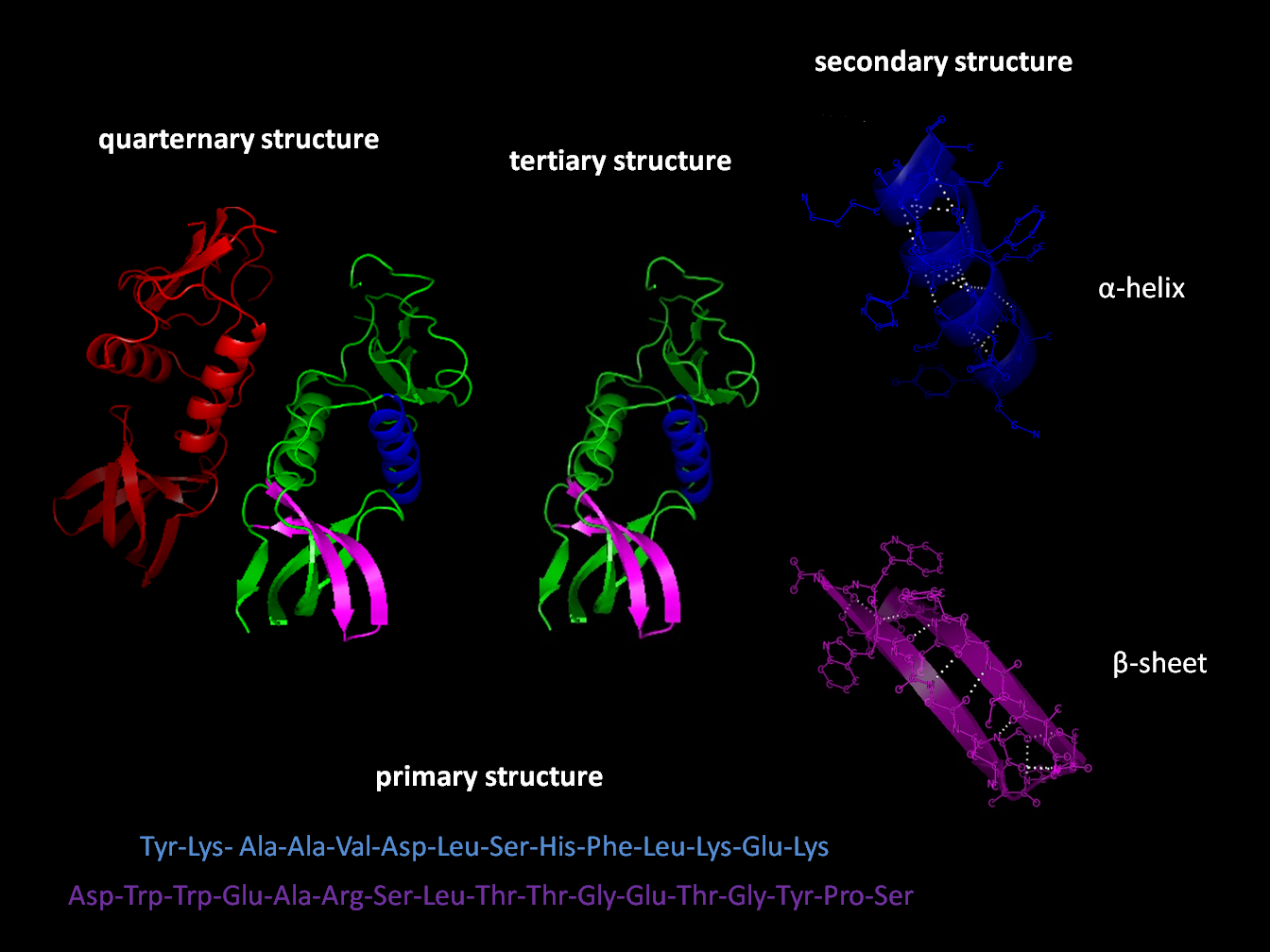
Amino Acid
Amino acids are organic compounds that contain both amino and carboxylic acid functional groups. Although hundreds of amino acids exist in nature, by far the most important are the alpha-amino acids, which comprise proteins. Only 22 alpha amino acids appear in the genetic code. Amino acids can be classified according to the locations of the core structural functional groups, as Alpha and beta carbon, alpha- , beta- , gamma- or delta- amino acids; other categories relate to Chemical polarity, polarity, ionization, and side chain group type (aliphatic, Open-chain compound, acyclic, aromatic, containing hydroxyl or sulfur, etc.). In the form of proteins, amino acid '' residues'' form the second-largest component (water being the largest) of human muscles and other tissues. Beyond their role as residues in proteins, amino acids participate in a number of processes such as neurotransmitter transport and biosynthesis. It is thought that they played a key role in enabling life ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A Surface (mathematics), surface, such as the Boundary (mathematics), boundary of a Cylinder (geometry), cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the Euclidean plane, plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Number
In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it. The ion/molecule/atom surrounding the central ion/molecule/atom is called a ligand. This number is determined somewhat differently for molecules than for crystals. For molecules and polyatomic ions the coordination number of an atom is determined by simply counting the other atoms to which it is bonded (by either single or multiple bonds). For example, r(NH3)2Cl2Br2sup>− has Cr3+ as its central cation, which has a coordination number of 6 and is described as ''hexacoordinate''. The common coordination numbers are 4, 6 and 8. Molecules, polyatomic ions and coordination complexes In chemistry, coordination number, defined originally in 1893 by Alfred Werner, is the total number of neighbors of a central atom in a molecule or ion. The concept is most commonly applied to coordin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (discrete Subgroup)
In Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has finite invariant measure. In the special case of subgroups of R''n'', this amounts to the usual geometric notion of a lattice as a periodic subset of points, and both the algebraic structure of lattices and the geometry of the space of all lattices are relatively well understood. The theory is particularly rich for lattices in semisimple Lie groups or more generally in semisimple algebraic groups over local fields. In particular there is a wealth of rigidity results in this setting, and a celebrated theorem of Grigory Margulis states that in most cases all lattices are obtained as arithmetic groups. Lattices are also well-studied in some other classes of groups, in particular groups associated to Kac–Moody algebras and automorphisms groups of regular trees (the latter are known as ''tree lattices''). Lattices are of inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Free Energy
The thermodynamic free energy is a concept useful in the thermodynamics of chemical or thermal processes in engineering and science. The change in the free energy is the maximum amount of work that a thermodynamic system can perform in a process at constant temperature, and its sign indicates whether the process is thermodynamically favorable or forbidden. Since free energy usually contains potential energy, it is not absolute but depends on the choice of a zero point. Therefore, only relative free energy values, or changes in free energy, are physically meaningful. The free energy is a thermodynamic state function, like the internal energy, enthalpy, and entropy. The free energy is the portion of any first-law energy that is available to perform thermodynamic work at constant temperature, ''i.e.'', work mediated by thermal energy. Free energy is subject to irreversible loss in the course of such work. Since first-law energy is always conserved, it is evident that free energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Landscape
An energy landscape is a mapping of possible states of a system. The concept is frequently used in physics, chemistry, and biochemistry, e.g. to describe all possible conformations of a molecular entity, or the spatial positions of interacting molecules in a system, or parameters and their corresponding energy levels, typically Gibbs free energy. Geometrically, the energy landscape is the graph of the energy function across the configuration space of the system. The term is also used more generally in geometric perspectives to mathematical optimization, when the domain of the loss function is the parameter space of some system. Applications The term is useful when examining protein folding; while a protein can theoretically exist in a nearly infinite number of conformations along its energy landscape, in reality proteins fold (or "relax") into secondary and tertiary structures that possess the lowest possible free energy. The key concept in the energy landscape approach to pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levinthal's Paradox
Levinthal's paradox is a thought experiment, also constituting a self-reference in the theory of protein folding. In 1969, Cyrus Levinthal noted that, because of the very large number of degrees of freedom in an unfolded polypeptide chain, the molecule has an astronomical number of possible conformations. An estimate of 10300 was made in one of his papers (often incorrectly cited as the 1968 paper). For example, a polypeptide of 100 residues will have 99 peptide bonds, and therefore 198 different phi and psi bond angles. If each of these bond angles can be in one of three stable conformations, the protein may misfold into a maximum of 3198 different conformations (including any possible folding redundancy). Therefore, if a protein were to attain its correctly folded configuration by sequentially sampling all the possible conformations, it would require a time longer than the age of the universe to arrive at its correct native conformation. This is true even if conformations are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |