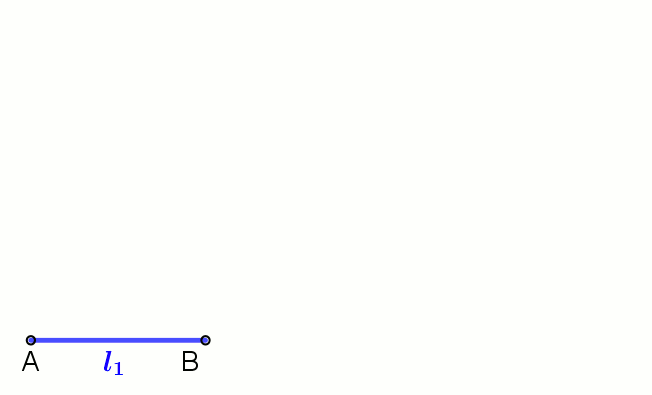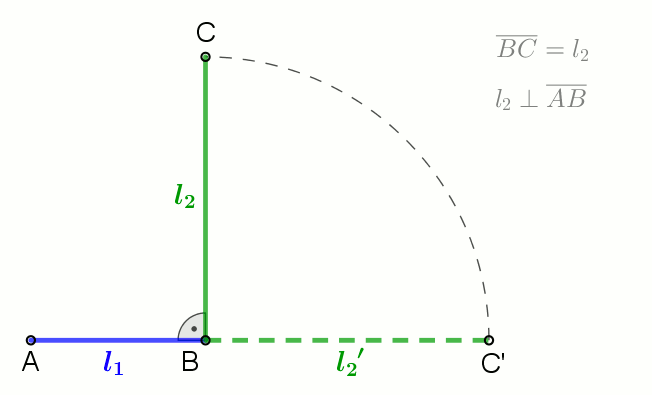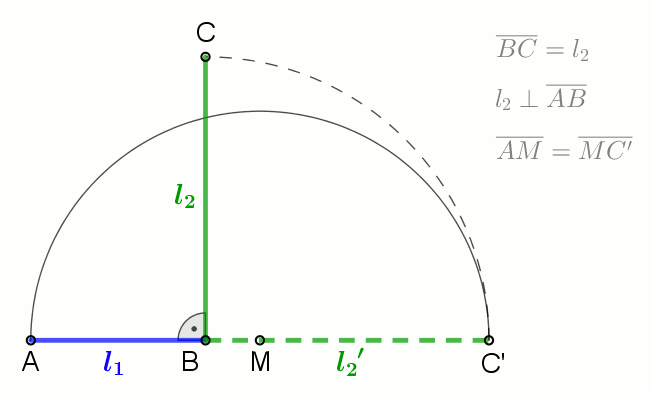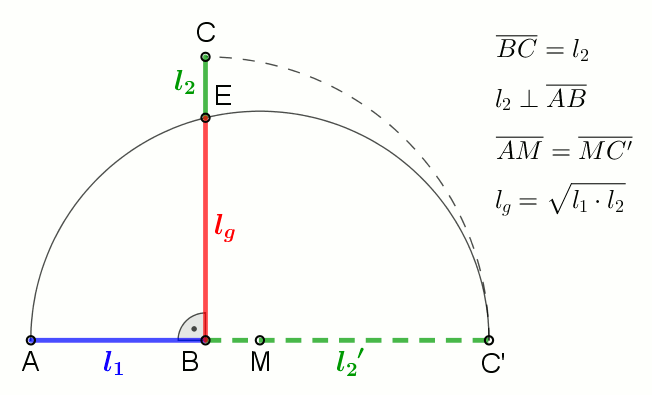|
Logarithmic Average
In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass transfer. Definition The logarithmic mean is defined as: :\begin M_\text(x, y) &= \lim_ \frac \\ pt &= \begin x & \textx = y ,\\ \frac & \text \end \end for the positive numbers x, y. Inequalities The logarithmic mean of two numbers is smaller than the arithmetic mean and the generalized mean with exponent one-third but larger than the geometric mean, unless the numbers are the same, in which case all three means are equal to the numbers. : \sqrt \leq \frac\leq \left(\frac2\right)^3 \leq \frac \qquad \text x > 0 \text y > 0. Toyesh Prakash Sharma generalizes the arithmetic logarithmic geometric mean inequality for any n belongs to the whole number as : \sqrt (\ln(\sqrt))^ (\ln(\sqrt)+n)\leq \frac\l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (mathematics)
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other examples of intervals are the set of numbers such that , the set of all real numbers \R, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton (set of one element). Real intervals play an important role in the theory of integration, because they are the simplest sets whose "length" (or "measure" or "size") is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure. Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stolarsky Mean
In mathematics, the Stolarsky mean is a generalization of the logarithmic mean. It was introduced by Kenneth B. Stolarsky in 1975. Definition For two positive real numbers ''x'', ''y'' the Stolarsky Mean is defined as: : \begin S_p(x,y) & = \lim_ \left(\right)^ \\ 0pt& = \begin x & \textx=y \\ \left(\right)^ & \text \end \end Derivation It is derived from the mean value theorem, which states that a secant line, cutting the graph of a differentiable function f at ( x, f(x) ) and ( y, f(y) ), has the same slope as a line tangent to the graph at some point \xi in the interval ,y/math>. : \exists \xi\in ,y f'(\xi) = \frac The Stolarsky mean is obtained by : \xi = f'^\left(\frac\right) when choosing f(x) = x^p. Special cases *\lim_ S_p(x,y) is the minimum. *S_(x,y) is the geometric mean. *\lim_ S_p(x,y) is the logarithmic mean. It can be obtained from the mean value theorem by choosing f(x) = \ln x. *S_(x,y) is the power mean with exponent \frac. *\lim_ S_p(x,y) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired. The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is : \left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is defined to be :H = \frac = \frac = \left(\frac\right)^. The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals. From the following formula: :H = \frac. it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs: :1/H(1/x_1 \ldots 1/x_n) = A(x_1 \ldots x_n) The harmonic mean is a Schur-conca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the '' average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, * a 0-dimensional simplex is a point, * a 1-dimensional simplex is a line segment, * a 2-dimensional simplex is a triangle, * a 3-dimensional simplex is a tetrahedron, and * a 4-dimensional simplex is a 5-cell. Specifically, a ''k''-simplex is a ''k''-dimensional polytope which is the convex hull of its ''k'' + 1 vertices. More formally, suppose the ''k'' + 1 points u_0, \dots, u_k \in \mathbb^ are affinely independent, which means u_1 - u_0,\dots, u_k-u_0 are linearly independent. Then, the simplex determined by them is the set of points : C = \left\ This representation in terms of weighted vertices is known as the barycentric coordinate system. A regular simplex is a simplex that is also a regular po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divided Difference
In mathematics, divided differences is an algorithm, historically used for computing tables of logarithms and trigonometric functions. Charles Babbage's difference engine, an early mechanical calculator, was designed to use this algorithm in its operation. Divided differences is a recursive division process. Given a sequence of data points (x_0, y_0),\ldots,(x_, y_), the method calculates the coefficients of the interpolation polynomial of these points in the Newton form. Definition Given ''n'' + 1 data points :(x_0, y_0),\ldots,(x_, y_) where the x_k are assumed to be pairwise distinct, the forward divided differences are defined as: : _k:= y_k, \qquad k \in \ : _k,\ldots,y_:= \frac, \qquad k\in\,\ j\in\. To make the recursive process of computation clearer, the divided differences can be put in tabular form, where the columns correspond to the value of ''j'' above, and each entry in the table is computed from the difference of the entries to its immediate lower le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Value Theorem (divided Differences)
In mathematical analysis, the mean value theorem for divided differences generalizes the mean value theorem to higher derivatives. Statement of the theorem For any ''n'' + 1 pairwise distinct points ''x''0, ..., ''x''''n'' in the domain of an ''n''-times differentiable function ''f'' there exists an interior point : \xi \in (\min\,\max\) \, where the ''n''th derivative of ''f'' equals ''n'' ! times the ''n''th divided difference at these points: : f _0,\dots,x_n= \frac. For ''n'' = 1, that is two function points, one obtains the simple mean value theorem. Proof Let P be the Lagrange interpolation polynomial for ''f'' at ''x''0, ..., ''x''''n''. Then it follows from the Newton form of P that the highest term of P is f _0,\dots,x_nx-x_)\dots(x-x_1)(x-x_0). Let g be the remainder of the interpolation, defined by g = f - P. Then g has n+1 zeros: ''x''0, ..., ''x''''n''. By applying Rolle's theorem first to g, then to g', a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Function
In mathematics, a homogeneous function is a function of several variables such that, if all its arguments are multiplied by a scalar, then its value is multiplied by some power of this scalar, called the degree of homogeneity, or simply the ''degree''; that is, if is an integer, a function of variables is homogeneous of degree if :f(sx_1,\ldots, sx_n)=s^k f(x_1,\ldots, x_n) for every x_1, \ldots, x_n, and s\ne 0. For example, a homogeneous polynomial of degree defines a homogeneous function of degree . The above definition extends to functions whose domain and codomain are vector spaces over a field : a function f : V \to W between two -vector spaces is ''homogeneous'' of degree k if for all nonzero s \in F and v \in V. This definition is often further generalized to functions whose domain is not , but a cone in , that is, a subset of such that \mathbf\in C implies s\mathbf\in C for every nonzero scalar . In the case of functions of several real variables and re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonic Function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if and only if it is either entirely non-increasing, or entirely non-decreasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is called ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for posi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |