|
Length Function
In the mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group. Definition A length function ''L'' : ''G'' → R+ on a group ''G'' is a function satisfying: :\beginL(e) &= 0,\\ L(g^) &= L(g)\\ L(g_1 g_2) &\leq L(g_1) + L(g_2), \quad\forall g_1, g_2 \in G. \end Compare with the axioms for a metric and a filtered algebra. Word metric An important example of a length is the word metric: given a presentation of a group by generators and relations, the length of an element is the length of the shortest word expressing it. Coxeter groups (including the symmetric group) have combinatorial important length functions, using the simple reflections as generators (thus each simple reflection has length 1). See also: length of a Weyl group element. A longest element of a Coxeter group is both important and unique up to conjugation (up to different choice of simple reflections). Prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \mathrm_n defined over a finite set of n symbols consists of the permutations that can be performed on the n symbols. Since there are n! (n factorial) such permutation operations, the order (number of elements) of the symmetric group \mathrm_n is n!. Although symmetric groups can be defined on infinite sets, this article focuses on the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the represen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring, and its basis is the set of elements of the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring. If the ring is commutative then the group ring is also referred to as a group algebra, for it is indeed an algebra over the given ring. A group algebra over a field has a further structure of a Hopf algebra; in this case, it is thus called a group Hopf algebra. The apparatus of group rings is especially useful in the theory of group representations. Definition Let ''G'' be a group, written multiplicatively, and let ''R'' be a ring. The group ring ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgroup
In group theory, a branch of mathematics, given a group ''G'' under a binary operation ∗, a subset ''H'' of ''G'' is called a subgroup of ''G'' if ''H'' also forms a group under the operation ∗. More precisely, ''H'' is a subgroup of ''G'' if the restriction of ∗ to is a group operation on ''H''. This is often denoted , read as "''H'' is a subgroup of ''G''". The trivial subgroup of any group is the subgroup consisting of just the identity element. A proper subgroup of a group ''G'' is a subgroup ''H'' which is a proper subset of ''G'' (that is, ). This is often represented notationally by , read as "''H'' is a proper subgroup of ''G''". Some authors also exclude the trivial group from being proper (that is, ). If ''H'' is a subgroup of ''G'', then ''G'' is sometimes called an overgroup of ''H''. The same definitions apply more generally when ''G'' is an arbitrary semigroup, but this article will only deal with subgroups of groups. Subgroup tests Suppose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sublevel Set
In mathematics, a level set of a real-valued function of real variables is a set where the function takes on a given constant value , that is: : L_c(f) = \left\~, When the number of independent variables is two, a level set is called a level curve, also known as ''contour line'' or ''isoline''; so a level curve is the set of all real-valued solutions of an equation in two variables and . When , a level set is called a level surface (or ''isosurface''); so a level surface is the set of all real-valued roots of an equation in three variables , and . For higher values of , the level set is a level hypersurface, the set of all real-valued roots of an equation in variables. A level set is a special case of a fiber. Alternative names Level sets show up in many applications, often under different names. For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filtered Group
In mathematics, a filtration \mathcal is an indexed family (S_i)_ of subobjects of a given algebraic structure S, with the index i running over some totally ordered index set I, subject to the condition that ::if i\leq j in I, then S_i\subseteq S_j. If the index i is the time parameter of some stochastic process, then the filtration can be interpreted as representing all historical but not future information available about the stochastic process, with the algebraic structure S_i gaining in complexity with time. Hence, a process that is adapted to a filtration \mathcal is also called non-anticipating, because it cannot "see into the future". Sometimes, as in a filtered algebra, there is instead the requirement that the S_i be subalgebras with respect to some operations (say, vector addition), but not with respect to other operations (say, multiplication) that satisfy only S_i \cdot S_j \subseteq S_, where the index set is the natural numbers; this is by analogy with a graded ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longest Element Of A Coxeter Group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by ''w''0. See and . Properties * A Coxeter group has a longest element if and only if it is finite; "only if" is because the size of the group is bounded by the number of words of length less than or equal to the maximum. * The longest element of a Coxeter group is the unique maximal element with respect to the Bruhat order. * The longest element is an involution (has order 2: w_0^ = w_0), by uniqueness of maximal length (the inverse of an element has the same length as the element). * For any w \in W, the length satisfies \ell(w_0w) = \ell(w_0) - \ell(w). * A reduced expression for the longest element is not in general unique. * In a reduced expression for the longest element, every simple reflection must occur at least once. * If the Coxeter group is finite t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length Of A Weyl Group Element
In mathematics, the length of an element ''w'' in a Weyl group ''W'', denoted by ''l''(''w''), is the smallest number ''k'' so that ''w'' is a product of ''k'' reflections by simple roots. (So, the notion depends on the choice of a positive Weyl chamber.) In particular, a simple reflection has length one. The function ''l'' is then an integer-valued function of ''W''; it is a length function In the mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group. Definition A length function ''L'' : ''G'' → R+ on a group ''G'' is a function sati ... of ''W''. It follows immediately from the definition that ''l''(''w''−1) = ''l''(''w'') and that ''l''(''ww'''−1) ≤ ''l''(''w'') + ''l''(''w' ''). References * {{cite book, last1=Kac, first1=Victor G., title=Infinite dimensional Lie algebras, date=1994, publisher=Cambridge University Press, location=Cambridge, isbn=9780521466936, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups , and finite Coxeter groups were classified in 1935 . Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
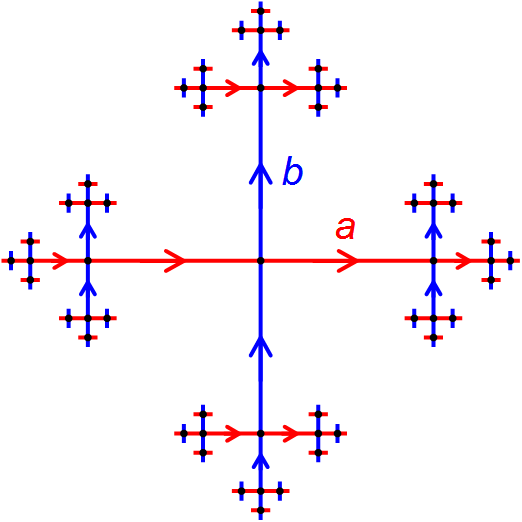
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology, hyperbolic geometry, algebraic topology, computational group theory and dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Presentation Of A Group
In mathematics, a presentation is one method of specifying a group. A presentation of a group ''G'' comprises a set ''S'' of generators—so that every element of the group can be written as a product of powers of some of these generators—and a set ''R'' of relations among those generators. We then say ''G'' has presentation :\langle S \mid R\rangle. Informally, ''G'' has the above presentation if it is the "freest group" generated by ''S'' subject only to the relations ''R''. Formally, the group ''G'' is said to have the above presentation if it is isomorphic to the quotient of a free group on ''S'' by the normal subgroup generated by the relations ''R''. As a simple example, the cyclic group of order ''n'' has the presentation :\langle a \mid a^n = 1\rangle, where 1 is the group identity. This may be written equivalently as :\langle a \mid a^n\rangle, thanks to the convention that terms that do not include an equals sign are taken to be equal to the group identit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Metric
In group theory, a word metric on a discrete group G is a way to measure distance between any two elements of G . As the name suggests, the word metric is a metric on G , assigning to any two elements g , h of G a distance d(g,h) that measures how efficiently their difference g^ h can be expressed as a word whose letters come from a generating set for the group. The word metric on ''G'' is very closely related to the Cayley graph of ''G'': the word metric measures the length of the shortest path in the Cayley graph between two elements of ''G''. A generating set for G must first be chosen before a word metric on G is specified. Different choices of a generating set will typically yield different word metrics. While this seems at first to be a weakness in the concept of the word metric, it can be exploited to prove theorems about geometric properties of groups, as is done in geometric group theory. Examples The group of integers Z The group of integers Z is generat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |