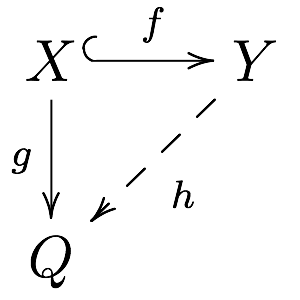|
Injective Envelope
In mathematics, particularly in algebra, the injective hull (or injective envelope) of a module is both the smallest injective module containing it and the largest essential extension of it. Injective hulls were first described in . Definition A module ''E'' is called the injective hull of a module ''M'', if ''E'' is an essential extension of ''M'', and ''E'' is injective. Here, the base ring is a ring with unity, though possibly non-commutative. Examples * An injective module is its own injective hull. * The injective hull of an integral domain is its field of fractions . * The injective hull of a cyclic ''p''-group (as Z-module) is a Prüfer group . * The injective hull of ''R''/rad(''R'') is Hom''k''(''R'',''k''), where ''R'' is a finite-dimensional ''k''-algebra with Jacobson radical rad(''R'') . * A simple module is necessarily the socle of its injective hull. * The injective hull of the residue field of a discrete valuation ring (R,\mathfrak,k) where \mathfrak = x\c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonsingular Ring
In the branches of abstract algebra known as ring theory and module theory, each right (resp. left) ''R''-module ''M'' has a singular submodule consisting of elements whose annihilators are essential right (resp. left) ideals in ''R''. In set notation it is usually denoted as \mathcal(M)=\\,. For general rings, \mathcal(M) is a good generalization of the torsion submodule tors(''M'') which is most often defined for domains. In the case that ''R'' is a commutative domain, \operatorname(M) = \mathcal(M). If ''R'' is any ring, \mathcal(R_R) is defined considering ''R'' as a right module, and in this case \mathcal(R_R) is a two-sided ideal of ''R'' called the right singular ideal of ''R''. The left handed analogue \mathcal(_R R) is defined similarly. It is possible for \mathcal(R_R) \neq \mathcal(_R R). Definitions Here are several definitions used when studying singular submodules and singular ideals. In the following, ''M'' is an ''R''-module: *''M'' is called a singular modu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Hull
In abstract algebra, specifically in module theory, a dense submodule of a module is a refinement of the notion of an essential submodule. If ''N'' is a dense submodule of ''M'', it may alternatively be said that "''N'' ⊆ ''M'' is a rational extension". Dense submodules are connected with rings of quotients in noncommutative ring theory. Most of the results appearing here were first established in , and . It should be noticed that this terminology is different from the notion of a dense subset in general topology. No topology is needed to define a dense submodule, and a dense submodule may or may not be topologically dense in a module with topology. Definition This article modifies exposition appearing in and . Let ''R'' be a ring, and ''M'' be a right ''R'' module with submodule ''N''. For an element ''y'' of ''M'', define :y^N=\ \, Note that the expression ''y''−1 is only formal since it is not meaningful to speak of the module-element ''y'' being invertible, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flat Cover
In algebra, a flat cover of a module ''M'' over a ring is a surjective homomorphism from a flat module ''F'' to ''M'' that is in some sense minimal. Any module over a ring has a flat cover that is unique up to (non-unique) isomorphism. Flat covers are in some sense dual to injective hulls, and are related to projective covers and torsion-free cover In algebra, a torsion-free module is a module over a ring such that zero is the only element annihilated by a regular element (non zero-divisor) of the ring. In other words, a module is ''torsion free'' if its torsion submodule is reduced to its ...s. Definitions The homomorphism ''F''→''M'' is defined to be a flat cover of ''M'' if it is surjective, ''F'' is flat, every homomorphism from flat module to ''M'' factors through ''F'', and any map from ''F'' to ''F'' commuting with the map to ''M'' is an automorphism of ''F''. History While projective covers for modules do not always exist, it was speculated that for general rings, ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grothendieck Category
In mathematics, a Grothendieck category is a certain kind of abelian category, introduced in Alexander Grothendieck's Tôhoku paper of 1957English translation in order to develop the machinery of homological algebra for modules and for sheaves in a unified manner. The theory of these categories was further developed in Pierre Gabriel's seminal thesis in 1962. To every algebraic variety V one can associate a Grothendieck category \operatorname(V), consisting of the quasi-coherent sheaves on V. This category encodes all the relevant geometric information about V, and V can be recovered from \operatorname(V) (the Gabriel–Rosenberg reconstruction theorem). This example gives rise to one approach to noncommutative algebraic geometry: the study of "non-commutative varieties" is then nothing but the study of (certain) Grothendieck categories. Definition By definition, a Grothendieck category \mathcal is an AB5 category with a generator. Spelled out, this means that * \mathcal is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enough Injectives
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of abelian groups, Ab. The theory originated in an effort to unify several cohomology theories by Alexander Grothendieck and independently in the slightly earlier work of David Buchsbaum. Abelian categories are very ''stable'' categories; for example they are regular and they satisfy the snake lemma. The class of abelian categories is closed under several categorical constructions, for example, the category of chain complexes of an abelian category, or the category of functors from a small category to an abelian category are abelian as well. These stability properties make them inevitable in homological algebra and beyond; the theory has major applications in algebraic geometry, cohomology and pure category theory. Abelian categories ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Small Category
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. '' Category theory'' is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Object (category Theory)
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. '' Category theory'' is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of abelian groups, Ab. The theory originated in an effort to unify several cohomology theories by Alexander Grothendieck and independently in the slightly earlier work of David Buchsbaum. Abelian categories are very ''stable'' categories; for example they are regular and they satisfy the snake lemma. The class of abelian categories is closed under several categorical constructions, for example, the category of chain complexes of an abelian category, or the category of functors from a small category to an abelian category are abelian as well. These stability properties make them inevitable in homological algebra and beyond; the theory has major applications in algebraic geometry, cohomology and pure category theory. Abelian categories ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indecomposable Module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules. Jacobson (2009), p. 111. Indecomposable is a weaker notion than simple module (which is also sometimes called irreducible module): simple means "no proper submodule" N < M, while indecomposable "not expressible as ". A direct sum of indecomposables is called completely decomposable; this is weaker than being semisimple, which is a direct sum of s. A direct sum decomposition of a module into indecomposable modules is called an |