|
Hereditarily Finite Sets
In mathematics and set theory, hereditarily finite sets are defined as finite sets whose elements are all hereditarily finite sets. In other words, the set itself is finite, and all of its elements are finite sets, recursively all the way down to the empty set. Formal definition A recursive definition of well-founded hereditarily finite sets is as follows: : ''Base case'': The empty set is a hereditarily finite set. : ''Recursion rule'': If ''a''1,...,''a''''k'' are hereditarily finite, then so is . The set \ is an example for such a hereditarily finite set and so is the empty set \emptyset=\. On the other hand, the sets \ or \ are examples of finite sets that are not ''hereditarily'' finite. For example, the first cannot be hereditarily finite since it contains at least one infinite set as an element, when = \. Discussion A symbol for the class of hereditarily finite sets is H_, standing for the cardinality of each of its member being smaller than \aleph_0. Whether H_ is a set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructive Set Theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with "=" and "\in" of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories. In addition to rejecting the principle of excluded middle (), constructive set theories often require some logical quantifiers in their axioms to be bounded, motivated by results tied to impredicativity. Introduction Constructive outlook Use of intuitionistic logic The logic of the set theories discussed here is constructive in that it rejects , i.e. that the disjunction \phi \lor \neg \phi automatically holds for all propositions. As a rule, to prove the excluded middle for a proposition P, i.e. to prove the particular disjunction P \lor \neg P, either P or \neg P needs to be explicitly prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tree (graph Theory)
In graph theory In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conne ..., a tree is an undirected graph in which any two Vertex (graph theory), vertices are connected by ''exactly one'' Path (graph theory), path, or equivalently a Connected graph, connected Cycle (graph theory), acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by ''at most one'' path, or equivalently an acyclic undirected graph, or equivalently a Disjoint union of graphs, disjoint union of trees. A polytreeSee . (or directed tree or oriented treeSee .See . or singly connected networkSee .) is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirecte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Set
In set theory, a branch of mathematics, a set A is called transitive if either of the following equivalent conditions hold: * whenever x \in A, and y \in x, then y \in A. * whenever x \in A, and x is not an urelement, then x is a subset of A. Similarly, a class M is transitive if every element of M is a subset of M. Examples Using the definition of ordinal numbers suggested by John von Neumann, ordinal numbers are defined as hereditarily transitive sets: an ordinal number is a transitive set whose members are also transitive (and thus ordinals). The class of all ordinals is a transitive class. Any of the stages V_\alpha and L_\alpha leading to the construction of the von Neumann universe V and Gödel's constructible universe L are transitive sets. The universes V and L themselves are transitive classes. This is a complete list of all finite transitive sets with up to 20 brackets: * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetration
In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though \uparrow \uparrow and the left-exponent ''xb'' are common. Under the definition as repeated exponentiation, means , where ' copies of ' are iterated via exponentiation, right-to-left, i.e. the application of exponentiation n-1 times. ' is called the "height" of the function, while ' is called the "base," analogous to exponentiation. It would be read as "the th tetration of ". It is the next hyperoperation after exponentiation, but before pentation. The word was coined by Reuben Louis Goodstein from tetra- (four) and iteration. Tetration is also defined recursively as : := \begin 1 &\textn=0, \\ a^ &\textn>0, \end allowing for attempts to extend tetration to non-natural numbers such as real and complex numbers. The two inverses of tetration are called super-root and super-logarithm, analogous to the nth root and the log ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinality
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set A = \ contains 3 elements, and therefore A has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set is also called its size, when no confusion with other notions of size is possible. The cardinality of a set A is usually denoted , A, , with a vertical bar on each side; this is the same notation as absolute value, and the meaning depends on context. The cardinality of a set A may alternatively be denoted by n(A), , \operatorname(A), or \#A. History A crude sense of cardinality, an awareness that groups of things or events compare with other grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countably
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (its number of elements) is not greater than that of the natural numbers. A countable set that is not finite is said countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined here are quite com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Set
In mathematics, the power set (or powerset) of a set is the set of all subsets of , including the empty set and itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is postulated by the axiom of power set. The powerset of is variously denoted as , , , \mathbb(S), or . The notation , meaning the set of all functions from S to a given set of two elements (e.g., ), is used because the powerset of can be identified with, equivalent to, or bijective to the set of all the functions from to the given two elements set. Any subset of is called a ''family of sets'' over . Example If is the set , then all the subsets of are * (also denoted \varnothing or \empty, the empty set or the null set) * * * * * * * and hence the power set of is . Properties If is a finite set with the cardinality (i.e., the number of all elements in the set is ), then the number of all the subsets of is . This fact as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Neumann Universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
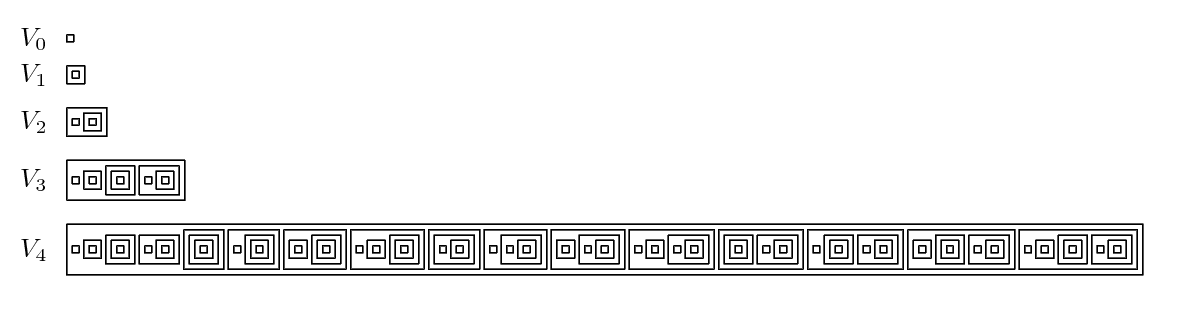
Nested Set V4
''Nested'' is the seventh studio album by Bronx-born singer, songwriter and pianist Laura Nyro, released in 1978 on Columbia Records. Following on from her extensive tour to promote 1976's ''Smile'', which resulted in the 1977 live album '' Season of Lights'', Nyro retreated to her new home in Danbury, Connecticut, where she lived after spending her time in the spotlight in New York City. Nyro had a studio built at her home, and recorded the songs that comprised ''Nested'' there. The songs deal with themes such as motherhood and womanhood, and it is a notably more relaxed Nyro that sings on the album. The instrumentation is laidback and smooth, similar to that of ''Smile'', but perhaps less jazz-inspired and more melodic. Nyro was assisted in production by Roscoe Harring, while Dale and Pop Ashby were chief engineers. Critics praised the album as a melodic return to form, and Nyro supported the album with a solo tour when she was heavily pregnant with her son Gil, who was born ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Of Infinity
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.Zermelo: ''Untersuchungen über die Grundlagen der Mengenlehre'', 1907, in: Mathematische Annalen 65 (1908), 261-281; Axiom des Unendlichen p. 266f. Formal statement In the formal language of the Zermelo–Fraenkel axioms, the axiom reads: :\exists \mathbf \, ( \empty \in \mathbf \, \land \, \forall x \in \mathbf \, ( \, ( x \cup \ ) \in \mathbf ) ) . In words, there is a set I (the set which is postulated to be infinite), such that the empty set is in I, and such that whenever any ''x'' is a member of I, the set formed by taking the union of ''x'' with its singleton is also a member of I. Such a set is sometimes called an inductive set. Inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |