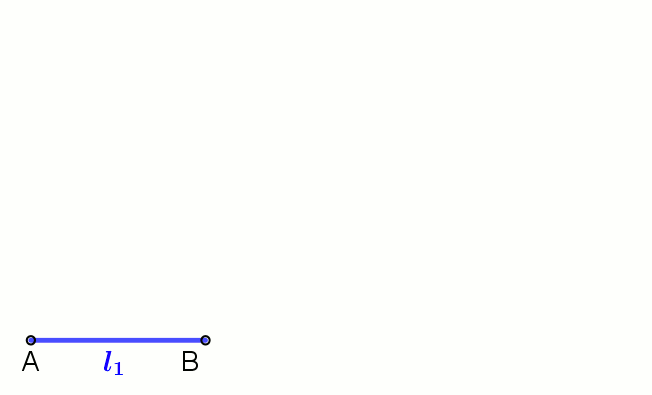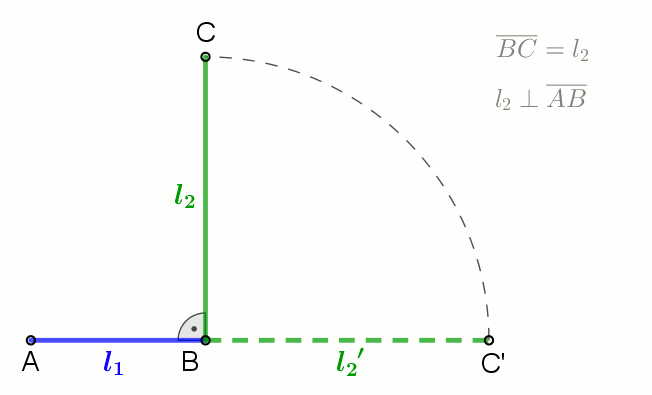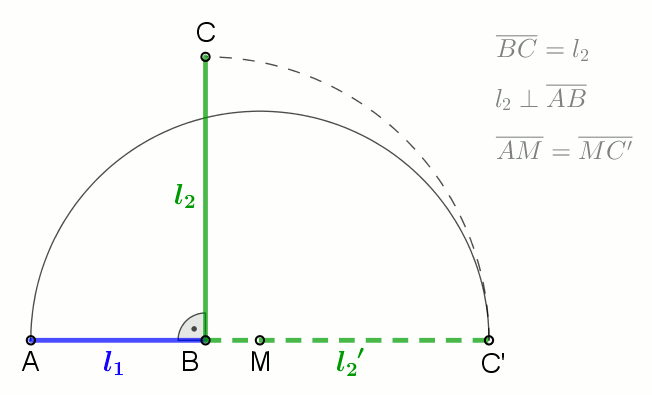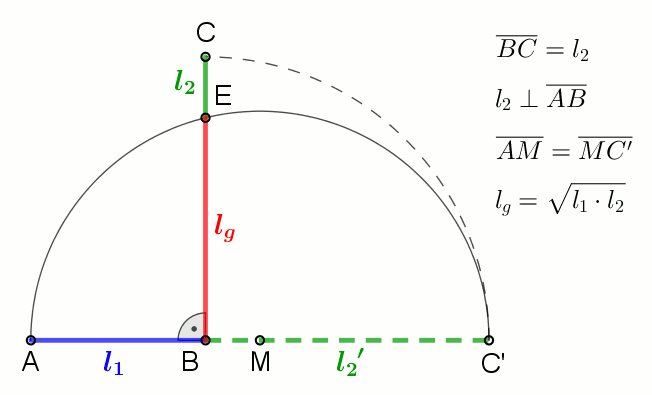|
Geometrical Properties Of Polynomial Roots
In mathematics, a univariate polynomial of degree with real or complex coefficients has complex zero of a function, roots, if counted with their multiplicities. They form a multiset of points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial. Some of these geometrical properties are related to a single polynomial, such as upper bounds on the absolute values of the roots, which define a disk containing all roots, or lower bounds on the distance between two roots. Such bounds are widely used for root-finding algorithms for polynomials, either for tuning them, or for computing their computational complexity. Some other properties are probabilistic, such as the expected number of real roots of a random polynomial of degree with real coefficients, which is less than 1+\frac 2\pi \ln (n) for sufficiently large. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He was one of the first to state and rigorously prove theorems of calculus, rejecting the heuristic principle of the generality of algebra of earlier authors. He almost singlehandedly founded complex analysis and the study of permutation groups in abstract algebra. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: "More concepts and theorems have been named for Cauchy than for any other mathematician (in Elasticity (physics), elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific writer; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Using Hölder's Inequality
Use may refer to: * Use (law), an obligation on a person to whom property has been conveyed * Use (liturgy), a special form of Roman Catholic ritual adopted for use in a particular diocese * Use–mention distinction, the distinction between using a word and mentioning it * Consumption (economics) ** Resource depletion, use to the point of lack of supply ** Psychological manipulation, in a form that treats a person is as a means to an end * Rental utilization, quantification of the use of assets to be continuously let See also * Use case * User story * USE (other) * Used (other) Used may refer to: Common meanings *Used good, goods of any type that have been used before or pre-owned *Used to, English auxiliary verb Places *Used, Huesca, a village in Huesca, Aragon, Spain *Used, Zaragoza, a town in Zaragoza, Aragon, Spain ... * User (other) {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mahler Measure
In mathematics, the Mahler measure M(p) of a polynomial p(z) with complex coefficients is defined as M(p) = , a, \prod_ , \alpha_i, = , a, \prod_^n \max\, where p(z) factorizes over the complex numbers \mathbb as p(z) = a(z-\alpha_1)(z-\alpha_2)\cdots(z-\alpha_n). The Mahler measure can be viewed as a kind of height function. Using Jensen's formula, it can be proved that this measure is also equal to the geometric mean of , p(z), for z on the unit circle (i.e., , z, = 1): M(p) = \exp\left(\int_^ \ln(, p(e^), )\, d\theta \right). By extension, the Mahler measure of an algebraic number \alpha is defined as the Mahler measure of the minimal polynomial of \alpha over \mathbb. In particular, if \alpha is a Pisot number or a Salem number, then its Mahler measure is simply \alpha. The Mahler measure is named after the German-born Australian mathematician Kurt Mahler. Properties * The Mahler measure is multiplicative: \forall p, q, \,\, M(p \cdot q) = M(p) \cdot M(q). * M(p) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edmund Landau
Edmund Georg Hermann Landau (14 February 1877 – 19 February 1938) was a German mathematician who worked in the fields of number theory and complex analysis. Biography Edmund Landau was born to a Jewish family in Berlin. His father was Leopold Landau, a gynecologist and his mother was Johanna Jacoby. Landau studied mathematics at the University of Berlin, receiving his doctorate in 1899 and his habilitation (the post-doctoral qualification required to teach in German universities) in 1901. His doctoral thesis was 14 pages long. In 1895, his paper on scoring chess tournaments is the earliest use of eigenvector centrality. Landau taught at the University of Berlin from 1899 to 1909, after which he held a chair at the University of Göttingen. He married Marianne Ehrlich, the daughter of the Nobel Prize-winning biologist Paul Ehrlich, in 1905. At the 1912 International Congress of Mathematicians Landau listed four problems in number theory about primes that he said were parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tohoku Mathematical Journal
The ''Tohoku Mathematical Journal'' is a mathematical research journal published by Tohoku University in Japan. It was founded in August 1911 by Tsuruichi Hayashi. History Due to World War II the publication of the journal stopped in 1943 with volume 49. Publication was resumed in 1949 with the volume numbering starting again at 1. In order to distinguish between the identical numbered volumes, volumes in the first publishing period are referred to as the ''first series'' whereas the later volumes are called ''second series''. Before volume 51 of the second series the journal was called ''Tôhoku Mathematical Journal'', with a circumflex over the second letter of ''Tohoku''. Selected papers *. The first publication of the Sprague–Grundy theorem, the basis for much of combinatorial game theory, later independently rediscovered by P. M. Grundy. *. This paper describes Weiszfeld's algorithm for finding the geometric median. *. This paper, often referred to as " The Tohoku pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the ''common ratio''. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2. Examples of a geometric sequence are powers ''r''''k'' of a fixed non-zero number ''r'', such as 2''k'' and 3''k''. The general form of a geometric sequence is :a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots where ''r'' ≠ 0 is the common ratio and ''a'' ≠ 0 is a scale factor, equal to the sequence's start value. The sum of a geometric progression terms is called a ''geometric series''. Elementary properties The ''n''-th term of a geometric sequence with initial value ''a'' = ''a''1 and common ratio ''r'' is given by :a_n = a\,r^, and in general :a_n = a_m\,r^. Such a geometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-norm
In mathematics, the spaces are function spaces defined using a natural generalization of the -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Applications Statistics In statistics, measures of central tendency and statistical dispersion, such as the mean, median, and standard deviation, are defined in terms of metrics, and measures of central tendency can be characterized as solutions to variational problems. In penalized regression, "L1 penalty" and "L2 penalty" refer to penaliz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hölder's Inequality
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of spaces. :Theorem (Hölder's inequality). Let be a measure space and let with . Then for all measurable real number, real- or complex number, complex-valued function (mathematics), functions and on , ::\, fg\, _1 \le \, f\, _p \, g\, _q. :If, in addition, and and , then Hölder's inequality becomes an equality if and only if and are Linear dependence, linearly dependent in , meaning that there exist real numbers , not both of them zero, such that -almost everywhere. The numbers and above are said to be Hölder conjugates of each other. The special case gives a form of the Cauchy–Schwarz inequality. Hölder's inequality holds even if is infinite, the right-hand side also being infinite in that case. Conversely, if is in and is in , then the pointwise product is in . Hölder's inequality is used to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donald Knuth
Donald Ervin Knuth ( ; born January 10, 1938) is an American computer scientist, mathematician, and professor emeritus at Stanford University. He is the 1974 recipient of the ACM Turing Award, informally considered the Nobel Prize of computer science. Knuth has been called the "father of the analysis of algorithms". He is the author of the multi-volume work ''The Art of Computer Programming'' and contributed to the development of the rigorous analysis of the computational complexity of algorithms and systematized formal mathematical techniques for it. In the process, he also popularized the asymptotic notation. In addition to fundamental contributions in several branches of theoretical computer science, Knuth is the creator of the TeX computer typesetting system, the related METAFONT font definition language and rendering system, and the Computer Modern family of typefaces. As a writer and scholar, Knuth created the WEB and CWEB computer programming systems designed to encou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transpose
In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley. In the case of a logical matrix representing a binary relation R, the transpose corresponds to the converse relation RT. Transpose of a matrix Definition The transpose of a matrix , denoted by , , , A^, , , or , may be constructed by any one of the following methods: # Reflect over its main diagonal (which runs from top-left to bottom-right) to obtain #Write the rows of as the columns of #Write the columns of as the rows of Formally, the -th row, -th column element of is the -th row, -th column element of : :\left mathbf^\operatorname\right = \left mathbf\right. If is an matrix, then is an matrix. In the case of square matrices, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |