|
Geometric Progression
A geometric progression, also known as a geometric sequence, is a mathematical sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed number called the ''common ratio''. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with a common ratio of 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with a common ratio of 1/2. Examples of a geometric sequence are powers ''r''''k'' of a fixed non-zero number ''r'', such as 2''k'' and 3''k''. The general form of a geometric sequence is :a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots where ''r'' is the common ratio and ''a'' is the initial value. The sum of a geometric progression's terms is called a '' geometric series''. Properties The ''n''th term of a geometric sequence with initial value ''a'' = ''a''1 and common ratio ''r'' is given by :a_n = a\,r^, and in general :a_n = a_m\,r^. Geometric sequences satisfy the linear recurrence relation :a_n = r\,a_ f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
An Essay On The Principle Of Population
The book ''An Essay on the Principle of Population'' was first published anonymously in 1798, but the author was soon identified as Thomas Robert Malthus. The book warned of future difficulties, on an interpretation of the population increasing in geometric progression (so as to double every 25 years) while food production increased in an arithmetic progression, which would leave a difference resulting in the want of food and famine, unless birth rates decreased. While it was not the first book on population, Malthus's book fuelled debate about the size of the population in Britain and contributed to the passing of the Census Act 1800. This Act enabled the holding of a national census in England, Wales and Scotland, starting in 1801 and continuing every ten years to the present. The book's 6th edition (1826) was independently cited as a key influence by both Charles Darwin and Alfred Russel Wallace in developing the theory of natural selection. A key portion of the book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonian Mathematics
Babylonian mathematics (also known as Assyro-Babylonian mathematics) is the mathematics developed or practiced by the people of Mesopotamia, as attested by sources mainly surviving from the Old Babylonian period (1830–1531 BC) to the Seleucid from the last three or four centuries BC. With respect to content, there is scarcely any difference between the two groups of texts. Babylonian mathematics remained constant, in character and content, for over a millennium. In contrast to the scarcity of sources in Egyptian mathematics, knowledge of Babylonian mathematics is derived from hundreds of clay tablets unearthed since the 1850s. Written in cuneiform, tablets were inscribed while the clay was moist, and baked hard in an oven or by the heat of the sun. The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics that include fractions, algebra, quadratic and cubic equations and the Pythagorean theorem. The Babylonian tablet YBC 7289 gives an approxim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shuruppak
Shuruppak ( , SU.KUR.RUki, "the healing place"), modern Tell Fara, was an ancient Sumerian city situated about 55 kilometres (35 mi) south of Nippur and 30 kilometers north of ancient Uruk on the banks of the Euphrates in Iraq's Al-Qādisiyyah Governorate. Shuruppak was dedicated to Ninlil, also called Sud, the goddess of grain and the air. The Early Dynastic IIIa period is also sometimes called the Fara period. Not to be confused with the Levantine archaeological site Tell el-Far'ah (South). "Shuruppak" is sometimes also the name of a king of the city, legendary survivor of Flood story, the Flood, and supposed author of the Instructions of Shuruppak". History Jemdet Nasr period The earliest excavated levels at Shuruppak date to the Jemdet Nasr period about 3000 BC. Several objects made of arsenical copper were found in Shuruppak/Fara dating to the Jemdet Nasr period (c. 2900 BC). Similar objects were also found at Tepe Gawra (levels XII-VIII). Early Dynastic II The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sumer
Sumer () is the earliest known civilization, located in the historical region of southern Mesopotamia (now south-central Iraq), emerging during the Chalcolithic and Early Bronze Age, early Bronze Ages between the sixth and fifth millennium BC. Like nearby Elam, it is one of the Cradle of civilization, cradles of civilization, along with ancient Egypt, Egypt, the Indus Valley Civilisation, Indus Valley, the Erligang culture of the Yellow River valley, Caral-Supe civilization, Caral-Supe, and Mesoamerica. Living along the valleys of the Tigris and Euphrates rivers, Sumerian farmers grew an abundance of grain and other crops, a surplus of which enabled them to form urban settlements. The world's earliest known texts come from the Sumerian cities of Uruk and Jemdet Nasr, and date to between , following a period of proto-writing . Name The term "Sumer" () comes from the Akkadian Empire, Akkadian name for the "Sumerians", the ancient non-Semitic languages, Semitic-speaking inhabitan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Early Dynastic Period (Mesopotamia)
The Early Dynastic Period (abbreviated ED Period or ED) is an archaeological culture in Mesopotamia (modern-day Iraq) that is generally dated to and was preceded by the Uruk and Jemdet Nasr periods. It saw the development of writing and the formation of the first cities and states. The ED itself was characterized by the existence of multiple city-states: small states with a relatively simple structure that developed and solidified over time. This development ultimately led, directly after this period, to broad Mesopotamian unification under the rule of Sargon, the first monarch of the Akkadian Empire. Despite their political fragmentation, the ED city-states shared a relatively homogeneous material culture. Sumerian cities such as Uruk, Ur, Lagash, Umma, and Nippur located in Lower Mesopotamia were very powerful and influential. To the north and west stretched states centered on cities such as Kish, Mari, Nagar, and Ebla. The study of Central and Lower Mesopotamia has l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ), arithmetic average, or just the ''mean'' or ''average'' is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results from an experiment, an observational study, or a Survey (statistics), survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics because it helps to distinguish it from other types of means, such as geometric mean, geometric and harmonic mean, harmonic. Arithmetic means are also frequently used in economics, anthropology, history, and almost every other academic field to some extent. For example, per capita income is the arithmetic average of the income of a nation's Human population, population. While the arithmetic mean is often used to report central tendency, central tendencies, it is not a robust statistic: it is greatly influenced by outliers (Value (mathematics), values much larger or smaller than ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Sequence
An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference from any succeeding term to its preceding term remains constant throughout the sequence. The constant difference is called common difference of that arithmetic progression. For instance, the sequence 5, 7, 9, 11, 13, 15, . . . is an arithmetic progression with a common difference of 2. If the initial term of an arithmetic progression is a_1 and the common difference of successive members is d, then the n-th term of the sequence (a_n) is given by :a_n = a_1 + (n - 1)d. A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression. The sum of a finite arithmetic progression is called an arithmetic series. History According to an anecdote of uncertain reliability, in primary school Carl Friedrich Gauss reinvented the formula \tfrac for summing the integers from 1 through n, for the case n=100, by grouping t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite collection of positive real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean of numbers is the Nth root, th root of their product (mathematics), product, i.e., for a collection of numbers , the geometric mean is defined as : \sqrt[n]. When the collection of numbers and their geometric mean are plotted in logarithmic scale, the geometric mean is transformed into an arithmetic mean, so the geometric mean can equivalently be calculated by taking the natural logarithm of each number, finding the arithmetic mean of the logarithms, and then returning the result to linear scale using the exponential function , :\sqrt[n] = \exp \left( \frac \right). The geometric mean of two numbers is the square root of their product, for example with numbers and the geometric mean is \textstyle \sqrt = The geometric mean o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Progression Sum Visual Proof
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
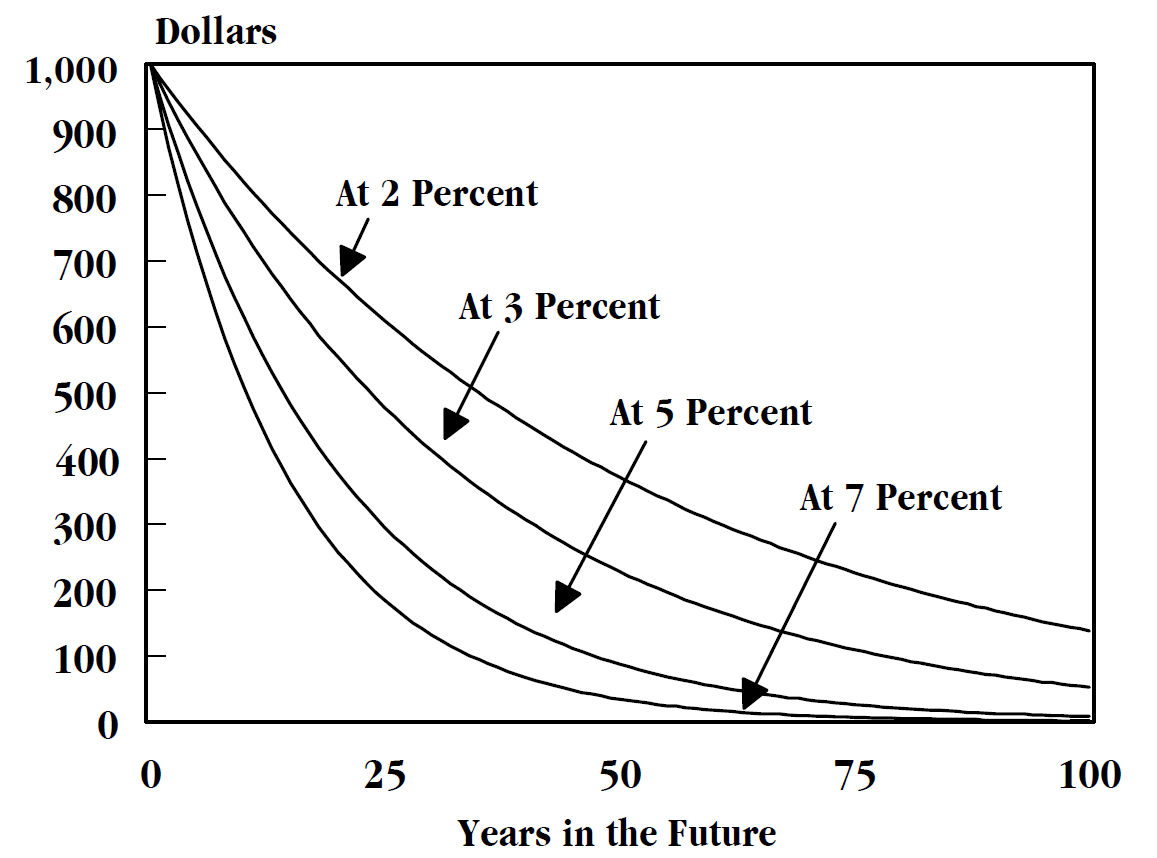
Time Value Of Money
The time value of money refers to the fact that there is normally a greater benefit to receiving a sum of money now rather than an identical sum later. It may be seen as an implication of the later-developed concept of time preference. The time value of money refers to the observation that it is better to receive money sooner than later. Money you have today can be invested to earn a positive rate of return, producing more money tomorrow. Therefore, a dollar today is worth more than a dollar in the future. The time value of money is among the factors considered when weighing the opportunity costs of spending rather than saving or investing money. As such, it is among the reasons why interest is paid or earned: interest, whether it is on a bank deposit or debt, compensates the depositor or lender for the loss of their use of their money. Investors are willing to forgo spending their money now only if they expect a favorable net rate of return, return on their investment in the fut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prosthaphaeresis
Prosthaphaeresis (from the Greek ''προσθαφαίρεσις'') was an algorithm used in the late 16th century and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm in 1614, it was the only known generally applicable way of approximating products quickly. Its name comes from the Greek ''prosthen'' (πρόσθεν) meaning before and ''aphaeresis'' (ἀφαίρεσις), meaning taking away or subtraction. In ancient times the term was used to mean a reduction to bring the apparent place of a moving point or planet to the mean place (see Equation of the center). Nicholas Copernicus mentions "prosthaphaeresis" several times in his 1543 work , to mean the "great parallax" caused by the displacement of the observer due to the Earth's annual motion. History and motivation In 16th-century Europe, celestial navigation of ships on long voyages relied heavily on ephemerides to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |