|
Gyroelongated Square Pyramid
In geometry, the gyroelongated square pyramid is one of the Johnson solids (). As its name suggests, it can be constructed by taking a square pyramid and "gyroelongating" it, which in this case involves joining a square antiprism to its base. Applications The ''Gyroelongated square pyramid'' represents the capped square antiprismatic molecular geometry: : Dual polyhedron The dual of the gyroelongated square pyramid has 9 faces: 4 kites, 1 square and 4 pentagonal. See also * Gyroelongated square bipyramid In geometry, the gyroelongated square bipyramid, heccaidecadeltahedron, or tetrakis square antiprism is one of the Johnson solids (). As the name suggests, it can be constructed by gyroelongating an octahedron (square bipyramid) by inserting a s ... External links * Johnson solids Pyramids and bipyramids {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ( ); it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform (i.e., not Platonic solid, Archimedean solid, uniform prism, or uniform antiprism) before they refer to it as a “Johnson solid”. As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid () is an example that has a degree-5 vertex. Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the face ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Pyramid
In geometry, the elongated pentagonal pyramid is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal pyramid () by attaching a pentagonal prism to its base. Formulae The following formulae for the height (H), surface area (A) and volume (V) can be used if all faces are regular, with edge length L: :H = L\cdot \left( 1 + \sqrt\right) \approx L\cdot 1.525731112 :A = L^2 \cdot \frac \approx L^2\cdot 8.88554091 :V = L^3 \cdot \left( \frac \right) \approx L^3\cdot 2.021980233 Dual polyhedron The dual of the elongated pentagonal pyramid has 11 faces: 5 triangular, 1 pentagonal and 5 trapezoidal. It is topologically identical to the Johnson solid. See also * Elongated pentagonal bipyramid In geometry, the elongated pentagonal bipyramid or pentakis pentagonal prism is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal bipyramid () by inserting a pentagonal prism between ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Pentagonal Pyramid
In geometry, the gyroelongated pentagonal pyramid is one of the Johnson solids (). As its name suggests, it is formed by taking a pentagonal pyramid and "gyroelongating" it, which in this case involves joining a pentagonal antiprism to its base. It can also be seen as a diminished icosahedron, an icosahedron with the top (a pentagonal pyramid, ) chopped off by a plane. Other Johnson solids can be formed by cutting off multiple pentagonal pyramids from an icosahedron: the pentagonal antiprism and metabidiminished icosahedron (two pyramids removed), and the tridiminished icosahedron In geometry, the tridiminished icosahedron is one of the Johnson solids (). The name refers to one way of constructing it, by removing three pentagonal pyramids () from a regular icosahedron, which replaces three sets of five triangular faces fro ... (three pyramids removed). Dual polyhedron The dual of the gyroelongated pentagonal pyramid has 11 faces: 5 kites, 1 regular pentagonal and 5 irregu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non- collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (geometry)
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Symmetries
In three dimensional geometry, there are four infinite series of point groups in three dimensions (''n''≥1) with ''n''-fold rotational or reflectional symmetry about one axis (by an angle of 360°/''n'') that does not change the object. They are the finite symmetry groups on a cone. For ''n'' = ∞ they correspond to four frieze groups. Schönflies notation is used. The terms horizontal (h) and vertical (v) imply the existence and direction of reflections with respect to a vertical axis of symmetry. Also shown are Coxeter notation in brackets, and, in parentheses, orbifold notation. Types ;Chiral: *''Cn'', sup>+, (''nn'') of order ''n'' - ''n''-fold rotational symmetry - acro-n-gonal group (abstract group ''Zn''); for ''n''=1: no symmetry ( trivial group) ;Achiral: *''Cnh'', +,2 (''n''*) of order 2''n'' - prismatic symmetry or ortho-n-gonal group (abstract group ''Zn'' × ''Dih1''); for ''n''=1 this is denoted by ''Cs'' (1*) and called reflection symmetry, also bila ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid, the Johnson solid General square pyramid A possibly oblique square pyramid with base length ''l'' and perpendicular height ''h'' has volume: :V=\frac l^2 h. Right square pyramid In a right square pyramid, all the lateral edges have the same length, and the sides other than the base are congruent isosceles triangles. A right square pyramid with base length ''l'' and height ''h'' has surface area and volume: :A=l^2+l\sqrt, :V=\frac l^2 h. The lateral edge length is: :\sqrt; the slant height is: :\sqrt. The dihedral angles are: :*between the base and a side: :::\arctan \left(\right); :*between two sides: :::\arccos \left(\right). Equilateral square pyramid, Johnson solid J1 If all edges have the same length, then the sides are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Antiprism
In geometry, the square antiprism is the second in an infinite family of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an ''anticube''. If all its faces are regular, it is a semiregular polyhedron or uniform polyhedron. A nonuniform ''D''4-symmetric variant is the cell of the noble square antiprismatic 72-cell. Points on a sphere When eight points are distributed on the surface of a sphere with the aim of maximising the distance between them in some sense, the resulting shape corresponds to a square antiprism rather than a cube. Specific methods of distributing the points include, for example, the Thomson problem (minimizing the sum of all the reciprocals of distances between points), maximising the distance of each point to the nearest point, or minimising the sum of all reciprocals of squares of distances between points. Molecules with square antiprismatic geometry According to the VSEPR theory of molec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
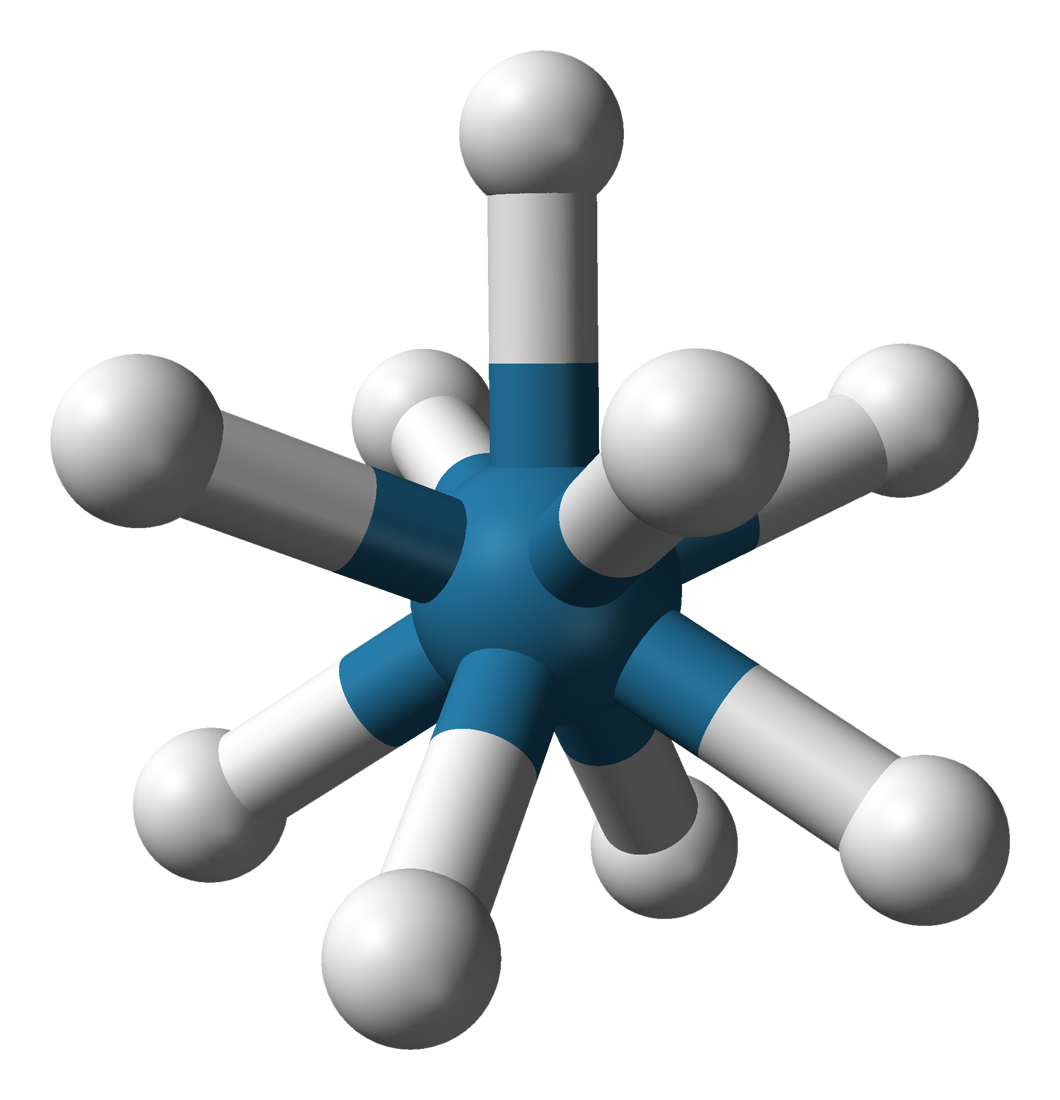
Capped Square Antiprismatic Molecular Geometry
In chemistry, the capped square antiprismatic molecular geometry describes the shape of compounds where nine atoms, groups of atoms, or ligands are arranged around a central atom, defining the vertices of a gyroelongated square pyramid. The gyroelongated square pyramid is a square pyramid with a square antiprism connected to the square base. In this respect, it can be seen as a "capped" square antiprism (a square antiprism with a pyramid erected on one of the square faces). It is very similar to the tricapped trigonal prismatic molecular geometry In chemistry, the tricapped trigonal prismatic molecular geometry describes the shape of compounds where nine atoms, groups of atoms, or ligands are arranged around a central atom, defining the vertices of a triaugmented triangular prism (a trig ..., and there is some dispute over the specific geometry exhibited by certain molecules. Examples * is sometimes described as having a capped square antiprismatic geometry, although its ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |