|
Gnomonics
Gnomonics (from the ancient Greek word γνώμων, , meaning 'interpreter, discerner') is the study of the design, construction and use of sundials. The foundations of gnomonics were known to the ancient Greek Anaximander (ca. 550 BCE), which augmented the science of shadows brought back from Egypt by Thales of Miletus. Gnomonics was used by Greek and Roman architects from 25 BCE for the design of buildings. Modern gnomonics has its root in the nascent European astronomy of the 16th Century. The first works, in Latin, were published by Sebastian Münster in 1531 and Oronce Fine in 1532, rapidly followed by books in French. At the end of the 17th century, gnomonics developed notably in the application of spherical trigonometry. Several methods, both graphical and analytical, were published in books which allowed the creation of sundials of greater or lesser precision to be placed on buildings and in gardens. In his ''Histoire de la Gnomonique ancienne et moderne'', Jean-Étienn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sundials
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat plate (the ''dial'') and a gnomon, which casts a shadow onto the dial. As the Sun appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The ''style'' is the time-telling edge of the gnomon, though a single point or ''nodus'' may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be parallel to the axis of the Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical latitude. The term ''sundial'' can refer to any device that uses the Sun's altitude or azimuth ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic period (), and the Classical period (). Ancient Greek was the language of Homer and of fifth-century Athenian historians, playwrights, and philosophers. It has contributed many words to English vocabulary and has been a standard subject of study in educational institutions of the Western world since the Renaissance. This article primarily contains information about the Epic and Classical periods of the language. From the Hellenistic period (), Ancient Greek was followed by Koine Greek, which is regarded as a separate historical stage, although its earliest form closely resembles Attic Greek and its latest form approaches Medieval Greek. There were several regional dialects of Ancient Greek, of which Attic Greek developed into Koine. Dia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
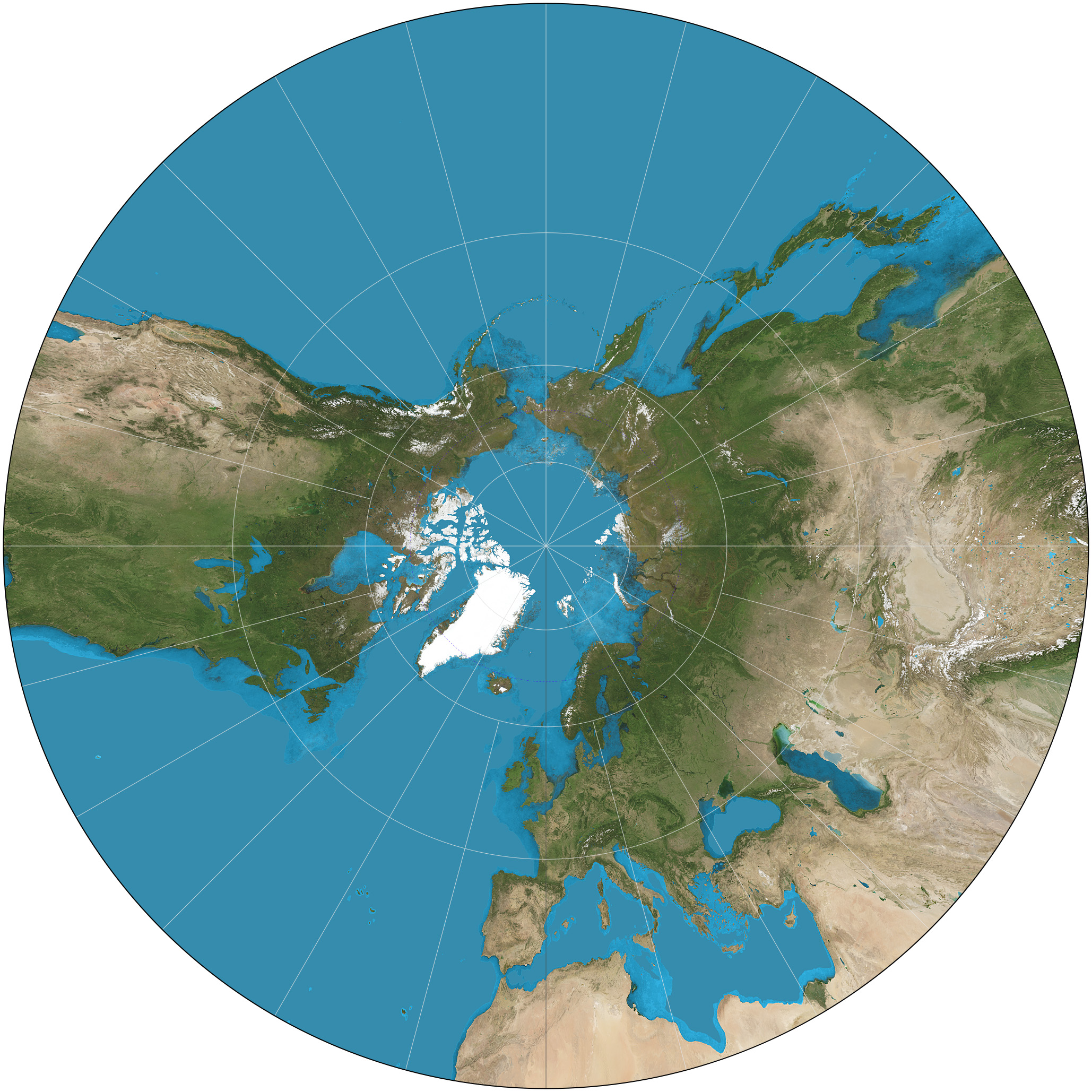
Gnomonic Projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map. Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees. History The gnomonic projection is said to be the oldest map projection, developed by Thales for star maps in the 6th century BC. The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map. Properties Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
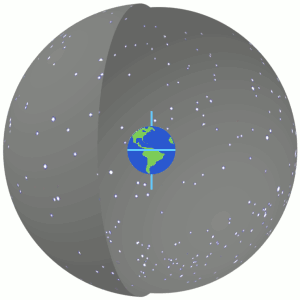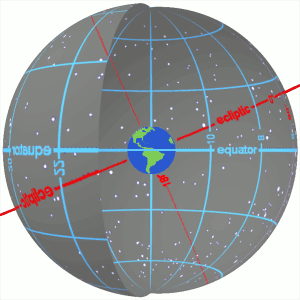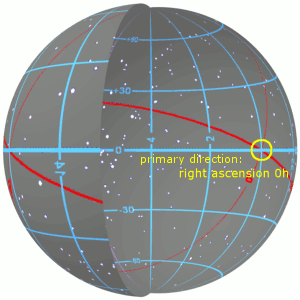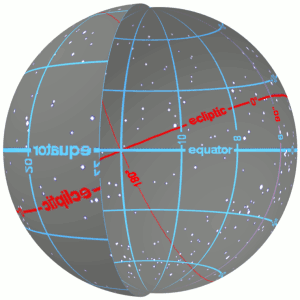
Declination
In astronomy, declination (abbreviated dec; symbol ''δ'') is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. Declination's angle is measured north or south of the celestial equator, along the hour circle passing through the point in question. The root of the word ''declination'' (Latin, ''declinatio'') means "a bending away" or "a bending down". It comes from the same root as the words ''incline'' ("bend foward") and ''recline'' ("bend backward"). In some 18th and 19th century astronomical texts, declination is given as ''North Pole Distance'' (N.P.D.), which is equivalent to 90 – (declination). For instance an object marked as declination −5 would have an N.P.D. of 95, and a declination of −90 (the south celestial pole) would have an N.P.D. of 180. Explanation Declination in astronomy is comparable to geographic latitude, projected onto the celestial sphere, and right ascension is like ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Transform
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If is the point set of an affine space, then every affine transformation on can be repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ecliptic Longitude
The ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets (except Mercury) and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the vernal (March) equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates. Primary direction The celestial equator and the ecliptic are slowly moving due to perturbing forces on the Earth, therefore the orientation of the primary direction, their intersection at the Northern Hemisphere vernal equinox, is not quite fixed. A slow motion of Earth's axis, precession, causes a slow, continuous turning of the coordinate system westward about the poles of the ecliptic, complet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
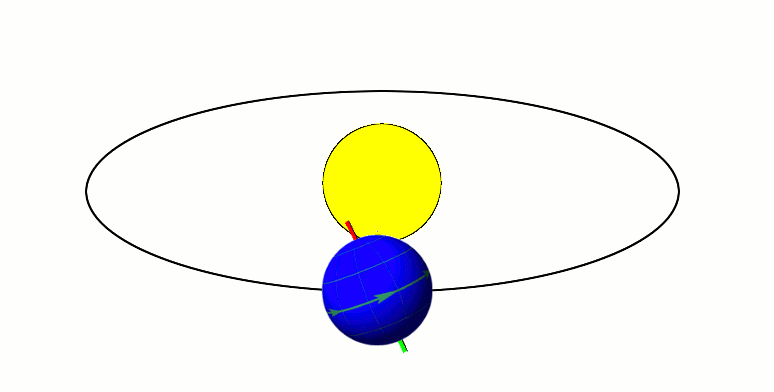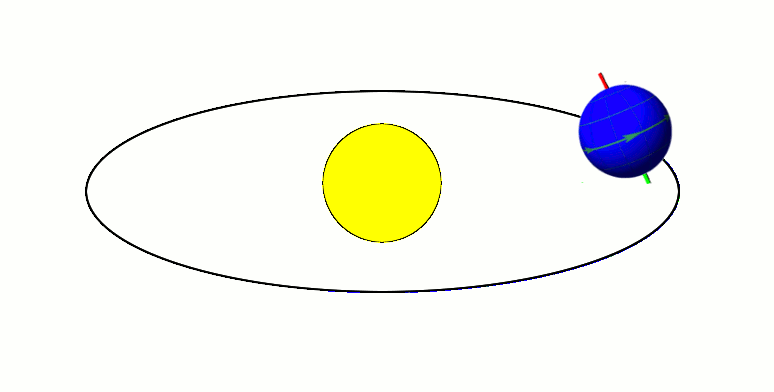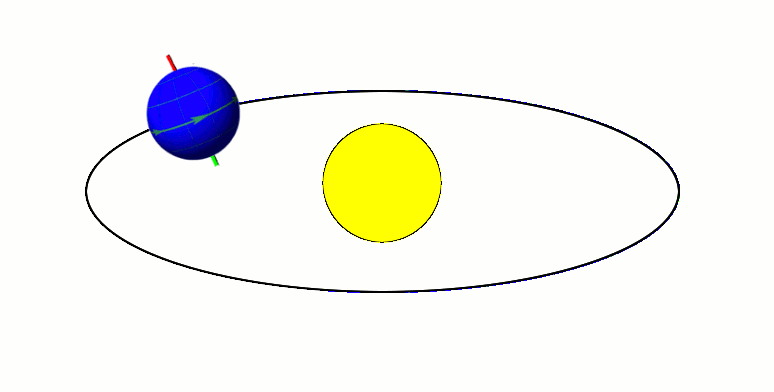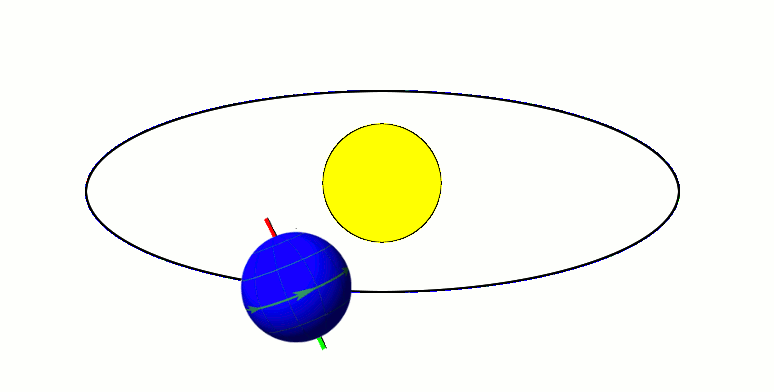
Axial Tilt
In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, which is the line perpendicular to its orbital plane; equivalently, it is the angle between its equatorial plane and orbital plane. It differs from orbital inclination. At an obliquity of 0 degrees, the two axes point in the same direction; that is, the rotational axis is perpendicular to the orbital plane. The rotational axis of Earth, for example, is the imaginary line that passes through both the North Pole and South Pole, whereas the Earth's orbital axis is the line perpendicular to the imaginary plane through which the Earth moves as it revolves around the Sun; the Earth's obliquity or axial tilt is the angle between these two lines. Earth's obliquity oscillates between 22.1 and 24.5 degrees on a 41,000-year cycle. Based on a continuously updated formula (here Laskar, 1986, though since 2006 the IMCCE and the IAU recommend the P03 model), Earth's mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sidereal Time
Sidereal time (as a unit also sidereal day or sidereal rotation period) (sidereal ) is a timekeeping system that astronomers use to locate celestial objects. Using sidereal time, it is possible to easily point a telescope to the proper coordinates in the night sky. In short, sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars", or more correctly, relative to the March equinox. Viewed from the same location, a star seen at one position in the sky will be seen at the same position on another night at the same sidereal time. This is similar to how the time kept by a sundial (Solar time) can be used to find the location of the Sun. Just as the Sun and Moon appear to rise in the east and set in the west due to the rotation of Earth, so do the stars. Both Solar time and sidereal time make use of the regularity of Earth's rotation about its polar axis: solar time following the Sun while, roughly speaking, sidereal time follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or ''normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the ocean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (mathematics)
In mathematics and physics, vector is a term that refers colloquially to some quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences of numbers of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a Euclidean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Change Of Basis
In mathematics, an ordered basis of a vector space of finite dimension allows representing uniquely any element of the vector space by a coordinate vector, which is a sequence of scalars called coordinates. If two different bases are considered, the coordinate vector that represents a vector on one basis is, in general, different from the coordinate vector that represents on the other basis. A change of basis consists of converting every assertion expressed in terms of coordinates relative to one basis into an assertion expressed in terms of coordinates relative to the other basis. Such a conversion results from the ''change-of-basis formula'' which expresses the coordinates relative to one basis in terms of coordinates relative to the other basis. Using matrices, this formula can be written :\mathbf x_\mathrm = A \,\mathbf x_\mathrm, where "old" and "new" refer respectively to the firstly defined basis and the other basis, \mathbf x_\mathrm and \mathbf x_\mathrm are the colu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |