|
Expander Mixing Lemma
The expander mixing lemma intuitively states that the edges of certain d-regular graphs are evenly distributed throughout the graph. In particular, the number of edges between two vertex subsets S and T is always close to the expected number of edges between them in a random d-regular graph, namely \frac dn, S, , T, . ''d''-Regular Expander Graphs Define an (n, d, \lambda)-graph to be a d-regular graph G on n vertices such that all of the eigenvalues of its adjacency matrix A_G except one have absolute value at most \lambda. The d-regularity of the graph guarantees that its largest absolute value of an eigenvalue is d. In fact, the all-1's vector \mathbf1 is an eigenvector of A_G with eigenvalue d, and the eigenvalues of the adjacency matrix will never exceed the maximum degree of G in absolute value. If we fix d and \lambda then (n, d, \lambda)-graphs form a family of expander graphs with a constant spectral gap. Statement Let G = (V, E) be an (n, d, \lambda)-graph. For any tw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expander Graph
In graph theory, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes. Definitions Intuitively, an expander graph is a finite, undirected multigraph in which every subset of the vertices that is not "too large" has a "large" boundary. Different formalisations of these notions give rise to different notions of expanders: ''edge expanders'', ''vertex expanders'', and ''spectral expanders'', as defined below. A disconnected graph is not an expander, since the boundary of a connected component is empty. Every connected graph is an expander; however, different connected graphs have different expansion parameters. The complete graph has the best expansion property, but it has largest possible degree. Informal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Graph
In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of ''typical'' graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, ''random graph'' refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a ''random graph''. Models A random graph is obtained by starting with a set of ''n'' isolated vertices and adding successive edges between them at random. The aim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree is called a graph or regular graph of degree . Also, from the handshaking lemma, a regular graph contains an even number of vertices with odd degree. Regular graphs of degree at most 2 are easy to classify: a graph consists of disconnected vertices, a graph consists of disconnected edges, and a graph consists of a disjoint union of cycles and infinite chains. A graph is known as a cubic graph. A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number of neighbors in common, and every non-adjacent pair of vertices has the same number of neighbors in common. The smallest graphs that are regular but not strong ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex. Definition For a simple graph with vertex set , the adjacency matrix is a square matrix such that its element is one when there is an edge from vertex to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expander Graph
In graph theory, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes. Definitions Intuitively, an expander graph is a finite, undirected multigraph in which every subset of the vertices that is not "too large" has a "large" boundary. Different formalisations of these notions give rise to different notions of expanders: ''edge expanders'', ''vertex expanders'', and ''spectral expanders'', as defined below. A disconnected graph is not an expander, since the boundary of a connected component is empty. Every connected graph is an expander; however, different connected graphs have different expansion parameters. The complete graph has the best expansion property, but it has largest possible degree. Informal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Gap
In mathematics, the spectral gap is the difference between the moduli of the two largest eigenvalues of a matrix or operator; alternately, it is sometimes taken as the smallest non-zero eigenvalue. Various theorems relate this difference to other properties of the system. See also * Cheeger constant (graph theory) * Cheeger constant (Riemannian geometry) * Eigengap * Spectral gap (physics) * Spectral radius In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectru ... References External links * {{Mathanalysis-stub Spectral theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biregular Graph
In graph-theoretic mathematics, a biregular graph or semiregular bipartite graph is a bipartite graph G=(U,V,E) for which every two vertices on the same side of the given bipartition have the same degree as each other. If the degree of the vertices in U is x and the degree of the vertices in V is y, then the graph is said to be (x,y)-biregular. Example Every complete bipartite graph K_ is (b,a)-biregular. The rhombic dodecahedron is another example; it is (3,4)-biregular. Vertex counts An (x,y)-biregular graph G=(U,V,E) must satisfy the equation x, U, =y, V, . This follows from a simple double counting argument: the number of endpoints of edges in U is x, U, , the number of endpoints of edges in V is y, V, , and each edge contributes the same amount (one) to both numbers. Symmetry Every regular bipartite graph is also biregular. Every edge-transitive graph (disallowing graphs with isolated vertices) that is not also vertex-transitive must be biregular.. In particular every e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. The two sets U and V may be thought of as a coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another red, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color. One often writes G=(U,V,E) to denote a bipartite graph whose partition has the parts U and V, with E denoting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex. Definition For a simple graph with vertex set , the adjacency matrix is a square matrix such that its element is one when there is an edge from vertex to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
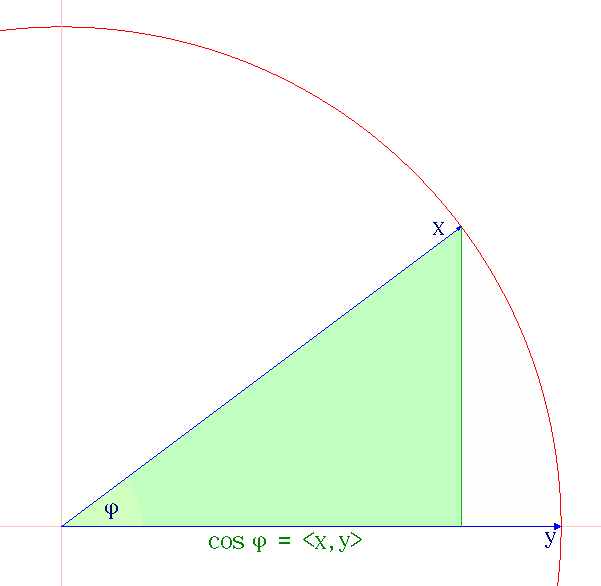
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-negative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as-is. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus ''any'' two distinct lines in a projective plane intersect at exactly one point. Renaissance artists, in developing the techniques of drawing in perspective, laid the groundwork for this mathematical topic. The archetypical example is the real projective plane, also known as the extended Euclidean plane. This example, in slightly different guises, is important in algebraic geometry, topology and projective geometry where it may be denoted variously by , RP2, or P2(R), among other notations. There are many other projective planes, both infinite, such as the complex projective plane, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
