|
Combinatorial Group Theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations. It is much used in geometric topology, the fundamental group of a simplicial complex having in a natural and geometric way such a presentation. A very closely related topic is geometric group theory, which today largely subsumes combinatorial group theory, using techniques from outside combinatorics besides. It also comprises a number of algorithmically insoluble problems, most notably the word problem for groups; and the classical Burnside problem. History See for a detailed history of combinatorial group theory. A proto-form is found in the 1856 icosian calculus of William Rowan Hamilton, where he studied the icosahedral symmetry group via the edge graph of the dodecahedron. The foundations of combinatorial group theory were laid by Walther von Dyck, student of Felix Klein Christian Felix Klein (; 25 April 1849 – 22 Ju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Problem For Groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group ''G'' is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if ''A'' is a finite set of generators for ''G'' then the word problem is the membership problem for the formal language of all words in ''A'' and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on ''A'' to the group ''G''. If ''B'' is another finite generating set for ''G'', then the word problem over the generating set ''B'' is equivalent to the word problem over the generating set ''A''. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group ''G''. The related but different uniform word problem for a class ''K'' of recursively presented groups is the algorithmic problem of deciding, given as input a pres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Walther Von Dyck
Walther Franz Anton von Dyck (6 December 1856 – 5 November 1934), born Dyck () and later ennobled, was a German mathematician. He is credited with being the first to define a mathematical group, in the modern sense in . He laid the foundations of combinatorial group theory, being the first to systematically study a group by generators and relations. Biography Von Dyck was a student of Felix Klein, and served as chairman of the commission publishing Klein's encyclopedia. Von Dyck was also the editor of Kepler's works. He promoted technological education as rector of the Technische Hochschule of Munich. He was a Plenary Speaker of the ICM in 1908 at Rome. Von Dyck is the son of the Bavarian painter Hermann Dyck. Legacy The Dyck language in formal language theory is named after him, as are Dyck's theorem and Dyck's surface in the theory of surfaces, together with the von Dyck groups, the Dyck tessellations, Dyck paths, and the Dyck graph In the mathematical field of graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object ''X'' is ''G'' = Sym(''X''). For an object in a metric space, its symmetries form a subgroup of the isometry group of the ambient space. This article mainly considers symmetry groups in Euclidean geometry, but the concept may also be studied for more general types of geometric structure. Introduction We consider the "objects" possessing symmetry to be geometric figures, images, and patterns, such as a wallpaper pattern. For symmetry of physical objects, one may also take their physical composition as part of the pattern. (A pattern may be specified formally as a scalar field, a funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedral Symmetry
In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the icosahedron) and the rhombic triacontahedron. Every polyhedron with icosahedral symmetry has 60 rotational (or orientation-preserving) symmetries and 60 orientation-reversing symmetries (that combine a rotation and a reflection), for a total symmetry order of 120. The full symmetry group is the Coxeter group of type . It may be represented by Coxeter notation and Coxeter diagram . The set of rotational symmetries forms a subgroup that is isomorphic to the alternating group on 5 letters. Description Icosahedral symmetry is a mathematical property of objects indicating that an object has the same symmetries as a regular icosahedron. As point group Apart from the two infinite series of prismatic and antiprismatic symmetry, rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Rowan Hamilton
Sir William Rowan Hamilton Doctor of Law, LL.D, Doctor of Civil Law, DCL, Royal Irish Academy, MRIA, Royal Astronomical Society#Fellow, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, and Royal Astronomer of Ireland, living at Dunsink Observatory. Hamilton's scientific career included the study of geometrical optics, ideas from Fourier analysis, and his work on quaternions which made him one of the founders of modern linear algebra. He made major contributions in optics, classical mechanics and abstract algebra. His work was fundamental to modern theoretical physics, particularly his reformulation of Newtonian mechanics, now called Hamiltonian mechanics. It is now central both to electromagnetism and to quantum mechanics. Early life Hamilton was the fourth of nine children born to Sarah Hutton (1780–1817) and Archibald Hamilton (1778–1819),Bruno (2003) who ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosian Calculus
The icosian calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856. In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations. Hamilton's discovery derived from his attempts to find an algebra of "triplets" or 3-tuples that he believed would reflect the three Cartesian axes. The symbols of the icosian calculus can be equated to moves between vertices on a dodecahedron. Hamilton's work in this area resulted indirectly in the terms Hamiltonian circuit and Hamiltonian path in graph theory. He also invented the icosian game as a means of illustrating and popularising his discovery. Informal definition The algebra is based on three symbols that are each roots of unity, in that repeated application of any of them yields the value 1 after a particular number of steps. They are: : \begin \iota^2 & = 1, \\ \kappa^3 & = 1, \\ \lambda^5 & = 1. \end Hamilton also gives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Burnside Problem
The Burnside problem asks whether a finitely generated group in which every element has finite order must necessarily be a finite group. It was posed by William Burnside in 1902, making it one of the oldest questions in group theory and was influential in the development of combinatorial group theory. It is known to have a negative answer in general, as Evgeny Golod and Igor Shafarevich provided a counter-example in 1964. The problem has many refinements and variants (see bounded and restricted below) that differ in the additional conditions imposed on the orders of the group elements, some of which are still open questions. Brief history Initial work pointed towards the affirmative answer. For example, if a group ''G'' is finitely generated and the order of each element of ''G'' is a divisor of 4, then ''G'' is finite. Moreover, A. I. Kostrikin was able to prove in 1958 that among the finite groups with a given number of generators and a given prime exponent, there exists a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithmically Insoluble
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether arbitrary programs eventually halt when run. Background A decision problem is any arbitrary yes-or-no question on an infinite set of inputs. Because of this, it is traditional to define the decision problem equivalently as the set of inputs for which the problem returns ''yes''. These inputs can be natural numbers, but also other values of some other kind, such as strings of a formal language. Using some encoding, such as a Gödel numbering, the strings can be encoded as natural numbers. Thus, a decision problem informally phrased in terms of a formal language is also equivalent to a set of natural numbers. To keep the formal definition simple, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
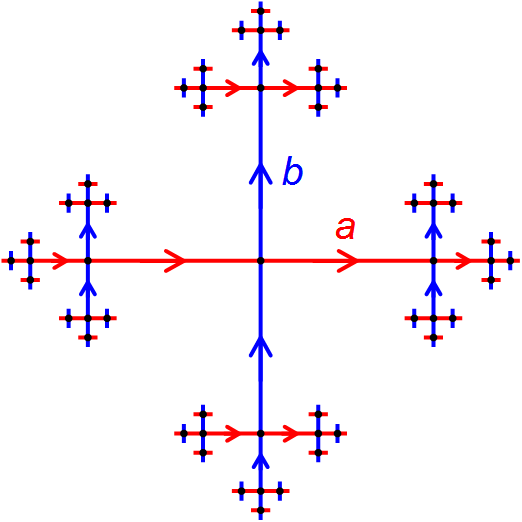
Free Group
In mathematics, the free group ''F''''S'' over a given set ''S'' consists of all words that can be built from members of ''S'', considering two words to be different unless their equality follows from the group axioms (e.g. ''st'' = ''suu''−1''t'', but ''s'' ≠ ''t''−1 for ''s'',''t'',''u'' ∈ ''S''). The members of ''S'' are called generators of ''F''''S'', and the number of generators is the rank of the free group. An arbitrary group ''G'' is called free if it is isomorphic to ''F''''S'' for some subset ''S'' of ''G'', that is, if there is a subset ''S'' of ''G'' such that every element of ''G'' can be written in exactly one way as a product of finitely many elements of ''S'' and their inverses (disregarding trivial variations such as ''st'' = ''suu''−1''t''). A related but different notion is a free abelian group; both notions are particular instances of a free object from universal algebra. As such, free groups are defined by their universal property. History Free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such group (mathematics), groups and topology, topological and geometry, geometric properties of spaces on which these groups Group action (mathematics), act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph (discrete mathematics), graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplicial Complex
In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their ''n''-dimensional counterparts (see illustration). Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex. To distinguish a simplicial from an abstract simplicial complex, the former is often called a geometric simplicial complex.'', Section 4.3'' Definitions A simplicial complex \mathcal is a set of simplices that satisfies the following conditions: :1. Every face of a simplex from \mathcal is also in \mathcal. :2. The non-empty intersection of any two simplices \sigma_1, \sigma_2 \in \mathcal is a face of both \sigma_1 and \sigma_2. See also the definition of an abstract simplicial complex, which loosely speaking is a simplicial complex without an associated geometry. A simplicial ''k''-complex \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |