|
Icosian Calculus
The icosian calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856. In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations. Hamilton's discovery derived from his attempts to find an algebra of "triplets" or 3-tuples that he believed would reflect the three Cartesian axes. The symbols of the icosian calculus can be equated to moves between vertices on a dodecahedron. Hamilton's work in this area resulted indirectly in the terms Hamiltonian circuit and Hamiltonian path in graph theory. He also invented the icosian game as a means of illustrating and popularising his discovery. Informal definition The algebra is based on three symbols that are each roots of unity, in that repeated application of any of them yields the value 1 after a particular number of steps. They are: : \begin \iota^2 & = 1, \\ \kappa^3 & = 1, \\ \lambda^5 & = 1. \end Hamilton also gives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Structure
In mathematics, an algebraic structure consists of a nonempty set ''A'' (called the underlying set, carrier set or domain), a collection of operations on ''A'' (typically binary operations such as addition and multiplication), and a finite set of identities, known as axioms, that these operations must satisfy. An algebraic structure may be based on other algebraic structures with operations and axioms involving several structures. For instance, a vector space involves a second structure called a field, and an operation called ''scalar multiplication'' between elements of the field (called '' scalars''), and elements of the vector space (called '' vectors''). Abstract algebra is the name that is commonly given to the study of algebraic structures. The general theory of algebraic structures has been formalized in universal algebra. Category theory is another formalization that includes also other mathematical structures and functions between structures of the same type (homomor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set and an Binary operation, operation that combines any two Element (mathematics), elements of the set to produce a third element of the set, in such a way that the operation is Associative property, associative, an identity element exists and every element has an Inverse element, inverse. These three axioms hold for Number#Main classification, number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The concept of a group and the axioms that define it were elaborated for handling, in a unified way, essential structural properties of very different mathematical entities such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry groups arise naturally in the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosian
In mathematics, the icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell. The term can be used to refer to two related, but distinct, concepts: * The icosian group: a multiplicative group of 120 quaternions, positioned at the vertices of a 600-cell of unit radius. This group is isomorphic to the binary icosahedral group of order 120. * The icosian ring: all finite sums of the 120 unit icosians. Unit icosians The 120 unit icosians, which form the icosian group, are all even permutations of: * 8 icosians of the form ½(±2, 0, 0, 0) * 16 icosians of the form ½(±1, ±1, ±1, ±1) * 96 icosians of the form ½(0, ±1, ±1''/φ'', ±''φ'') In this case, the vector (''a'', ''b'', ''c'', ''d'') refers to the quaternion ''a'' + ''b''i + ''c''j + ''d''k, and φ represents the golden ratio ( + 1)/2. These 120 vectors form the H4 root syste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History
History (from Greek , ''historia'', meaning "inquiry; knowledge acquired by investigation") is the study and the documentation of the past. Events before the invention of writing systems are considered prehistory. "History" is an umbrella term comprising past events as well as the memory, discovery, collection, organization, presentation, and interpretation of these events. Historians seek knowledge of the past using historical sources such as written documents, oral accounts, art and material artifacts, and ecological markers. History is also an academic discipline which uses narrative to describe, examine, question, and analyze past events, and investigate their patterns of cause and effect. Historians often debate which narrative best explains an event, as well as the significance of different causes and effects. Historians also debate the nature of history as an end in itself, as well as its usefulness to give perspective on the problems of the present. Stories com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Séminaire Lotharingien De Combinatoire
The ''Séminaire Lotharingien de Combinatoire'' (English: ''Lotharingian Seminar of Combinatorics'') is a peer-reviewed academic journal specialising in combinatorial mathematics, named after Lotharingia. It has existed since 1980 as a regular joint seminar in Combinatorics for the Universities of Bayreuth, Erlangen and Strasbourg. In 1994, it was decided to create a journal under the same name. The regular meetings continue to this day. See also *M. Lothaire M. Lothaire is the pseudonym of a group of mathematicians, many of whom were students of Marcel-Paul Schützenberger. The name is used as the author of several of their joint books about combinatorics on words. The group is named for Lothair I.. ... References External links Séminaire Lotharingien de Combinatoire Combinatorics journals Open access journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dessin D'enfant
In mathematics, a dessin d'enfant is a type of graph embedding used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers. The name of these embeddings is French for a "child's drawing"; its plural is either ''dessins d'enfant'', "child's drawings", or ''dessins d'enfants'', "children's drawings". A dessin d'enfant is a graph, with its vertices colored alternately black and white, embedded in an oriented surface that, in many cases, is simply a plane. For the coloring to exist, the graph must be bipartite. The faces of the embedding are required be topological disks. The surface and the embedding may be described combinatorially using a rotation system, a cyclic order of the edges surrounding each vertex of the graph that describes the order in which the edges would be crossed by a path that travels clockwise on the surface in a small loop around the vertex. Any dessin can provide the surface it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
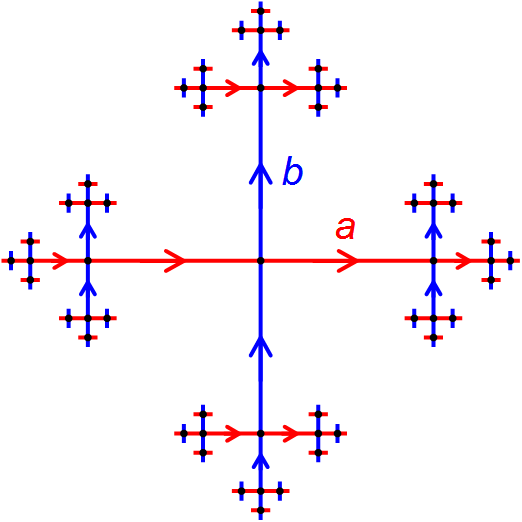
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such group (mathematics), groups and topology, topological and geometry, geometric properties of spaces on which these groups Group action (mathematics), act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph (discrete mathematics), graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Group Theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations. It is much used in geometric topology, the fundamental group of a simplicial complex having in a natural and geometric way such a presentation. A very closely related topic is geometric group theory, which today largely subsumes combinatorial group theory, using techniques from outside combinatorics besides. It also comprises a number of algorithmically insoluble problems, most notably the word problem for groups; and the classical Burnside problem. History See for a detailed history of combinatorial group theory. A proto-form is found in the 1856 icosian calculus of William Rowan Hamilton, where he studied the icosahedral symmetry group via the edge graph of the dodecahedron. The foundations of combinatorial group theory were laid by Walther von Dyck, student of Felix Klein Christian Felix Klein (; 25 April 1849 – 22 Ju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups , and finite Coxeter groups were classified in 1935 . Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras. Standard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Presentation Of A Group
In mathematics, a presentation is one method of specifying a group. A presentation of a group ''G'' comprises a set ''S'' of generators—so that every element of the group can be written as a product of powers of some of these generators—and a set ''R'' of relations among those generators. We then say ''G'' has presentation :\langle S \mid R\rangle. Informally, ''G'' has the above presentation if it is the "freest group" generated by ''S'' subject only to the relations ''R''. Formally, the group ''G'' is said to have the above presentation if it is isomorphic to the quotient of a free group on ''S'' by the normal subgroup generated by the relations ''R''. As a simple example, the cyclic group of order ''n'' has the presentation :\langle a \mid a^n = 1\rangle, where 1 is the group identity. This may be written equivalently as :\langle a \mid a^n\rangle, thanks to the convention that terms that do not include an equals sign are taken to be equal to the group identity. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosian Calculus Iota2
In mathematics, the icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell. The term can be used to refer to two related, but distinct, concepts: * The icosian Group (mathematics), group: a multiplicative group of 120 quaternions, positioned at the vertices of a 600-cell of unit radius. This group is group isomorphism, isomorphic to the binary icosahedral group of order of a group, order 120. * The icosian Ring (mathematics), ring: all finite sums of the 120 unit icosians. Unit icosians The 120 unit icosians, which form the icosian group, are all even permutations of: * 8 icosians of the form ½(±2, 0, 0, 0) * 16 icosians of the form ½(±1, ±1, ±1, ±1) * 96 icosians of the form ½(0, ±1, ±1''/φ'', ±''φ'') In this case, the vector (''a'', ''b'', ''c'', ''d'') refers to the quaternion ''a'' + ''b''i + ''c''j + ''d''k, and φ represents the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |