|
Icosian
In mathematics, the icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell. The term can be used to refer to two related, but distinct, concepts: * The icosian group: a multiplicative group of 120 quaternions, positioned at the vertices of a 600-cell of unit radius. This group is isomorphic to the binary icosahedral group of order 120. * The icosian ring: all finite sums of the 120 unit icosians. Unit icosians The 120 unit icosians, which form the icosian group, are all even permutations of: * 8 icosians of the form ½(±2, 0, 0, 0) * 16 icosians of the form ½(±1, ±1, ±1, ±1) * 96 icosians of the form ½(0, ±1, ±1''/φ'', ±''φ'') In this case, the vector (''a'', ''b'', ''c'', ''d'') refers to the quaternion ''a'' + ''b''i + ''c''j + ''d''k, and φ represents the golden ratio ( + 1)/2. These 120 vectors form the H4 root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral cells. The 600-cell's boundary is composed of 600 tetrahedral cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. It is the 4- dimensional analogue of the icosahedron, since it has five tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex. Its dual polytope is the 120-cell. Geometry The 600-cell is the fifth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity). It can be deconstructed into twenty-five overlapping instances of its immediate predecessor the 24-cell, as the 24-cell can be deconstructed into three overlapping in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
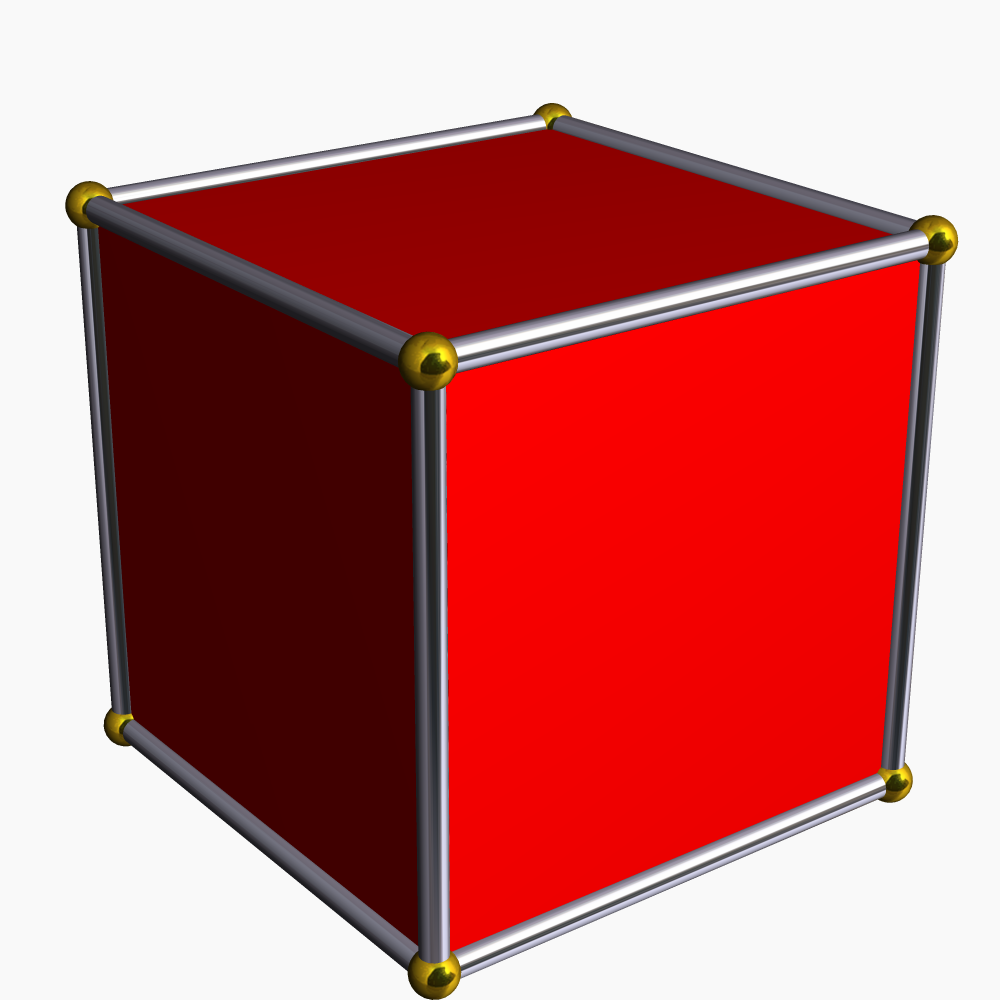
Tesseract
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book '' A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaim Goodman-Strauss
Chaim Goodman-Strauss (born June 22, 1967 in Austin TX) is an American mathematician who works in convex geometry, especially aperiodic tiling. He is on the faculty of the University of Arkansas and is a co-author with John H. Conway of ''The Symmetries of Things'', a comprehensive book surveying the mathematical theory of patterns. Education and career Goodman-Strauss received both his B.S. (1988) and Ph.D. (1994) in mathematics from the University of Texas at Austin.Chaim Goodman-Strauss The College Board His doctoral advisor was John Edwin Luecke. He joined the faculty at the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heidi Burgiel
''Heidi'' (; ) is a work of children's fiction published in 1881 by Swiss author Johanna Spyri, originally published in two parts as ''Heidi: Her Years of Wandering and Learning'' (german: Heidis Lehr- und Wanderjahre) and ''Heidi: How She Used What She Learned'' (german: Heidi kann brauchen, was es gelernt hat). It is a novel about the events in the life of a 5-year-old girl in her paternal grandfather's care in the Swiss Alps. It was written as a book "for children and those who love children" (as quoted from its subtitle). ''Heidi'' is one of the best-selling books ever written and is among the best-known works of Swiss literature. Plot Heidi is an orphaned girl initially raised by her maternal grandmother and aunt Dete in Maienfeld, in the Grisons, after the early deaths of her parents, Tobias and Adelheid (Dete's brother-in-law and sister). Shortly after the grandmother's death, Dete is offered a good job as a maid in the big city, and takes 5-year-old Heidi to her pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neil Sloane
__NOTOC__ Neil James Alexander Sloane (born October 10, 1939) is a British-American mathematician. His major contributions are in the fields of combinatorics, error-correcting codes, and sphere packing. Sloane is best known for being the creator and maintainer of the On-Line Encyclopedia of Integer Sequences (OEIS). Biography Sloane was born in Beaumaris, Anglesey, Wales, in 1939, moving to Cowes, Isle of Wight, England in 1946. The family emigrated to Australia, arriving at the start of 1949. Sloane then moved from Melbourne to the United States in 1961. He studied at Cornell University under Nick DeClaris, Frank Rosenblatt, Frederick Jelinek and Wolfgang Heinrich Johannes Fuchs, receiving his Ph.D. in 1967. His doctoral dissertation was titled ''Lengths of Cycle Times in Random Neural Networks''. Sloane joined AT&T Bell Labs in 1968 and retired from AT&T Labs in 2012. He became an AT&T Fellow in 1998. He is also a Fellow of the Learned Society of Wales, an IEE ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John H
John is a common English name and surname: * John (given name) * John (surname) John may also refer to: New Testament Works * Gospel of John, a title often shortened to John * First Epistle of John, often shortened to 1 John * Second Epistle of John, often shortened to 2 John * Third Epistle of John, often shortened to 3 John People * John the Baptist (died c. AD 30), regarded as a prophet and the forerunner of Jesus Christ * John the Apostle (lived c. AD 30), one of the twelve apostles of Jesus * John the Evangelist, assigned author of the Fourth Gospel, once identified with the Apostle * John of Patmos, also known as John the Divine or John the Revelator, the author of the Book of Revelation, once identified with the Apostle * John the Presbyter, a figure either identified with or distinguished from the Apostle, the Evangelist and John of Patmos Other people with the given name Religious figures * John, father of Andrew the Apostle and Saint Peter * P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups , and finite Coxeter groups were classified in 1935 . Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Form
In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial). For example, :4x^2 + 2xy - 3y^2 is a quadratic form in the variables and . The coefficients usually belong to a fixed field , such as the real or complex numbers, and one speaks of a quadratic form over . If K=\mathbb R, and the quadratic form takes zero only when all variables are simultaneously zero, then it is a definite quadratic form, otherwise it is an isotropic quadratic form. Quadratic forms occupy a central place in various branches of mathematics, including number theory, linear algebra, group theory (orthogonal group), differential geometry ( Riemannian metric, second fundamental form), differential topology ( intersection forms of four-manifolds), and Lie theory (the Killing form). Quadratic forms are not to be confused with a quadratic equation, which has only one variable and includes terms of degree two or less. A quadra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E8 Lattice
In mathematics, the E lattice is a special lattice in R. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8. The name derives from the fact that it is the root lattice of the E root system. The normIn this article, the ''norm'' of a vector refers to its length squared (the square of the ordinary norm). of the E lattice (divided by 2) is a positive definite even unimodular quadratic form in 8 variables, and conversely such a quadratic form can be used to construct a positive-definite, even, unimodular lattice of rank 8. The existence of such a form was first shown by H. J. S. Smith in 1867, and the first explicit construction of this quadratic form was given by Korkin and Zolotarev in 1873. The E lattice is also called the Gosset lattice after Thorold Gosset who was one of the first to study the geometry of the lattice itself around 1900. Lattice points The E lattice is a discrete subgroup of R of full rank (i.e. it spans all of R). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface , or blackboard bold \mathbb. A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real number that is not rational is called irrational. Irrational numbers include , , , and . Since the set of rational numbers is countable, and the set of real numbers is u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells. The boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex figure is a cube. The 24-cell is self-dual. It and the tesseract are the only convex regular 4-polytopes in which the edge length equals the radius. The 24-cell does not have a regular analogue in 3 dimensions. It is the only one of the six convex regular 4-polytopes which is not the four-dimensional analogue of one of the five regular Platonic solids. However, it can be seen as the analogue of a pair of irregular solids: the cuboctahedron and its dual the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |