Calibration (probability)

	Calibration (probability) Calibrated probability assessments are subjective probability, subjective probabilities assigned by individuals who have been trained to assess probabilities in a way that historically represents their uncertainty. For example, when a person has calibrated a situation and says they are "80% confident" in each of 100 predictions they made, they will get about 80% of them correct. Likewise, they will be right 90% of the time they say they are 90% certain, and so on. Calibration training improves subjective probabilities because most people are either "overconfident" or "under-confident" (usually the former). By practicing with a series of trivia questions, it is possible for subjects to fine-tune their ability to assess probabilities. For example, a subject may be asked: :''True or False:'' "A hockey puck fits in a golf hole" :''Confidence:'' Choose the probability that best represents your chance of getting this question right... ::50% 60% 70% 80% 90% 100% If a person has no id ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Subjective Probability Bayesian probability is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectation representing a state of knowledge or as quantification of a personal belief. The Bayesian interpretation of probability can be seen as an extension of propositional logic that enables reasoning with hypotheses; that is, with propositions whose truth or falsity is unknown. In the Bayesian view, a probability is assigned to a hypothesis, whereas under frequentist inference, a hypothesis is typically tested without being assigned a probability. Bayesian probability belongs to the category of evidential probabilities; to evaluate the probability of a hypothesis, the Bayesian probabilist specifies a prior probability. This, in turn, is then updated to a posterior probability in the light of new, relevant data (evidence). The Bayesian interpretation provides a standard set of procedures and formula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Paul J Paul may refer to: Paul (given name), a given name (includes a list of people with that name) Paul (surname), a list of people People Christianity Paul the Apostle (AD c.5–c.64/65), also known as Saul of Tarsus or Saint Paul, early Christian missionary and writer Pope Paul (other), multiple Popes of the Roman Catholic Church Saint Paul (other), multiple other people and locations named "Saint Paul" Roman and Byzantine empire Lucius Aemilius Paullus Macedonicus (c. 229 BC – 160 BC), Roman general Julius Paulus Prudentissimus (), Roman jurist Paulus Catena (died 362), Roman notary Paulus Alexandrinus (4th century), Hellenistic astrologer Paul of Aegina or Paulus Aegineta (625–690), Greek surgeon Royals Paul I of Russia (1754–1801), Tsar of Russia Paul of Greece (1901–1964), King of Greece Other people Paul the Deacon or Paulus Diaconus (c. 720 – c. 799), Italian Benedictine monk Paul (father of Maurice), the father of Maurice, Byzan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Prediction Market Prediction markets (also known as betting markets, information markets, decision markets, idea futures or event derivatives) are open markets where specific outcomes can be predicted using financial incentives. Essentially, they are exchange-traded markets created for the purpose of trading the outcome of events. The market prices can indicate what the crowd thinks the probability of the event is. A prediction market contract trades between 0 and 100%. The most common form of a prediction market is a binary option market, which will expire at the price of 0 or 100%. Prediction markets can be thought of as belonging to the more general concept of crowdsourcing which is specially designed to aggregate information on particular topics of interest. The main purposes of prediction markets are eliciting aggregating beliefs over an unknown future outcome. Traders with different beliefs trade on contracts whose payoffs are related to the unknown future outcome and the market prices of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
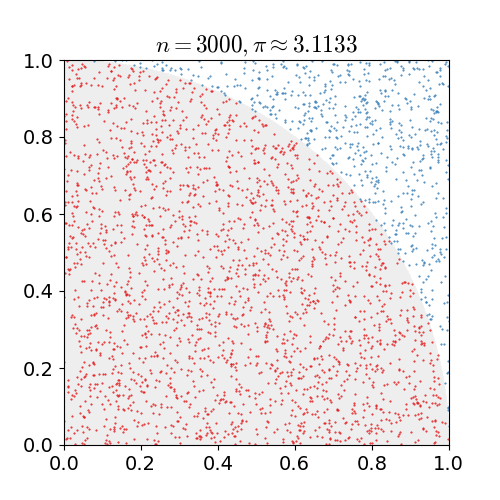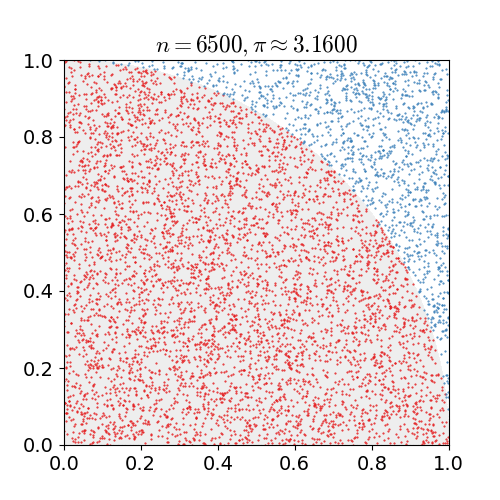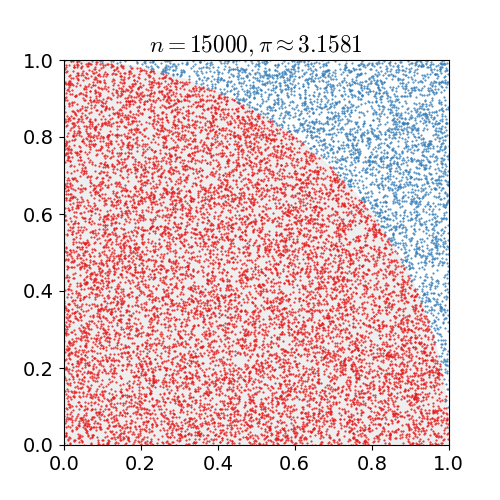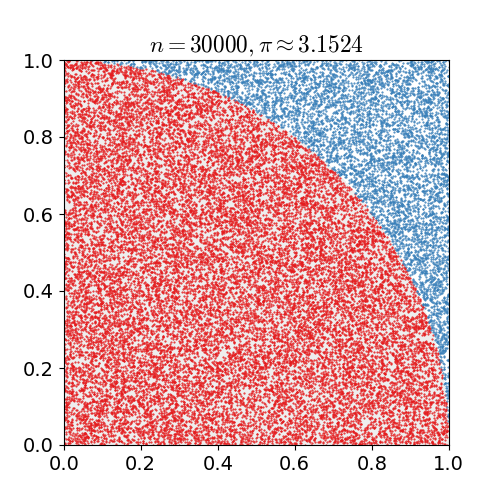
picture info	Monte Carlo Method Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Probability Assessment Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These conce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]