|
Correlation Functions
The cross-correlation matrix of two random vectors is a matrix containing as elements the cross-correlations of all pairs of elements of the random vectors. The cross-correlation matrix is used in various digital signal processing algorithms. Definition For two random vectors \mathbf = (X_1,\ldots,X_m)^ and \mathbf = (Y_1,\ldots,Y_n)^, each containing random elements whose expected value and variance exist, the cross-correlation matrix of \mathbf and \mathbf is defined by and has dimensions m \times n. Written component-wise: :\operatorname_ = \begin \operatorname _1 Y_1& \operatorname _1 Y_2& \cdots & \operatorname _1 Y_n\\ \\ \operatorname _2 Y_1& \operatorname _2 Y_2& \cdots & \operatorname _2 Y_n\\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \operatorname_m Y_1& \operatorname _m Y_2& \cdots & \operatorname _m Y_n\\ \\ \end The random vectors \mathbf and \mathbf need not have the same dimension, and either might be a scalar value. Example For example, if \mathbf = \left ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Vector
In probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose value is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value. The individual variables in a random vector are grouped together because they are all part of a single mathematical system — often they represent different properties of an individual statistical unit. For example, while a given person has a specific age, height and weight, the representation of these features of ''an unspecified person'' from within a group would be a random vector. Normally each element of a random vector is a real number. Random vectors are often used as the underlying implementation of various types of aggregate random variables, e.g. a random matrix, random tree, random sequence, stochastic process, etc. More formally, a multivariate random variable is a column vector \mathbf = (X_1,\dots,X_n)^\mathsf (or its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
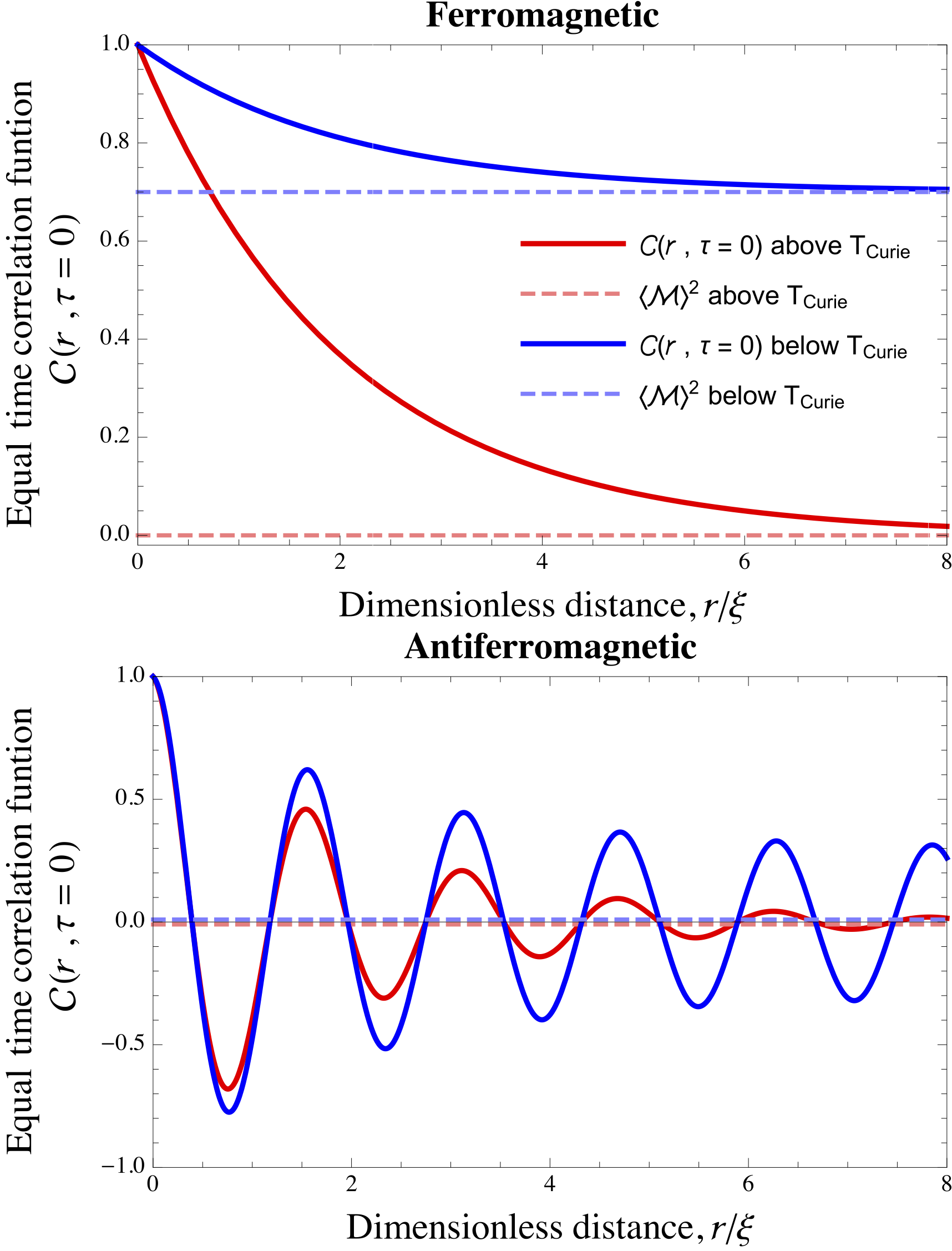
Correlation Function (statistical Mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function. Correlation functions describe how microscopic variables, such as spin and density, at different positions are related. More specifically, correlation functions quantify how microscopic variables co-vary with one another on average across space and time. A classic example of such spatial correlations is in ferro- and antiferromagnetic materials, where the spins prefer to align parallel and antiparallel with their nearest neighbors, respectively. The spatial correlation between spins in such materials is shown in the figure to the right. Definitions The most common definition of a correlation function is the canonical ensemble (thermal) average of the scalar product of two random variables, s_1 and s_2, at positions R and R+r and times t and t+\tau: C (r,\tau) = \langle \mathbf(R,t) \cdot \mathbf(R+r,t+\tau)\rangle\ - \langle \mathbf( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Analysis
Spatial analysis or spatial statistics includes any of the formal techniques which studies entities using their topological, geometric, or geographic properties. Spatial analysis includes a variety of techniques, many still in their early development, using different analytic approaches and applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is the technique applied to structures at the human scale, most notably in the analysis of geographic data or transcriptomics data. Complex issues arise in spatial analysis, many of which are neither clearly defined nor completely resolved, but form the basis for current research. The most fundamental of these is the problem of defining the spatial location of the entities being studied. Classification of the techniques of spatial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forecasting' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance And Correlation
In probability theory and statistics, the mathematical concepts of covariance and correlation are very similar. Both describe the degree to which two random variables or sets of random variables tend to deviate from their expected values in similar ways. If ''X'' and ''Y'' are two random variables, with means (expected values) ''μX'' and ''μY'' and standard deviations ''σX'' and ''σY'', respectively, then their covariance and correlation are as follows: : so that :\rho_ = \sigma_ / (\sigma_X \sigma_Y) where ''E'' is the expected value operator. Notably, correlation is dimensionless while covariance is in units obtained by multiplying the units of the two variables. If ''Y'' always takes on the same values as ''X'', we have the covariance of a variable with itself (i.e. \sigma_), which is called the variance and is more commonly denoted as \sigma_X^2, the square of the standard deviation. The ''correlation'' of a variable with itself is always 1 (except in the dege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Distribution Function
In statistical mechanics, the radial distribution function, (or pair correlation function) g(r) in a system of particles (atoms, molecules, colloids, etc.), describes how density varies as a function of distance from a reference particle. If a given particle is taken to be at the origin O, and if \rho =N/V is the average number density of particles, then the local time-averaged density at a distance r from O is \rho g(r). This simplified definition holds for a homogeneous and isotropic system. A more general case will be considered below. In simplest terms it is a measure of the probability of finding a particle at a distance of r away from a given reference particle, relative to that for an ideal gas. The general algorithm involves determining how many particles are within a distance of r and r+dr away from a particle. This general theme is depicted to the right, where the red particle is our reference particle, and blue particles are those whose centers are within the circul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Distortion Theory
Rate or rates may refer to: Finance * Rates (tax), a type of taxation system in the United Kingdom used to fund local government * Exchange rate, rate at which one currency will be exchanged for another Mathematics and science * Rate (mathematics), a specific kind of ratio, in which two measurements are related to each other (often with respect to time) * Rate function, a function used to quantify the probabilities of a rare event * Reaction rate, in chemistry the speed at which reactants are converted into products Military * Naval rate, a junior enlisted member of a navy * Rating system of the Royal Navy, a former method of indicating a British warship's firepower People * Ed Rate (1899–1990), American football player * José Carlos Rates (1879–1945), General Secretary of the Portuguese Communist Party * Peter of Rates (died 60 AD), traditionally considered to be the first bishop of Braga Other uses * Rate (building), the class of a building in late Georgian and early ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the " amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and Y. MI is the expected value of the pointwise mutual information (PMI). The quantity was defined and analyzed by Claude Shannon in his landmark paper "A Mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Function (quantum Field Theory)
In quantum field theory, correlation functions, often referred to as correlators or Green's functions, are vacuum expectation values of time-ordered products of field operators. They are a key object of study in quantum field theory where they can be used to calculate various observables such as S-matrix elements. Definition For a scalar field theory with a single field \phi(x) and a vacuum state , \Omega\rangle at every event (x) in spacetime, the n-point correlation function is the vacuum expectation value of the time-ordered products of n field operators in the Heisenberg picture G_n(x_1,\dots, x_n) = \langle \Omega, T\, \Omega\rangle. Here T\ is the time-ordering operator for which orders the field operators so that earlier time field operators appear to the right of later time field operators. By transforming the fields and states into the interaction picture, this is rewritten as G_n(x_1, \dots, x_n) = \frac, where , 0\rangle is the ground state of the free theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Function (astronomy)
In astronomy, a correlation function describes the distribution of galaxies in the universe. By default, "correlation function" refers to the two-point autocorrelation function. The two-point autocorrelation function is a function of one variable (distance); it describes the excess probability of finding two galaxies separated by this distance (excess over and above the probability that would arise if the galaxies were simply scattered independently and with uniform probability). It can be thought of as a clumpiness factor - the higher the value for some distance scale, the more clumpy the universe is at that distance scale. The following definition (from Peebles 1980) is often cited: : ''Given a random galaxy in a location, the correlation function describes the probability that another galaxy will be found within a given distance.'' However, it can only be correct in the statistical sense that it is averaged over a large number of galaxies chosen as the first, ''random'' ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Element
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line. The concept was introduced by who commented that the “development of probability theory and expansion of area of its applications have led to necessity to pass from schemes where (random) outcomes of experiments can be described by number or a finite set of numbers, to schemes where outcomes of experiments represent, for example, vectors, functions, processes, fields, series, transformations, and also sets or collections of sets.” The modern-day usage of “random element” frequently assumes the space of values is a topological vector space, often a Banach or Hilbert space with a specified natural sigma algebra of subsets. Definition Let (\Omega, \mathcal, P) be a probability space, and (E, \mathcal) a measurable space. A random element with values in ''E'' is a function which is (\mathcal, \mathcal)-measurable. That is, a fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's ''r'', the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |