|
Correlation Function (astronomy)
In astronomy, a correlation function describes the distribution of objects (often stars or galaxies) in the universe. By default, "correlation function" refers to the two-point autocorrelation function. The two-point autocorrelation function is a function of one variable (distance); it describes the excess probability of finding two galaxies separated by this distance (excess over and above the probability that would arise if the galaxies were simply scattered independently and with uniform probability). It can be thought of as a "clumpiness" factor - the higher the value for some distance scale, the more "clumpy" the universe is at that distance scale. The following definition (from Peebles 1980) is often cited: : ''Given a random galaxy in a location, the correlation function describes the probability that another galaxy will be found within a given distance.'' However, it can only be correct in the statistical sense that it is averaged over a large number of galaxies cho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest include planets, natural satellite, moons, stars, nebulae, galaxy, galaxies, meteoroids, asteroids, and comets. Relevant phenomena include supernova explosions, gamma ray bursts, quasars, blazars, pulsars, and cosmic microwave background radiation. More generally, astronomy studies everything that originates beyond atmosphere of Earth, Earth's atmosphere. Cosmology is a branch of astronomy that studies the universe as a whole. Astronomy is one of the oldest natural sciences. The early civilizations in recorded history made methodical observations of the night sky. These include the Egyptian astronomy, Egyptians, Babylonian astronomy, Babylonians, Greek astronomy, Greeks, Indian astronomy, Indians, Chinese astronomy, Chinese, Maya civilization, M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Space
In mathematics, physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency (and possibly phase), rather than time, as in time series. While a time-domain graph shows how a signal changes over time, a frequency-domain graph shows how the signal is distributed within different frequency bands over a range of frequencies. A complex valued frequency-domain representation consists of both the magnitude and the phase of a set of sinusoids (or other basis waveforms) at the frequency components of the signal. Although it is common to refer to the magnitude portion (the real valued frequency-domain) as the frequency response of a signal, the phase portion is required to uniquely define the signal. A given function or signal can be converted between the time and frequency domains with a pair of mathematical operators called transforms. An example is the Fourier transform, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Process
In statistics and probability theory, a point process or point field is a set of a random number of mathematical points randomly located on a mathematical space such as the real line or Euclidean space. Kallenberg, O. (1986). ''Random Measures'', 4th edition. Academic Press, New York, London; Akademie-Verlag, Berlin. , .Daley, D.J, Vere-Jones, D. (1988). ''An Introduction to the Theory of Point Processes''. Springer, New York. , . Point processes on the real line form an important special case that is particularly amenable to study,Last, G., Brandt, A. (1995).''Marked point processes on the real line: The dynamic approach.'' Probability and its Applications. Springer, New York. , because the points are ordered in a natural way, and the whole point process can be described completely by the (random) intervals between the points. These point processes are frequently used as models for random events in time, such as the arrival of customers in a queue (queueing theory), of impulses i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Function
A correlation function is a function that gives the statistical correlation between random variables, contingent on the spatial or temporal distance between those variables. If one considers the correlation function between random variables representing the same quantity measured at two different points, then this is often referred to as an autocorrelation function, which is made up of autocorrelations. Correlation functions of different random variables are sometimes called cross-correlation functions to emphasize that different variables are being considered and because they are made up of cross-correlations. Correlation functions are a useful indicator of dependencies as a function of distance in time or space, and they can be used to assess the distance required between sample points for the values to be effectively uncorrelated. In addition, they can form the basis of rules for interpolating values at points for which there are no observations. Correlation functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Descriptive Statistics
Spatial descriptive statistics is the intersection of spatial statistics and descriptive statistics; these methods are used for a variety of purposes in geography, particularly in quantitative data analyses involving Geographic Information Systems (GIS). Types of spatial data The simplest forms of spatial data are ''gridded data'', in which a scalar quantity is measured for each point in a regular grid of points, and ''point sets'', in which a set of coordinates (e.g. of points in the plane) is observed. An example of gridded data would be a satellite image of forest density that has been digitized on a grid. An example of a point set would be the latitude/longitude coordinates of all elm trees in a particular plot of land. More complicated forms of data include marked point sets and spatial time series. Measures of spatial central tendency The coordinate-wise mean of a point set is the centroid, which solves the same variational problem in the plane (or higher-dimensional E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Cosmology
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of fundamental questions about its Cosmogony, origin, structure, Chronology of the universe, evolution, and ultimate fate.For an overview, see Cosmology as a science originated with the Copernican principle, which implies that astronomical object, celestial bodies obey identical physical laws to those on Earth, and Newtonian mechanics, which first allowed those physical laws to be understood. Physical cosmology, as it is now understood, began in 1915 with the development of Albert Einstein's general relativity, general theory of relativity, followed by major observational discoveries in the 1920s: first, Edwin Hubble discovered that the universe contains a huge number of external Galaxy, galaxies beyond the Milky Way; then, work by Vesto Sliph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
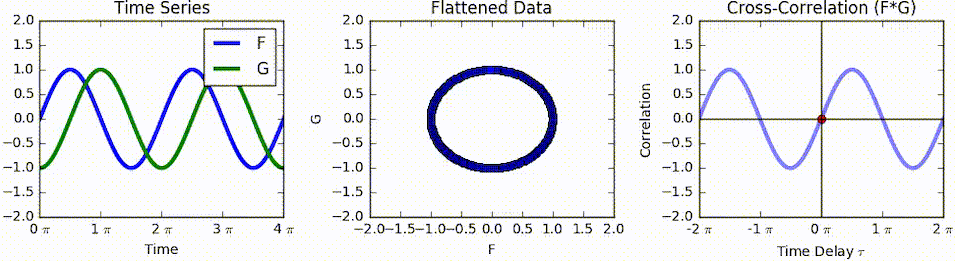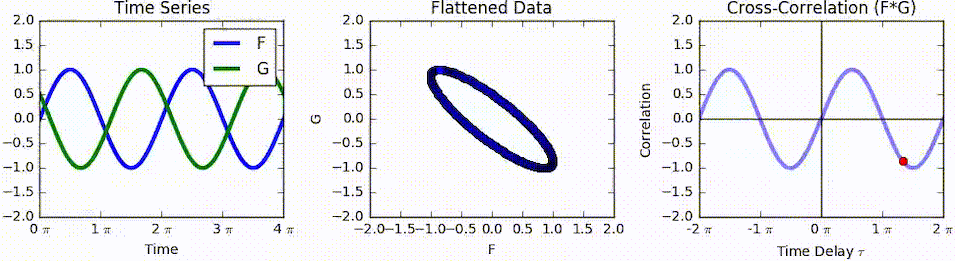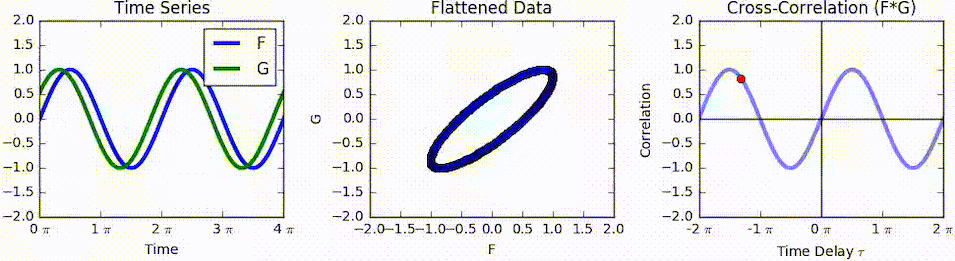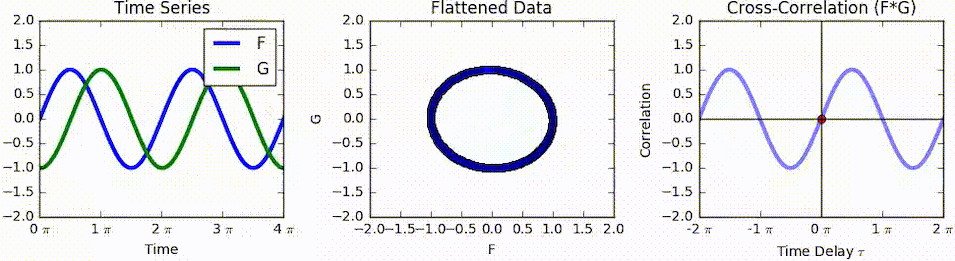
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy. In probability and statistics, the term ''cross-correlations'' refers to the correlations between the entries of two random vectors \mathbf and \mathbf, while the ''correlations'' of a random vector \mathbf are the correlations between the entries of \mathbf itself, those forming the correlation mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Spectrum
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of Power (physics), power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including Noise (electronics), noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar (physics)
Scalar quantities or simply scalars are physical quantities that can be described by a single pure number (a ''scalar'', typically a real number), accompanied by a unit of measurement, as in "10cm" (ten centimeters). Examples of scalar are length, mass, charge, volume, and time. Scalars may represent the magnitude of physical quantities, such as speed is to velocity. Scalars do not represent a direction. Scalars are unaffected by changes to a vector space basis (i.e., a coordinate rotation) but may be affected by translations (as in relative speed). A change of a vector space basis changes the description of a vector in terms of the basis used but does not change the vector itself, while a scalar has nothing to do with this change. In classical physics, like Newtonian mechanics, rotations and reflections preserve scalars, while in relativity, Lorentz transformations or space-time translations preserve scalars. The term "scalar" has origin in the multiplication o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star
A star is a luminous spheroid of plasma (physics), plasma held together by Self-gravitation, self-gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night sky, night; their immense distances from Earth make them appear as fixed stars, fixed points of light. The most prominent stars have been categorised into constellations and asterism (astronomy), asterisms, and many of the brightest stars have proper names. Astronomers have assembled star catalogues that identify the known stars and provide standardized stellar designations. The observable universe contains an estimated to stars. Only about 4,000 of these stars are visible to the naked eye—all within the Milky Way galaxy. A star's life star formation, begins with the gravitational collapse of a gaseous nebula of material largely comprising hydrogen, helium, and traces of heavier elements. Its stellar mass, total mass mainly determines it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |