|
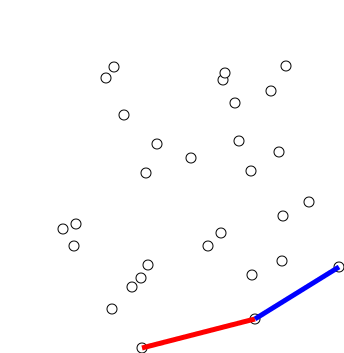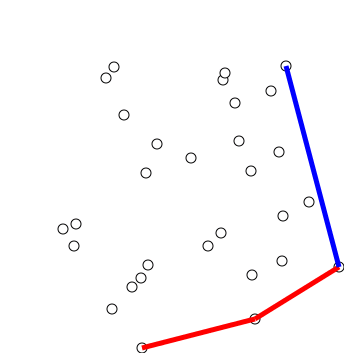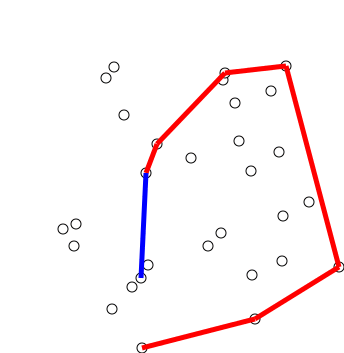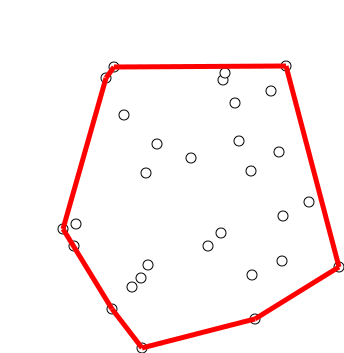
Convex Hull Of A Simple Polygon
In discrete geometry and computational geometry, the convex hull of a simple polygon is the polygon of minimum perimeter that contains a given simple polygon. It is a special case of the more general concept of a convex hull. It can be computed in linear time, faster than algorithms for convex hulls of point sets. The convex hull of a simple polygon can be subdivided into the given polygon itself and into polygonal ''pockets'' bounded by a polygonal chain of the polygon together with a single convex hull edge. Repeatedly reflecting an arbitrarily chosen pocket across this convex hull edge produces a sequence of larger simple polygons; according to the Erdős–Nagy theorem, this process eventually terminates with a convex polygon. Structure The convex hull of a simple polygon is itself a convex polygon. Overlaying the original simple polygon onto its convex hull partitions this convex polygon into regions, one of which is the original polygon. The remaining regions are called ''p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graham Scan
Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(''n'' log ''n''). It is named after Ronald Graham, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently. Algorithm The first step in this algorithm is to find the point with the lowest y-coordinate. If the lowest y-coordinate exists in more than one point in the set, the point with the lowest x-coordinate out of the candidates should be chosen. Call this point ''P''. This step takes O(''n''), where ''n'' is the number of points in question. Next, the set of points must be sorted in increasing order of the angle they and the point ''P'' make with the x-axis. Any general-purpose sorting algorithm is appropriate for this, for example heapsort (which is O(''n'' log ''n'')). Sorting in order of angle does not require ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ACM Transactions On Graphics
''ACM Transactions on Graphics'' (TOG) is a bimonthly peer-reviewed scientific journal that covers the field of computer graphics. It was established in 1982 and is published by the Association for Computing Machinery. TOG publishes two special issues for ACM SIGGRAPH's conference proceedings. Starting in 2003, all papers accepted for presentation at the annual SIGGRAPH conference are printed in a special summer issue of the journal. Beginning in 2008, papers presented at SIGGRAPH Asia are printed in a special November/December issue. The editor-in-chief is Carol O'Sullivan (Trinity College Dublin). According to the ''Journal Citation Reports'', the journal had a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 5.414. The journal ranks 1st in computer graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Algorithms
Elsevier () is a Dutch academic publishing company specializing in scientific, technical, and medical content. Its products include journals such as ''The Lancet'', '' Cell'', the ScienceDirect collection of electronic journals, '' Trends'', the '' Current Opinion'' series, the online citation database Scopus, the SciVal tool for measuring research performance, the ClinicalKey search engine for clinicians, and the ClinicalPath evidence-based cancer care service. Elsevier's products and services also include digital tools for data management, instruction, research analytics and assessment. Elsevier is part of the RELX Group (known until 2015 as Reed Elsevier), a publicly traded company. According to RELX reports, in 2021 Elsevier published more than 600,000 articles annually in over 2,700 journals; as of 2018 its archives contained over 17 million documents and 40,000 e-books, with over one billion annual downloads. Researchers have criticized Elsevier for its high profit margi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Processing Letters
''Information Processing Letters'' is a peer reviewed scientific journal in the field of computer science, published by Elsevier. The aim of the journal is to enable fast dissemination of results in the field of information processing Information processing is the change (processing) of information in any manner detectable by an observer. As such, it is a process that ''describes'' everything that happens (changes) in the universe, from the falling of a rock (a change in posi ... in the form of short papers. Submissions are limited to nine double-spaced pages. Both theoretical and experimental research is covered. External links * Computer science journals Publications established in 1971 Semi-monthly journals Elsevier academic journals {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deque
In computer science, a double-ended queue (abbreviated to deque, pronounced ''deck'', like "cheque") is an abstract data type that generalizes a queue, for which elements can be added to or removed from either the front (head) or back (tail). It is also often called a head-tail linked list, though properly this refers to a specific data structure ''implementation'' of a deque (see below). Naming conventions ''Deque'' is sometimes written ''dequeue'', but this use is generally deprecated in technical literature or technical writing because ''dequeue'' is also a verb meaning "to remove from a queue". Nevertheless, several libraries and some writers, such as Aho, Hopcroft, and Ullman in their textbook ''Data Structures and Algorithms'', spell it ''dequeue''. John Mitchell, author of ''Concepts in Programming Languages,'' also uses this terminology. Distinctions and sub-types This differs from the queue abstract data type or ''first in first out'' list ( FIFO), where elements ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piecewise Smooth
In mathematics, a piecewise-defined function (also called a piecewise function, a hybrid function, or definition by cases) is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. Piecewise definition is actually a way of expressing the function, rather than a characteristic of the function itself. A distinct, but related notion is that of a property holding piecewise for a function, used when the domain can be divided into intervals on which the property holds. Unlike for the notion above, this is actually a property of the function itself. A piecewise linear function (which happens to be also continuous) is depicted as an example. Notation and interpretation Piecewise functions can be defined using the common functional notation, where the body of the function is an array of functions and associated subdomains. These subdomains together must cover the whole domain; often it is also required that they are pai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stack (abstract Data Type)
In computer science, a stack is an abstract data type that serves as a collection of elements, with two main operations: * Push, which adds an element to the collection, and * Pop, which removes the most recently added element that was not yet removed. Additionally, a peek operation can, without modifying the stack, return the value of the last element added. Calling this structure a ''stack'' is by analogy to a set of physical items stacked one atop another, such as a stack of plates. The order in which an element added to or removed from a stack is described as last in, first out, referred to by the acronym LIFO. As with a stack of physical objects, this structure makes it easy to take an item off the top of the stack, but accessing a datum deeper in the stack may require taking off multiple other items first. Considered as a linear data structure, or more abstractly a sequential collection, the push and pop operations occur only at one end of the structure, referred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polygon
In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a simple polygon (not self-intersecting). Equivalently, a polygon is convex if every line that does not contain any edge intersects the polygon in at most two points. A strictly convex polygon is a convex polygon such that no line contains two of its edges. In a convex polygon, all interior angles are less than or equal to 180 degrees, while in a strictly convex polygon all interior angles are strictly less than 180 degrees. Properties The following properties of a simple polygon are all equivalent to convexity: *Every internal angle is strictly less than 180 degrees. *Every point on every line segment between two points inside or on the boundary of the polygon remains inside or on the boundary. *The polygon is entirely contained in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object. Discrete geometry has a large overlap with convex geometry and computational geometry, and is closely related to subjects such as finite geometry, combinatorial optimization, digital geometry, discrete differential geometry, geometric graph theory, toric geometry, and combinatorial topology. History Although polyhedra and tessellations had been studied for many years by people such as Kepler and Cauchy, modern discrete geometry has its origins in the late 19th century. Early ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erdős–Nagy Theorem
The Erdős–Nagy theorem is a result in discrete geometry stating that a non-convex simple polygon can be made into a convex polygon by a finite sequence of flips. The flips are defined by taking a convex hull of a polygon and reflecting a pocket with respect to the boundary edge. The theorem is named after mathematicians Paul Erdős and Béla Szőkefalvi-Nagy. Statement A ''pocket'' of a non-convex simple polygon is a simple polygon bounded by a consecutive sequence of edges of the polygon together with a single edge of its convex hull that is not an edge of the polygon itself. Every convex hull edge that is not a polygon edge defines a pocket in this way. A ''flip'' of a pocket is obtained by reflecting the polygon edges that bound the pocket, across a reflection line containing the convex hull edge. Because the reflected pocket lies entirely within the reflected image of the convex hull, on the other side of this line, this operation cannot introduce any crossings, so t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygonal Chain
In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points (A_1, A_2, \dots, A_n) called its vertices. The curve itself consists of the line segments connecting the consecutive vertices. Name A polygonal chain may also be called a polygonal curve, polygonal path, polyline,. piecewise linear curve, broken line or, in geographic information systems, a linestring or linear ring. Variations A simple polygonal chain is one in which only consecutive (or the first and the last) segments intersect and only at their endpoints. A closed polygonal chain is one in which the first vertex coincides with the last one, or, alternatively, the first and the last vertices are also connected by a line segment. A simple closed polygonal chain in the plane is the boundary of a simple polygon. Often the term "polygon" is used in the meaning of "closed polygonal chain", but in some cases it is important to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |