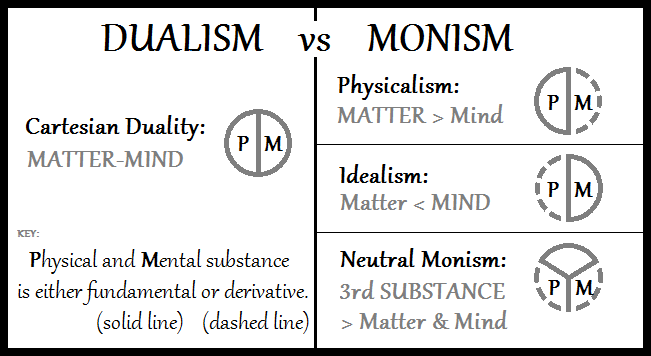
|
Computational Metaphysics
Abstract object theory (AOT) is a branch of metaphysics regarding abstract objects. Originally devised by metaphysician Edward Zalta in 1981, the theory was an expansion of mathematical Platonism. Overview ''Abstract Objects: An Introduction to Axiomatic Metaphysics'' (1983) is the title of a publication by Edward Zalta that outlines abstract object theory. AOT is a dual predication approach (also known as "dual copula strategy") to abstract objectsDale Jacquette, ''Meinongian Logic: The Semantics of Existence and Nonexistence'', Walter de Gruyter, 1996, p. 17. influenced by the contributions of Alexius MeinongZalta (1983:xi). and his student Ernst Mally. On Zalta's account, there are two modes of predication: some objects (the ordinary concrete ones around us, like tables and chairs) ''exemplify'' properties, while others (abstract objects like numbers, and what others would call "non-existent objects", like the round square, and the mountain made entirely of gold) merely ''en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metaphysics
Metaphysics is the branch of philosophy that studies the fundamental nature of reality, the first principles of being, identity and change, space and time, causality, necessity, and possibility. It includes questions about the nature of consciousness and the relationship between mind and matter, between substance and attribute, and between potentiality and actuality. The word "metaphysics" comes from two Greek words that, together, literally mean "after or behind or among he study ofthe natural". It has been suggested that the term might have been coined by a first century CE editor who assembled various small selections of Aristotle's works into the treatise we now know by the name ''Metaphysics'' (μετὰ τὰ φυσικά, ''meta ta physika'', 'after the ''Physics'' ', another of Aristotle's works). Metaphysics studies questions related to what it is for something to exist and what types of existence there are. Metaphysics seeks to answer, in an abstract and fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guise Theory
Guise (; nl, Wieze) is a commune in the Aisne department in Hauts-de-France in northern France. The city was the birthplace of the noble family of Guise, Dukes of Guise, who later became Princes of Joinville. Population Sights The remains of the medieval castle of Guise, the seat of the Dukes of Guise, is within the commune. Economy Guise is the agricultural centre of the northern area of Aisne. Miscellaneous Guise was the birthplace of Camille Desmoulins (1760–1794), a journalist and politician who played an important part in the French Revolution, and that of Jeanne Macherez who was a heroine during the World War I. Over a period of 20 years, beginning about 1856, Jean-Baptiste Godin built the (the Social Palace), an industrial and communal residential complex that was a separate community within Guise. It expressed many of his ideas about developing social sympathy through improved housing and services for workers and their families, influenced by the ideas of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Object Of The Mind
An object of the mind is an object that exists in the imagination, but which, in the real world, can only be represented or modeled. Some such objects are abstractions, literary concepts, or fictional scenarios. Closely related are intentional objects, which are what thoughts and feelings are about, even if they are not about anything real (such as thoughts about unicorns, or feelings of apprehension about a dental appointment which is subsequently cancelled). However, intentional objects may coincide with real objects (as in thoughts about horses, or a feeling of regret about a missed appointment). Mathematical objects Mathematics and geometry describe abstract objects that sometimes correspond to familiar shapes, and sometimes do not. Circles, triangles, rectangles, and so forth describe two-dimensional shapes that are often found in the real world. However, mathematical formulas do not describe individual physical circles, triangles, or rectangles. They describe ideal shapes th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Neo-logicism
In the philosophy of mathematics, logicism is a programme comprising one or more of the theses that — for some coherent meaning of 'logic' — mathematics is an extension of logic, some or all of mathematics is reducible to logic, or some or all of mathematics may be modelled in logic. Bertrand Russell and Alfred North Whitehead Alfred North Whitehead (15 February 1861 – 30 December 1947) was an English mathematician and philosopher. He is best known as the defining figure of the philosophical school known as process philosophy, which today has found applicat ... championed this programme, initiated by Gottlob Frege and subsequently developed by Richard Dedekind and Giuseppe Peano. Overview Dedekind's path to logicism had a turning point when he was able to construct a model satisfying the Axiom, axioms characterizing the real numbers using certain sets of Rational number, rational numbers. This and related ideas convinced him that arithmetic, algebra and analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Meinongianism
Noneism, also known as modal Meinongianism (named after Alexius Meinong), is a theory in logic and metaphysics. It holds that some things do not exist. It was first coined by Richard Routley in 1980 and appropriated again in 2005 by Graham Priest. Overview Noneism holds that some things do not exist. That is, we can quantify over non-existent objects ("items") using the so-called particular quantifier (also known—misleadingly in the view of noneists—as the existential quantifier). They also hold that "there is" is like "exist", rather than like the particular quantifier. Thus, they deny that ''there are'' things that do not exist. On this theory, there are no empty names, wherefore the "problem of empty names" that afflicts many theories about names (in particular, Millianism), is not a problem at all. While Priest also espouses dialetheism, he maintains that his dialetheism is mostly capable of being separated out from his noneism. The connection is that impossible objects m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Universe Hypothesis
In physics and cosmology, the mathematical universe hypothesis (MUH), also known as the ultimate ensemble theory and struogony (from mathematical structure, Latin: struō), is a speculative "theory of everything" (TOE) proposed by cosmologist Max Tegmark. Description Tegmark's MUH is: ''Our external physical reality is a mathematical structure''. That is, the physical universe is not merely ''described by'' mathematics, but ''is'' mathematics (specifically, a mathematical structure). Mathematical existence equals physical existence, and all structures that exist mathematically exist physically as well. Observers, including humans, are "self-aware substructures (SASs)". In any mathematical structure complex enough to contain such substructures, they "will subjectively perceive themselves as existing in a physically 'real' world". The theory can be considered a form of Pythagoreanism or Platonism in that it proposes the existence of mathematical entities; a form of mathematicism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Of Concepts
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathematics. He wrote works on philosophy, theology, ethics, politics, law, history and philology. Leibniz also made major contributions to physics and technology, and anticipated notions that surfaced much later in probability theory, biology, medicine, geology, psychology, linguistics and computer science. In addition, he contributed to the field of library science: while serving as overseer of the Wolfenbüttel library in Germany, he devised a cataloging system that would have served as a guide for many of Europe's largest libraries. Leibniz's contributions to this vast array of subjects were scattered in various learned journals, in tens of thousands of letters and in unpublished manuscripts. He wrote in several languages, primarily in Lat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstractionism (philosophy Of Mathematics)
Structuralism is a theory in the philosophy of mathematics that holds that mathematical theories describe structures of mathematical objects. Mathematical objects are exhaustively defined by their place in such structures. Consequently, structuralism maintains that mathematical objects do not possess any intrinsic properties but are defined by their external relations in a system. For instance, structuralism holds that the number 1 is exhaustively defined by being the successor of 0 in the structure of the theory of natural numbers. By generalization of this example, any natural number is defined by its respective place in that theory. Other examples of mathematical objects might include lines and planes in geometry, or elements and operations in abstract algebra. Structuralism is an epistemologically realistic view in that it holds that mathematical statements have an objective truth value. However, its central claim only relates to what ''kind'' of entity a mathematical obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edward N
Edward is an English given name. It is derived from the Anglo-Saxon name ''Ēadweard'', composed of the elements '' ēad'' "wealth, fortune; prosperous" and '' weard'' "guardian, protector”. History The name Edward was very popular in Anglo-Saxon England, but the rule of the Norman and Plantagenet dynasties had effectively ended its use amongst the upper classes. The popularity of the name was revived when Henry III named his firstborn son, the future Edward I, as part of his efforts to promote a cult around Edward the Confessor, for whom Henry had a deep admiration. Variant forms The name has been adopted in the Iberian peninsula since the 15th century, due to Edward, King of Portugal, whose mother was English. The Spanish/Portuguese forms of the name are Eduardo and Duarte. Other variant forms include French Édouard, Italian Edoardo and Odoardo, German, Dutch, Czech and Romanian Eduard and Scandinavian Edvard. Short forms include Ed, Eddy, Eddie, Ted, Teddy and Ned ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automated Reasoning
In computer science, in particular in knowledge representation and reasoning and metalogic, the area of automated reasoning is dedicated to understanding different aspects of reasoning. The study of automated reasoning helps produce computer programs that allow computers to reason completely, or nearly completely, automatically. Although automated reasoning is considered a sub-field of artificial intelligence, it also has connections with theoretical computer science and philosophy. The most developed subareas of automated reasoning are automated theorem proving (and the less automated but more pragmatic subfield of interactive theorem proving) and automated proof checking (viewed as guaranteed correct reasoning under fixed assumptions). Extensive work has also been done in reasoning by analogy using induction and abduction. Other important topics include reasoning under uncertainty and non-monotonic reasoning. An important part of the uncertainty field is that of argumentation, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branden Fitelson
Branden Fitelson (; born August 17, 1969) is an American philosopher and Distinguished Professor of Philosophy at Northeastern University. He is known for his expertise on formal epistemology and philosophy of science. Bibliography * Edward N. Zalta and Branden Fitelson"Steps Toward a Computational Metaphysics" ''Journal of Philosophical Logic'' 36(2) (April 2007): 227–247. See also *Evolutionary argument against naturalism *Minimal axioms for Boolean algebra In mathematical logic, minimal axioms for Boolean algebra are assumptions which are equivalent to the axioms of Boolean algebra (or propositional calculus), chosen to be as short as possible. For example, if one chooses to take commutativity for gra ... References External links *Branden Fitelson at Northeastern University [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Schema
In mathematical logic, an axiom schema (plural: axiom schemata or axiom schemas) generalizes the notion of axiom. Formal definition An axiom schema is a formula in the metalanguage of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which may or may not be required to satisfy certain conditions. Often, such conditions require that certain variables be free, or that certain variables not appear in the subformula or term. Finite axiomatization Given that the number of possible subformulas or terms that can be inserted in place of a schematic variable is countably infinite, an axiom schema stands for a countably infinite set of axioms. This set can usually be defined recursively. A theory that can be axiomatized without schemata is said to be finitely axiomatized. Theories that can be finitely axiomatized are seen as a bit more metamathematically elegant, even if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
