|
Compressible (Littlestone And Warmuth)
In thermodynamics and fluid mechanics, the compressibility (also known as the coefficient of compressibility or, if the temperature is held constant, the isothermal compressibility) is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure (or mean stress) change. In its simple form, the compressibility \kappa (denoted in some fields) may be expressed as :\beta =-\frac\frac, where is volume and is pressure. The choice to define compressibility as the negative of the fraction makes compressibility positive in the (usual) case that an increase in pressure induces a reduction in volume. The reciprocal of compressibility at fixed temperature is called the isothermal bulk modulus. Definition The specification above is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is isentropic or isothermal. Accordingly, isothermal compressibility is defined: :\beta_T=-\frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Properties (thermodynamics)
The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are: * Compressibility (or its inverse, the bulk modulus) :* Isothermal compressibility ::\kappa_T=-\frac\left(\frac\right)_T \quad = -\frac\,\frac :* Adiabatic compressibility ::\kappa_S=-\frac\left(\frac\right)_S \quad = -\frac\,\frac * Specific heat (Note - the extensive analog is the heat capacity) :* Specific heat at constant pressure ::c_P=\frac\left(\frac\right)_P \quad = -\frac\,\frac :* Specific heat at constant volume ::c_V=\frac\left(\frac\right)_V \quad = -\frac\,\frac * Coefficient of thermal expansion ::\alpha=\frac\left(\frac\right)_P \quad = \frac\,\frac where ''P'' is pressure, ''V'' is volume, ''T'' is temperature, ''S'' is entropy, and ''N'' is the number of particles. For a single comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressibility Equation
In statistical mechanics and thermodynamics the compressibility equation refers to an equation which relates the isothermal compressibility (and indirectly the pressure) to the structure of the liquid. It reads:kT\left(\frac\right)=1+\rho \int_V \mathrm \mathbf (r)-1where \rho is the number density, g(r) is the radial distribution function and kT\left(\frac\right) is the isothermal compressibility. Using the Fourier representation of the Ornstein-Zernike equation the compressibility equation can be rewritten in the form: \frac\left(\frac\right) = \frac=\frac=1-\rho\hat(0)=1-\rho \int c(r) \mathrm \mathbf where h(r) and c(r) are the indirect and direct correlation functions respectively. The compressibility equation is one of the many integral equations in statistical mechanics In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature. Temperature is important in all fields of natur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressibility Factor
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour.Properties of Natural Gases . Includes a chart of compressibility factors versus reduced pressure and reduced temperature (on last page of the PDF document) In general, deviation from ideal behaviour becomes more significant the closer a gas is to a |
Ideal Gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions. Under various conditions of temperature and pressure, many real gases behave qualitatively like an ideal gas where the gas molecules (or atoms for monatomic gas) play the role of the ideal particles. Many gases such as nitrogen, oxygen, hydrogen, noble gases, some heavier gases like carbon dioxide and mixtures such as air, can be treated as ideal gases within reasonable tolerances over a considerable parameter range around standard temperature and pressure. Generally, a gas behaves more like an ideal gas at higher temperature and lower pressu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Gas
Real gases are nonideal gases whose molecules occupy space and have interactions; consequently, they do not adhere to the ideal gas law. To understand the behaviour of real gases, the following must be taken into account: *compressibility effects; *variable specific heat capacity; *van der Waals forces; *non-equilibrium thermodynamic effects; *issues with molecular dissociation and elementary reactions with variable composition For most applications, such a detailed analysis is unnecessary, and the ideal gas approximation can be used with reasonable accuracy. On the other hand, real-gas models have to be used near the condensation point of gases, near critical points, at very high pressures, to explain the Joule–Thomson effect, and in other less usual cases. The deviation from ideality can be described by the compressibility factor Z. Models Van der Waals model Real gases are often modeled by taking into account their molar weight and molar volume :RT = \left(p + \frac\ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Properties
In thermodynamics, a physical property is any property that is measurable, and whose value describes a state of a physical system. Thermodynamic properties are defined as characteristic features of a system, capable of specifying the system's state. Some constants, such as the ideal gas constant, , do not describe the state of a system, and so are not properties. On the other hand, some constants, such as (the freezing point depression constant, or cryoscopic constant), depend on the identity of a substance, and so may be considered to describe the state of a system, and therefore may be considered physical properties. "Specific" properties are expressed on a per mass basis. If the units were changed from per mass to, for example, per mole, the property would remain as it was (i.e., intensive or extensive). Regarding work and heat Work and heat are not thermodynamic properties, but rather '' process quantities:'' flows of energy across a system boundary. Systems do not ''co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
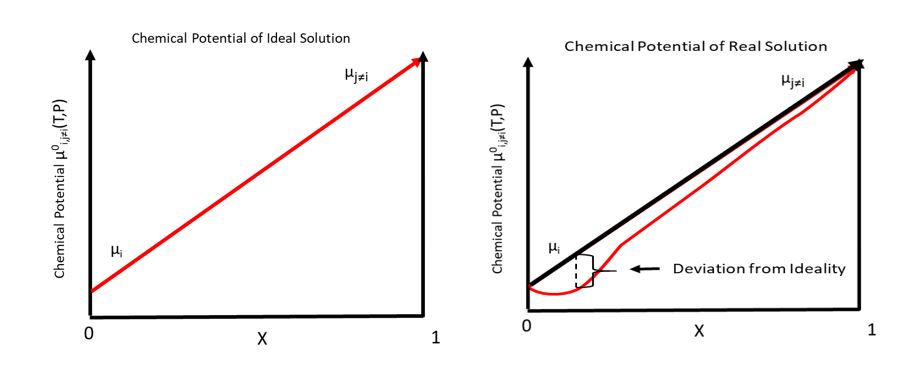
Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Pressure Coefficient
In thermodynamics, thermal pressure (also known as the thermal pressure coefficient) is a measure of the relative pressure change of a fluid or a solid as a response to a temperature change at constant volume. The concept is related to the Pressure-Temperature Law, also known as Amontons's law or Gay-Lussac's law. In general pressure, (P) can be written as the following sum: P_\text(V,T) = P_\text(V,T) + \Delta P_\text(V,T). P_\text is the pressure required to compress the material from its volume V_0 to volume V at a constant temperature T_0. The second term expresses the change in thermal pressure \Delta P_ . This is the pressure change at constant volume due to the temperature difference between T_0 and T. Thus, it is the pressure change along an Isochoric process, isochore of the material. The thermal pressure \gamma_v is customarily expressed in its simple form as \gamma_v =\left( \frac \right)_. Thermodynamic definition Because of the equivalences between many properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient Of Thermal Expansion
Thermal expansion is the tendency of matter to change its shape A shape or figure is a graphics, graphical representation of an object or its external boundary, outline, or external Surface (mathematics), surface, as opposed to other properties such as color, Surface texture, texture, or material type. A pl ..., area, volume, and density in response to a change in temperature, usually not including phase transitions. Temperature is a monotonic function of the average molecular kinetic energy of a substance. When a substance is heated, molecules begin to vibrate and move more, usually creating more distance between themselves. Substances which contract with increasing temperature are unusual, and only occur within limited temperature ranges (see examples below). The relative expansion (also called strain (mechanics), strain) divided by the change in temperature is called the material's coefficient of linear thermal expansion and generally varies with temperature. As energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the ''isentropic expansion factor'' and is denoted by ( gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
