|
Closed Geodesic
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold is a geodesic that returns to its starting point with the same tangent direction. It may be formalized as the projection of a closed orbit of the geodesic, geodesic flow on the tangent space of the manifold. Definition In a Riemannian manifold (''M'',''g''), a closed geodesic is a curve \gamma:\mathbb R\rightarrow M that is a geodesic for the metric ''g'' and is periodic. Closed geodesics can be characterized by means of a variational principle. Denoting by \Lambda M the space of smooth 1-periodic curves on ''M'', closed geodesics of period 1 are precisely the critical point (mathematics), critical points of the energy function E:\Lambda M\rightarrow\mathbb R, defined by : E(\gamma)=\int_0^1 g_(\dot\gamma(t),\dot\gamma(t))\,\mathrmt. If \gamma is a closed geodesic of period ''p'', the reparametrized curve t\mapsto\gamma(pt) is a closed geodesic of period 1, and therefore it is a critical poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fuchsian Group
In mathematics, a Fuchsian group is a discrete subgroup of PSL(2,R). The group PSL(2,R) can be regarded equivalently as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting on any of these spaces. There are some variations of the definition: sometimes the Fuchsian group is assumed to be finitely generated, sometimes it is allowed to be a subgroup of PGL(2,R) (so that it contains orientation-reversing elements), and sometimes it is allowed to be a Kleinian group (a discrete subgroup of PSL(2,C)) which is conjugate to a subgroup of PSL(2,R). Fuchsian groups are used to create Fuchsian models of Riemann surfaces. In this case, the group may be called the Fuchsian group of the surface. In some sense, Fuchsian groups do for non-Euclidean geometry what crystallographic groups do for Euclidean geometry. Some Escher graphics are based on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Besse
Arthur Besse is a pseudonym chosen by a group of French differential geometers, led by Marcel Berger, following the model of Nicolas Bourbaki. A number of monographs have appeared under the name. Bibliography * ** *Actes de la Table Ronde de Géométrie Différentielle. roceedings of the Roundtable on Differential GeometryEn l'honneur de Marcel Berger. n honor of Marcel BergerHeld in Luminy, July 12–18, 1992. Edited by Arthur L. Besse. Séminaires et Congrès eminars and Congresses 1. Société Mathématique de France, Paris; distributed by American Mathematical Society, Providence, RI, 1996. *Besse, Arthur L.: Some trends in Riemannian geometry. Duration and change, 71–105, Springer, Berlin, 1994 . *Besse, A. Многообразия Эйнштейна. Том I,II. (Russian) instein manifolds. Vol. I, IITranslated from the English and with a preface by D. V. Alekseevskiĭ. "Mir", Moscow, 1990. Vol. I: 320 pp.; Vol. II: pp. 321–704. *Besse, Arthur L.: E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zoll Surface
In mathematics, particularly in differential geometry, a Zoll surface, named after Otto Zoll, is a surface homeomorphic to the 2-sphere, equipped with a Riemannian metric all of whose geodesics are closed and of equal length. While the usual unit-sphere metric on ''S''2 obviously has this property, it also has an infinite-dimensional family of geometrically distinct deformations that are still Zoll surfaces. In particular, most Zoll surfaces do not have constant curvature. Zoll, a student of David Hilbert, discovered the first non-trivial examples. See also * Funk transform In the mathematical field of integral geometry, the Funk transform (also known as Minkowski–Funk transform, Funk–Radon transform or spherical Radon transform) is an integral transform defined by integrating a function on great circles of the s ...: The original motivation for studying the Funk transform was to describe Zoll metrics on the sphere. References * * * * * External links Tannery's pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Selberg Zeta Function
The Selberg zeta-function was introduced by . It is analogous to the famous Riemann zeta function : \zeta(s) = \prod_ \frac where \mathbb is the set of prime numbers. The Selberg zeta-function uses the lengths of simple closed geodesics instead of the primes numbers. If \Gamma is a subgroup of SL(2,R), the associated Selberg zeta function is defined as follows, :\zeta_\Gamma(s)=\prod_p(1-N(p)^)^, or :Z_\Gamma(s)=\prod_p\prod^\infty_(1-N(p)^), where ''p'' runs over conjugacy classes of prime geodesics (equivalently, conjugacy classes of primitive hyperbolic elements of \Gamma), and ''N''(''p'') denotes the length of ''p'' (equivalently, the square of the bigger eigenvalue of ''p''). For any hyperbolic surface of finite area there is an associated Selberg zeta-function; this function is a meromorphic function defined in the complex plane. The zeta function is defined in terms of the closed geodesics of the surface. The zeros and poles of the Selberg zeta-function, ''Z''(''s' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Selberg Trace Formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of a Lie group on the space of square-integrable functions, where is a cofinite discrete group. The character is given by the trace of certain functions on . The simplest case is when is cocompact, when the representation breaks up into discrete summands. Here the trace formula is an extension of the Frobenius formula for the character of an induced representation of finite groups. When is the cocompact subgroup of the real numbers , the Selberg trace formula is essentially the Poisson summation formula. The case when is not compact is harder, because there is a continuous spectrum, described using Eisenstein series. Selberg worked out the non-compact case when is the group ; the extension to higher rank groups is the Arthur–Selberg trace formula. When is the fundamental group of a Riemann surface, the Selberg trace formula describes the spectru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
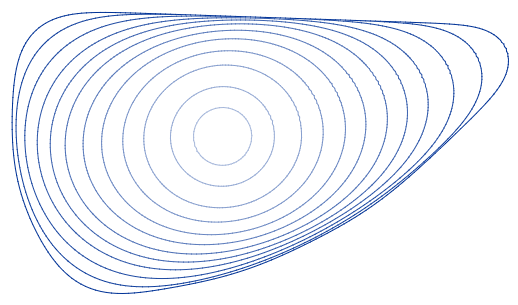
Curve-shortening Flow
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution. As the points of any smooth simple closed curve move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its total absolute curvature decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a single point of singularity. If two disjoint simple smooth closed curves evolve, they remain disjo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorem Of The Three Geodesics
In differential geometry the theorem of the three geodesics, also known as Lyusternik–Schnirelmann theorem, states that every Riemannian manifold with the topology of a sphere has at least three simple closed geodesics (i.e. three embedded geodesic circles). The result can also be extended to quasigeodesics on a convex polyhedron, and to closed geodesics of reversible Finsler 2-spheres. The theorem is sharp: although every Riemannian 2-sphere contains infinitely many distinct closed geodesics, only three of them are guaranteed to have no self-intersections. For example, by a result of Morse if the lengths of three principal axes of an ellipsoid are distinct, but sufficiently close to each other, then the ellipsoid has only three simple closed geodesics. History and proof A geodesic, on a Riemannian surface, is a curve that is locally straight at each of its points. For instance, on the Euclidean plane the geodesics are lines, and on the surface of a sphere the geodesics are gre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lyusternik–Fet Theorem
In mathematics, the Lyusternik–Fet theorem states that on every compact Riemannian manifold there exists a closed geodesic. It is named after Lazar Lyusternik and Abram Ilyich Fet Abram Fet (russian: Абрам Ильич Фет) (5 December 1924 — 30 July 2009) was a Russian mathematician, Soviet dissident, philosopher, Samizdat translator and writer. He used various pseudonyms for Samizdat, like N. A. Klenov, A.B. N .... References * https://www.encyclopediaofmath.org/index.php/Closed_geodesic * L.A. Lyusternik, A.I. Fet, "Variational problems on closed manifolds" Dokl. Akad. Nauk. SSSR, 81 (1951) pp. 17–18 (In Russian) Differential geometry Geodesic (mathematics) {{DEFAULTSORT:Lyusternik-Fet theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugacy Class
In mathematics, especially group theory, two elements a and b of a group are conjugate if there is an element g in the group such that b = gag^. This is an equivalence relation whose equivalence classes are called conjugacy classes. In other words, each conjugacy class is closed under b = gag^. for all elements g in the group. Members of the same conjugacy class cannot be distinguished by using only the group structure, and therefore share many properties. The study of conjugacy classes of non-abelian groups is fundamental for the study of their structure. For an abelian group, each conjugacy class is a set containing one element (singleton set). Functions that are constant for members of the same conjugacy class are called class functions. Definition Let G be a group. Two elements a, b \in G are conjugate if there exists an element g \in G such that gag^ = b, in which case b is called of a and a is called a conjugate of b. In the case of the general linear group \operatorna ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
