|
Center Of Momentum
In physics, the center-of-momentum frame (also zero-momentum frame or COM frame) of a system is the unique (up to velocity but not origin) inertial frame in which the total momentum of the system vanishes. The ''center of momentum'' of a system is not a location (but a collection of relative momenta/velocities: a reference frame). Thus "center of momentum" means "center-of-momentum frame" and is a short form of this phrase.Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, A special case of the center-of-momentum frame is the center-of-mass frame: an inertial frame in which the center of mass (which is a physical point) remains at the origin. In all COM frames, the center of mass is at rest, but it is not necessarily at the origin of the coordinate system. In special relativity, the COM frame is necessarily unique only when the system is isolated. Properties General The center of momentum frame is defined as the inertial frame in which the sum of the linear momen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Massless Particle
In particle physics, a massless particle is an elementary particle whose invariant mass is zero. There are two known gauge boson massless particles: the photon (carrier of electromagnetism) and the gluon (carrier of the strong force). However, gluons are never observed as free particles, since they are confined within hadrons. In addition the Weyl semimetal or Weyl fermion discovered in 2015 is also massless. Neutrinos were originally thought to be massless. However, because neutrinos change flavor as they travel, at least two of the types of neutrinos must have mass. The discovery of this phenomenon, known as neutrino oscillation, led to Canadian scientist Arthur B. McDonald and Japanese scientist Takaaki Kajita sharing the 2015 Nobel prize in physics. *Note that although literal Weyl fermions have never been experimentally confirmed to physically exist, certain systems can act collectively such that they seem to contain Weyl fermion quasiparticles. See also *Relativistic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Centers
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometrie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frames Of Reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathematically (with numerical coordinate values) and physically (signaled by conventional markers). For ''n'' dimensions, reference points are sufficient to fully define a reference frame. Using rectangular Cartesian coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the ''n'' coordinate axes. In Einsteinian relativity, reference frames are used to specify the relationship between a moving observer and the phenomenon under observation. In this context, the term often becomes observational frame of reference (or observational reference frame), which implies that the observer is at rest in the frame, although not necessarily located at its origin. A relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Systems
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the ''number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate of a po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical mechanics, if the present state is known, it is possible to predict how it will move in the future (determinism), and how it has moved in the past (reversibility). The earliest development of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on foundational works of Sir Isaac Newton, and the mathematical methods invented by Gottfried Wilhelm Leibniz, Joseph-Louis Lagrange, Leonhard Euler, and other contemporaries, in the 17th century to describe the motion of bodies under the influence of a system of forces. Later, more abstract methods were developed, leading to the reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances, ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Breit Frame
In particle physics, the Breit frame (also known as infinite-momentum frame or IMF) is a frame of reference used to describe scattering experiments of the form A + B \rightarrow A + \sum C_i, that is experiments in which particle A scatters off particle B, possibly producing particles C_i in the process. The frame is defined so that the particle A has its momentum reversed in the scattering process. Another way of understanding the Breit frame is to look at the elastic scattering A+\gamma \rightarrow A'. The Breit frame is defined as the frame in which \vec_A+\vec_=0. There are different occasions when Breit frame can be useful, e.g., in measuring the electromagnetic form factor of a hadron, A is the scattered hadron; while for deep inelastic scattering process, the elastically scattered parton should be considered as A. It is only in the latter case the Breit frame gets related to infinite-momentum frame. It is named after the American physicist Gregory Breit. See also *Center- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laboratory Frame Of Reference
In theoretical physics, a local reference frame (local frame) refers to a coordinate system or frame of reference that is only expected to function over a small region or a restricted region of space or spacetime. The term is most often used in the context of the application of local inertial frames to small regions of a gravitational field. Although gravitational tidal forces will cause the background geometry to become noticeably non-Euclidean over larger regions, if we restrict ourselves to a sufficiently small region containing a cluster of objects falling together in an ''effectively'' uniform gravitational field, their physics can be described as the physics of that cluster in a space free from explicit background gravitational effects. Equivalence principle When constructing his general theory of relativity, Einstein made the following observation: a freely falling object in a gravitational field will not be able to detect the existence of the field by making local meas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Mass
In physics, the reduced mass is the "effective" Mass#Inertial mass, inertial mass appearing in the two-body problem of Newtonian mechanics. It is a quantity which allows the two-body problem to be solved as if it were a one-body problem. Note, however, that the mass determining the gravitational force is ''not'' reduced. In the computation, one mass ''can'' be replaced with the reduced mass, if this is compensated by replacing the other mass with the sum of both masses. The reduced mass is frequently denoted by \mu (Mu (letter), mu), although the standard gravitational parameter is also denoted by \mu (as are Mu (letter)#Physics and engineering, a number of other physical quantities). It has the dimensional analysis, dimensions of mass, and SI unit kg. Equation Given two bodies, one with mass ''m''1 and the other with mass ''m''2, the equivalent one-body problem, with the position of one body with respect to the other as the unknown, is that of a single body of mass :\mu = \c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
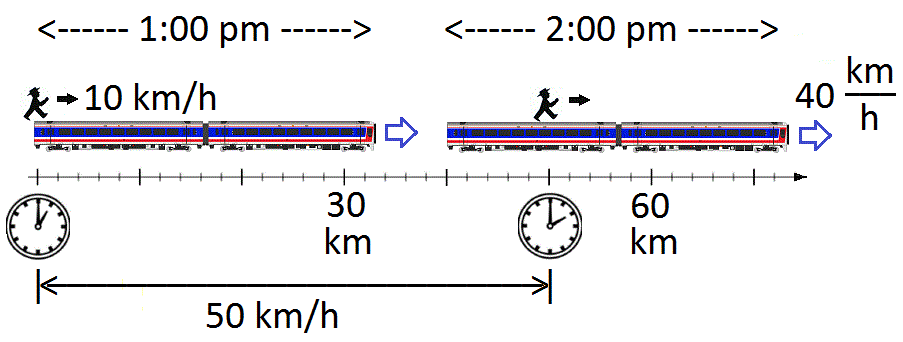
Relative Velocity
The relative velocity \vec_ (also \vec_ or \vec_) is the velocity of an object or observer B in the rest frame of another object or observer A. Classical mechanics In one dimension (non-relativistic) We begin with relative motion in the classical, (or non- relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and by train) for one hour. This, by definition, is 50 km/h, which suggests that the prescription for calculating relative velocity in thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics, qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galilean Transformations
In physics, a Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. These transformations together with spatial rotations and translations in space and time form the inhomogeneous Galilean group (assumed throughout below). Without the translations in space and time the group is the homogeneous Galilean group. The Galilean group is the group of motions of Galilean relativity acting on the four dimensions of space and time, forming the Galilean geometry. This is the passive transformation point of view. In special relativity the homogenous and inhomogenous Galilean transformations are, respectively, replaced by the Lorentz transformations and Poincaré transformations; conversely, the group contraction in the classical limit of Poincaré transformations yields Galilean transformations. The equations below are only physically valid in a Newtonian framework, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |