|
Relative Velocity
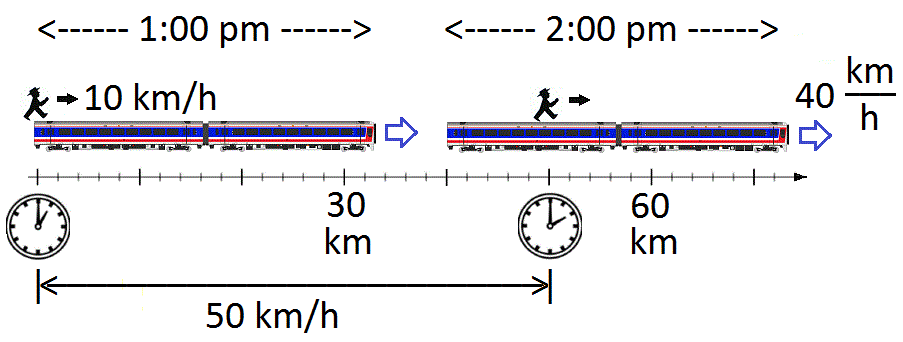
The relative velocity \vec_ (also \vec_ or \vec_) is the velocity of an object or observer B in the rest frame of another object or observer A. Classical mechanics In one dimension (non-relativistic) We begin with relative motion in the classical, (or non- relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and by train) for one hour. This, by definition, is 50 km/h, which suggests that the prescription for calculating relative velocity in thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Motion Man On Train
Relative may refer to: General use *Kinship and family, the principle binding the most basic social units society. If two people are connected by circumstances of birth, they are said to be ''relatives'' Philosophy *Relativism, the concept that points of view have no absolute truth or validity, having only relative, subjective value according to differences in perception and consideration, or relatively, as in the relative value of an object to a person *Relative value (philosophy) Economics *Relative value (economics) Popular culture Film and television * ''Relatively Speaking'' (1965 play), 1965 British play * ''Relatively Speaking'' (game show), late 1980s television game show * ''Everything's Relative'' (episode)#Yu-Gi-Oh! (Yu-Gi-Oh! Duel Monsters), 2000 Japanese anime ''Yu-Gi-Oh! Duel Monsters'' episode *'' Relative Values'', 2000 film based on the play of the same name. *''It's All Relative'', 2003-4 comedy television series *''Intelligence is Relative'', tag line for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed
In everyday use and in kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero. Speed is not the same as velocity. Speed has the dimensions of distance divided by time. The SI unit of speed is the metre per second (m/s), but the most common unit of speed in everyday usage is the kilometre per hour (km/h) or, in the US and the UK, miles per hour (mph). For air and marine travel, the knot is commonly used. The fastest possible speed at which energy or information can travel, according to special relativity, is the speed of light in a vacuum ''c'' = metres per second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Quantities
A physical quantity is a physical property of a material or system that can be quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ' Numerical value ' and a ' Unit '. For example, the physical quantity of mass can be quantified as '32.3 kg ', where '32.3' is the numerical value and 'kg' is the Unit. A physical quantity possesses at least two characteristics in common. # Numerical magnitude. # Units Symbols and nomenclature International recommendations for the use of symbols for quantities are set out in ISO/IEC 80000, the IUPAP red book and the Quantities, Units and Symbols in Physical Chemistry, IUPAC green book. For example, the recommended symbol for the physical quantity ''mass'' is ''m'', and the recommended symbol for the quantity ''electric charge'' is ''Q''. Subscripts and indices Subscripts are used for two reasons, to simply attach a name to the quantity or associate it with another quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Velocity (astronomy)
In astronomy, stellar kinematics is the observational study or measurement of the kinematics or motions of stars through space. Stellar kinematics encompasses the measurement of stellar velocities in the Milky Way and its satellites as well as the internal kinematics of more distant galaxies. Measurement of the kinematics of stars in different subcomponents of the Milky Way including the thin disk, the thick disk, the bulge, and the stellar halo provides important information about the formation and evolutionary history of our Galaxy. Kinematic measurements can also identify exotic phenomena such as hypervelocity stars escaping from the Milky Way, which are interpreted as the result of gravitational encounters of binary stars with the supermassive black hole at the Galactic Center. Stellar kinematics is related to but distinct from the subject of stellar dynamics, which involves the theoretical study or modeling of the motions of stars under the influence of gravity. Stellar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relativistic Speed
Relativistic speed refers to speed at which relativistic effects become significant to the desired accuracy of measurement of the phenomenon being observed. Relativistic effects are those discrepancies between values calculated by models considering and not considering relativity. Related words are velocity, rapidity, and celerity which is proper velocity. Speed is a scalar, being the magnitude of the velocity vector which in relativity is the four-velocity and in three-dimension Euclidean space a three-velocity. Speed is empirically measured as average speed, although current devices in common use can estimate speed over very small intervals and closely approximate instantaneous speed. Non-relativistic discrepancies include cosine error which occurs in speed detection devices when only one scalar component of the three-velocity is measured and the Doppler effect which may affect observations of wavelength and frequency. Relativistic effects are highly non-linear and for everyda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rapidity
In relativity, rapidity is commonly used as a measure for relativistic velocity. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with distance and time coordinates. For one-dimensional motion, rapidities are additive whereas velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite. Using the inverse hyperbolic function , the rapidity corresponding to velocity is where ''c'' is the velocity of light. For low speeds, is approximately . Since in relativity any velocity is constrained to the interval the ratio satisfies . The inverse hyperbolic tangent has the unit interval for its domain and the whole real line for its image; that is, the interval maps onto . History In 1908 Hermann Minkowski expl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Velocity
The radial velocity or line-of-sight velocity, also known as radial speed or range rate, of a target with respect to an observer is the temporal rate of change, rate of change of the distance or Slant range, range between the two points. It is equivalent to the vector projection of the target-observer relative velocity onto the relative direction (geometry), relative direction connecting the two points. In astronomy, the point is usually taken to be the observer on Earth, so the radial velocity then denotes the speed with which the object moves away from the Earth (or approaches it, for a negative radial velocity). Formulation Given a differentiable vector \mathbf \in \mathbb^3 defining the instantaneous position of a target relative to an observer. Let with \mathbf \in \mathbb^3, the instantaneous velocity of the target with respect to the observer. The magnitude of the position vector \mathbf is defined as The quantity range rate is the time derivative of the magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Range Rate
The radial velocity or line-of-sight velocity, also known as radial speed or range rate, of a target with respect to an observer is the temporal rate of change, rate of change of the distance or Slant range, range between the two points. It is equivalent to the vector projection of the target-observer relative velocity onto the relative direction (geometry), relative direction connecting the two points. In astronomy, the point is usually taken to be the observer on Earth, so the radial velocity then denotes the speed with which the object moves away from the Earth (or approaches it, for a negative radial velocity). Formulation Given a differentiable vector \mathbf \in \mathbb^3 defining the instantaneous position of a target relative to an observer. Let with \mathbf \in \mathbb^3, the instantaneous velocity of the target with respect to the observer. The magnitude of the position vector \mathbf is defined as The quantity range rate is the time derivative of the magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Motion
Proper motion is the astrometric measure of the observed changes in the apparent places of stars or other celestial objects in the sky, as seen from the center of mass of the Solar System, compared to the abstract background of the more distant stars. The components for proper motion in the equatorial coordinate system (of a given epoch, often J2000.0) are given in the direction of right ascension (''μ''α) and of declination (''μ''δ). Their combined value is computed as the ''total proper motion'' (''μ''). It has dimensions of angle per time, typically arcseconds per year or milliarcseconds per year. Knowledge of the proper motion, distance, and radial velocity allows calculations of an object's motion from our star system's frame of reference and its motion from the galactic frame of reference – that is motion in respect to the Sun, and by coordinate transformation, that in respect to the Milky Way. Introduction Over the course of centuries, stars appear t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peculiar Velocity
Peculiar motion or peculiar velocity refers to the velocity of an object relative to a ''rest frame'' — usually a frame in which the average velocity of some objects is zero. Galactic astronomy In galactic astronomy, peculiar motion refers to the motion of an object (usually a star) relative to a Galactic rest frame. Local objects are commonly examined as to their vectors of position angle and radial velocity. These can be combined through vector addition to state the object's motion relative to the Sun. Velocities for local objects are sometimes reported with respect to the local standard of rest (LSR) – the average local motion of material in the galaxy – instead of the Sun's rest frame. Translating between the LSR and heliocentric rest frames requires the calculation of the Sun's peculiar velocity in the LSR. Cosmology In physical cosmology, peculiar velocity refers to the components of a galaxy's velocity that deviate from the Hubble flow. According to Hu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Doppler Effect
The Doppler effect or Doppler shift (or simply Doppler, when in context) is the change in frequency of a wave in relation to an observer who is moving relative to the wave source. It is named after the Austrian physicist Christian Doppler, who described the phenomenon in 1842. A common example of Doppler shift is the change of pitch heard when a vehicle sounding a horn approaches and recedes from an observer. Compared to the emitted frequency, the received frequency is higher during the approach, identical at the instant of passing by, and lower during the recession. The reason for the Doppler effect is that when the source of the waves is moving towards the observer, each successive wave crest is emitted from a position closer to the observer than the crest of the previous wave. Therefore, each wave takes slightly less time to reach the observer than the previous wave. Hence, the time between the arrivals of successive wave crests at the observer is reduced, causing an increa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Transformation
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz. The most common form of the transformation, parametrized by the real constant v, representing a velocity confined to the -direction, is expressed as \begin t' &= \gamma \left( t - \frac \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end where and are the coordinates of an event in two frames with the origins coinciding at 0, where the primed frame is seen from the unprimed frame as moving with speed along the -axis, where is the speed of light, and \gamma = \left ( \sqrt\right )^ is the Lorentz factor. When speed is much smaller than , the Lorentz factor is negligibly different from 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |