|
Bicubic Interpolation
In mathematics, bicubic interpolation is an extension of cubic spline interpolation (a method of applying cubic interpolation to a data set) for interpolating data points on a two-dimensional regular grid. The interpolated surface (meaning the kernel shape, not the image) is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation. Bicubic interpolation can be accomplished using either Lagrange polynomials, cubic splines, or cubic convolution algorithm. In image processing, bicubic interpolation is often chosen over bilinear or nearest-neighbor interpolation in image resampling, when speed is not an issue. In contrast to bilinear interpolation, which only takes 4 pixels (2×2) into account, bicubic interpolation considers 16 pixels (4×4). Images resampled with bicubic interpolation can have different interpolation artifacts, depending on the b and c values chosen. Computation Suppose the function values f and the deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bilinear Interpolation
In mathematics, bilinear interpolation is a method for interpolating functions of two variables (e.g., ''x'' and ''y'') using repeated linear interpolation. It is usually applied to functions sampled on a 2D rectilinear grid, though it can be generalized to functions defined on the vertices of (a mesh of) arbitrary convex quadrilaterals. Bilinear interpolation is performed using linear interpolation first in one direction, and then again in another direction. Although each step is linear in the sampled values and in the position, the interpolation as a whole is not linear but rather quadratic in the sample location. Bilinear interpolation is one of the basic resampling techniques in computer vision and image processing, where it is also called bilinear filtering or bilinear texture mapping. Computation Suppose that we want to find the value of the unknown function ''f'' at the point (''x'', ''y''). It is assumed that we know the value of ''f'' at the four points ''Q''11 = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bézier Surface
Bézier surfaces are a type of mathematical spline used in computer graphics, computer-aided design, and finite element modeling. As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive and, for many applications, mathematically convenient. History Bézier surfaces were first described in 1962 by the French engineer Pierre Bézier who used them to design automobile bodies. Bézier surfaces can be of any degree, but bicubic Bézier surfaces generally provide enough degrees of freedom for most applications. Equation A given Bézier surface of degree (''n'', ''m'') is defined by a set of (''n'' + 1)(''m'' + 1) control points k''i'',''j'' where ''i'' = 0, ..., ''n'' and ''j'' = 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acutance
In photography, acutance describes a subjective perception of visual acuity that is related to the edge contrast of an image. Acutance is related to the magnitude of the gradient of brightness. Due to the nature of the human visual system, an image with higher acutance appears sharper even though an increase in acutance does not increase real resolution. Historically, acutance was enhanced chemically during development of a negative (high acutance developers), or by optical means in printing ( unsharp masking). In digital photography, onboard camera software and image postprocessing tools such as Photoshop or GIMP offer various sharpening facilities, the most widely used of which is known as "unsharp mask" because the algorithm is derived from the eponymous analog processing method. In the example image, two light gray lines were drawn on a gray background. As the transition is instantaneous, the line is as sharp as can be represented at this resolution. Acutance in the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
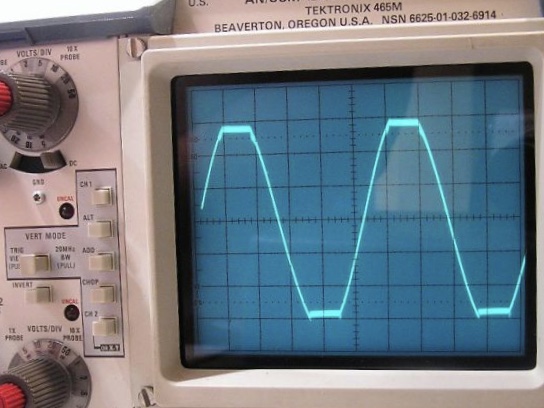
Ringing Artifacts
In signal processing, particularly digital image processing, ringing artifacts are Artifact (error), artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near Transient (acoustics), transients, particularly sounds from percussion instruments; most noticeable are the pre-echos. The term "ringing" is because the output signal oscillates at a fading rate around a sharp transition in the input, similar to a Bell (instrument), bell after being struck. As with other artifacts, their minimization is a criterion in filter design. Introduction The main cause of ringing artifacts is due to a signal being bandlimited (specifically, not having high frequencies) or passed through a low-pass filter; this is the frequency domain description. In terms of the time domain, the cause of this type of ringing is the ripples in the sinc function,, section I.6, Enhancement: Frequency Doma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clipping (signal Processing)
Clipping is a form of distortion that limits a signal once it exceeds a threshold. Clipping may occur when a signal is recorded by a sensor that has constraints on the range of data it can measure, it can occur when a signal is digitized, or it can occur any other time an analog or digital signal is transformed, particularly in the presence of gain or overshoot and undershoot. Clipping may be described as hard, in cases where the signal is strictly limited at the threshold, producing a flat cutoff; or it may be described as soft, in cases where the clipped signal continues to follow the original at a reduced gain. Hard clipping results in many high-frequency harmonics; soft clipping results in fewer higher-order harmonics and intermodulation distortion components. Audio In the frequency domain, clipping produces strong harmonics in the high-frequency range (as the clipped waveform comes closer to a square wave). The extra high-frequency weighting of the signal could ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
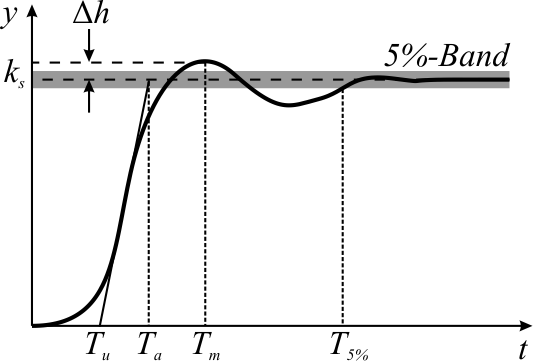
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is the occurrence of a signal or function exceeding its target. Undershoot is the same phenomenon in the opposite direction. It arises especially in the step response of bandlimited systems such as low-pass filters. It is often followed by ringing (signal), ringing, and at times conflated with the latter. Definition Maximum overshoot is defined in Katsuhiko Ogata's ''Discrete-time control systems'' as "the maximum peak value of the response curve measured from the desired response of the system." Control theory In control theory, overshoot refers to an output exceeding its final, steady-state value. For a step response, step input, the ''percentage overshoot'' (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the ''overshoot'' is just the maximum value of the step response minus one. Also see the definition of ''overshoot'' in an #Electronics, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bilinear Filtering
In mathematics, bilinear interpolation is a method for interpolating functions of two variables (e.g., ''x'' and ''y'') using repeated linear interpolation. It is usually applied to functions sampled on a 2D rectilinear grid, though it can be generalized to functions defined on the vertices of (a mesh of) arbitrary convex quadrilaterals. Bilinear interpolation is performed using linear interpolation first in one direction, and then again in another direction. Although each step is linear in the sampled values and in the position, the interpolation as a whole is not linear but rather quadratic in the sample location. Bilinear interpolation is one of the basic resampling techniques in computer vision and image processing, where it is also called bilinear filtering or bilinear texture mapping. Computation Suppose that we want to find the value of the unknown function ''f'' at the point (''x'', ''y''). It is assumed that we know the value of ''f'' at the four points ''Q''11 = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resampling (bitmap)
In computer graphics and digital imaging, image scaling refers to the resizing of a digital image. In video technology, the magnification of digital material is known as upscaling or resolution enhancement. When scaling a vector graphic image, the graphic primitives that make up the image can be scaled using geometric transformations with no loss of image quality. When scaling a raster graphics image, a new image with a higher or lower number of pixels must be generated. In the case of decreasing the pixel number (scaling down), this usually results in a visible quality loss. From the standpoint of digital signal processing, the scaling of raster graphics is a two-dimensional example of sample-rate conversion, the conversion of a discrete signal from a sampling rate (in this case, the local sampling rate) to another. Mathematical Image scaling can be interpreted as a form of image resampling or image reconstruction from the view of the Nyquist sampling theorem. According to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accutance
In photography, acutance describes a subjective perception of visual acuity that is related to the edge contrast of an image. Acutance is related to the magnitude of the gradient of brightness. Due to the nature of the human visual system, an image with higher acutance appears sharper even though an increase in acutance does not increase real resolution. Historically, acutance was enhanced chemically during development of a negative (high acutance developers), or by optical means in printing (unsharp masking). In digital photography, onboard camera software and image postprocessing tools such as Photoshop or GIMP offer various sharpening facilities, the most widely used of which is known as "unsharp mask" because the algorithm is derived from the eponymous analog processing method. In the example image, two light gray lines were drawn on a gray background. As the transition is instantaneous, the line is as sharp as can be represented at this resolution. Acutance in the left ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |