|
Weitzenböck's Inequality
In mathematics, Weitzenböck's inequality, named after Roland Weitzenböck, states that for a triangle of side lengths a, b, c, and area \Delta, the following inequality holds: : a^2 + b^2 + c^2 \geq 4\sqrt\, \Delta. Equality occurs if and only if the triangle is equilateral. Pedoe's inequality is a generalization of Weitzenböck's inequality. The Hadwiger–Finsler inequality is a strengthened version of Weitzenböck's inequality. Geometric interpretation and proof Rewriting the inequality above allows for a more concrete geometric interpretation, which in turn provides an immediate proof. : \fraca^2 + \fracb^2 + \fracc^2 \geq 3\, \Delta. Now the summands on the left side are the areas of equilateral triangles erected over the sides of the original triangle and hence the inequation states that the sum of areas of the equilateral triangles is always greater than or equal to threefold the area of the original triangle. : \Delta_a + \Delta_b + \Delta_c \geq 3\, \Delta. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Napoleon's Triangle
In geometry, Napoleon's theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centres of those equilateral triangles themselves form an equilateral triangle. The triangle thus formed is called the inner or outer ''Napoleon triangle''. The difference in the areas of the outer and inner Napoleon triangles equals the area of the original triangle. The theorem is often attributed to Napoleon Bonaparte (1769–1821). Some have suggested that it may date back to W. Rutherford's 1825 question published in '' The Ladies' Diary'', four years after the French emperor's death, but the result is covered in three questions set in an examination for a Gold Medal at the University of Dublin in October, 1820, whereas Napoleon died the following May. Proofs In the figure above, ABC is the original triangle. AZB, BXC, and CYA are equilateral triangles constructed on its sides' exteriors, and points L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an organized, open-source collection of small (or medium-size) interactive programs called Demonstrations, which are meant to visually and interactively represent ideas from a range of fields. It is hosted by Wolfram Research, whose stated goal is to bring computational exploration to a large population. At its launch, it contained 1300 demonstrations but has grown to over 10,000. The site won a Parents' Choice Award in 2008. Technology The Demonstrations run in ''Mathematica'' 6 or above and in ''CDF Player, Wolfram CDF Player'' which is a free modified version of Wolfram's ''Mathematica'' and available for Windows, Linux and macOS and can operate as a web browser plugin. They typically consist of a very direct user interface to a graphic or visualization, which dynamically recomputes in response to user actions such as moving a slider, clicking a button, or dragging a piece of graphics. Each Demonstration also has a brief descriptio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Göttinger Digitalisierungszentrum
The Center for Retrospective Digitization in Göttingen (german: Göttinger DigitalisierungsZentrum, GDZ) is an online system for archiving academic journals maintained by the University of Göttingen The University of Göttingen, officially the Georg August University of Göttingen, (german: Georg-August-Universität Göttingen, known informally as Georgia Augusta) is a public research university in the city of Göttingen, Germany. Founded .... See also * JSTOR * List of retrodigitized Mathematics Journals and Monograph References External linksOfficial website (German only) German digital libraries Academic publishing Göttingen {{database-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Pedoe
Dan Pedoe (29 October 1910, London – 27 October 1998, St Paul, Minnesota, USA) was an English-born mathematician and geometer with a career spanning more than sixty years. In the course of his life he wrote approximately fifty research and expository papers in geometry. He is also the author of various core books on mathematics and geometry some of which have remained in print for decades and been translated into several languages. These books include the three-volume ''Methods of Algebraic Geometry'' (which he wrote in collaboration with W. V. D. Hodge), ''The Gentle Art of Mathematics'', ''Circles: A Mathematical View'', ''Geometry and the Visual Arts'' and most recently ''Japanese Temple Geometry Problems: San Gaku'' (with Hidetoshi Fukagawa). Early life Daniel Pedoe was born in London in 1910, the youngest of thirteen children of Szmul Abramski, a Jewish immigrant from Poland who found himself in London in the 1890s: he had boarded a cattleboat not knowing whether it was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isoperimetric Inequality
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In n-dimensional space \R^n the inequality lower bounds the surface area or perimeter \operatorname(S) of a set S\subset\R^n by its volume \operatorname(S), :\operatorname(S)\geq n \operatorname(S)^ \, \operatorname(B_1)^, where B_1\subset\R^n is a unit sphere. The equality holds only when S is a sphere in \R^n. On a plane, i.e. when n=2, the isoperimetric inequality relates the square of the circumference of a closed curve and the area of a plane region it encloses. '' Isoperimetric'' literally means "having the same perimeter". Specifically in \R ^2, the isoperimetric inequality states, for the length ''L'' of a closed curve and the area ''A'' of the planar region that it encloses, that : L^2 \ge 4\pi A, and that equality holds if and only if the curve is a circle. The isoperimetric problem is to determine a plane figure of the largest possible area whose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Triangle Inequalities
In geometry, triangle inequalities are inequalities involving the parameters of triangles, that hold for every triangle, or for every triangle meeting certain conditions. The inequalities give an ordering of two different values: they are of the form "less than", "less than or equal to", "greater than", or "greater than or equal to". The parameters in a triangle inequality can be the side lengths, the semiperimeter, the angle measures, the values of trigonometric functions of those angles, the area of the triangle, the medians of the sides, the altitudes, the lengths of the internal angle bisectors from each angle to the opposite side, the perpendicular bisectors of the sides, the distance from an arbitrary point to another point, the inradius, the exradii, the circumradius, and/or other quantities. Unless otherwise specified, this article deals with triangles in the Euclidean plane. Main parameters and notation The parameters most commonly appearing in triangle inequaliti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
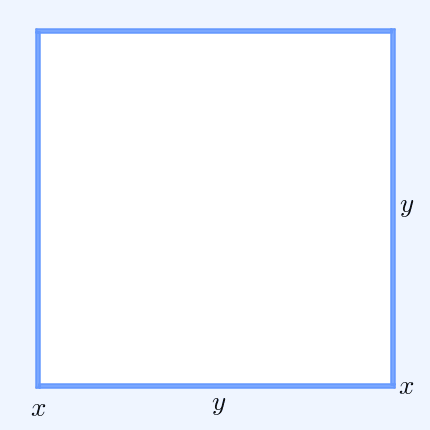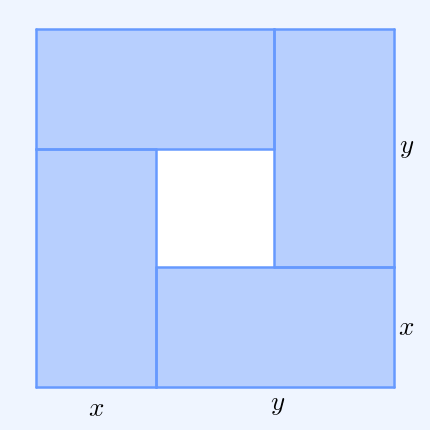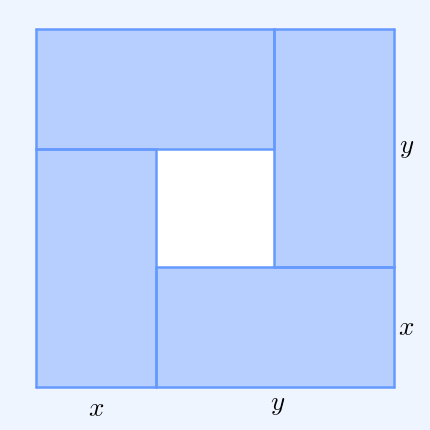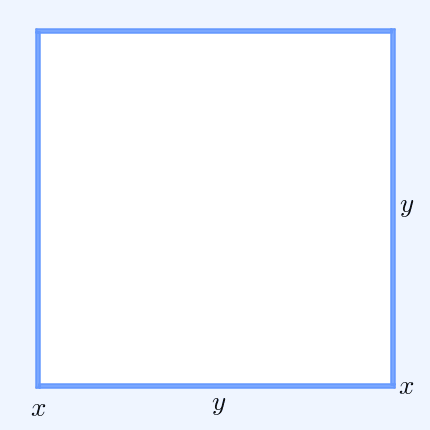
AM–GM Inequality
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers and , is the statement that :\frac2 \ge \sqrt with equality if and only if . This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case of the binomial formula: :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end Hence , with equality precisely when , i.e. . The AM–GM inequality then follows from taking the positive square root of both sides and then dividing bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heron's Formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths , , . If s = \tfrac12(a + b + c) is the semiperimeter of the triangle, the area is, :A = \sqrt. It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work ''Metrica'', though it was probably known centuries earlier. Example Let be the triangle with sides , and . This triangle’s semiperimeter is :s=\frac=\frac=16 and so the area is : \begin A &= \sqrt = \sqrt\\ &= \sqrt = \sqrt = 24. \end In this example, the side lengths and area are integers, making it a Heronian triangle. However, Heron's formula works equally well in cases where one or more of the side lengths are not integers. Alternate expressions Heron's formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways, :\begin A &=\tfrac\sqrt \\ mu&=\tfrac\sqrt \\ mu&=\tfrac\sqrt \\ mu&=\tfrac\sqrt \\ mu&=\tf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hadwiger Finsler Inequality
Hugo Hadwiger (23 December 1908 in Karlsruhe, Germany – 29 October 1981 in Bern, Switzerland) was a Swiss mathematician, known for his work in geometry, combinatorics, and cryptography. Biography Although born in Karlsruhe, Germany, Hadwiger grew up in Bern, Switzerland.. He did his undergraduate studies at the University of Bern, where he majored in mathematics but also studied physics and actuarial science. He continued at Bern for his graduate studies, and received his Ph.D. in 1936 under the supervision of Willy Scherrer. He was for more than forty years a professor of mathematics at Bern. Mathematical concepts named after Hadwiger Hadwiger's theorem in integral geometry classifies the isometry-invariant valuations on compact convex sets in ''d''-dimensional Euclidean space. According to this theorem, any such valuation can be expressed as a linear combination of the intrinsic volumes; for instance, in two dimensions, the intrinsic volumes are the area, the perimete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Mathematical Olympiad
The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980. More than 100 countries, representing over 90% of the world's population, send teams of up to six students, plus one team leader, one deputy leader, and observers. The content ranges from extremely difficult algebra and pre-calculus problems to problems on branches of mathematics not conventionally covered in secondary or high school and often not at university level either, such as projective and complex geometry, functional equations, combinatorics, and well-grounded number theory, of which extensive knowledge of theorems is required. Calculus, though allowed in solutions, is never required, as there is a principle that anyone with a basic understanding of mathematics should understand the problems, even if the solutions requir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |