|
Wiener Deconvolution
In mathematics, Wiener deconvolution is an application of the Wiener filter to the noise problems inherent in deconvolution. It works in the frequency domain, attempting to minimize the impact of deconvolved noise at frequencies which have a poor signal-to-noise ratio. The Wiener deconvolution method has widespread use in image deconvolution applications, as the frequency spectrum of most visual images is fairly well behaved and may be estimated easily. Wiener deconvolution is named after Norbert Wiener. Definition Given a system: :\ y(t) = (h*x)(t) + n(t) where * denotes convolution and: *\ x(t) is some original signal (unknown) at time \ t . *\ h(t) is the known impulse response of a linear time-invariant system *\ n(t) is some unknown additive noise, independent of \ x(t) *\ y(t) is our observed signal Our goal is to find some \ g(t) so that we can estimate \ x(t) as follows: :\ \hat(t) = (g*y)(t) where \ \hat(t) is an estimate of \ x(t) that minimizes the mean square ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Restoration (motion Blur, Wiener Filtering)
Image restoration is the operation of taking a corrupt/noisy image and estimating the clean, original image. Corruption may come in many forms such as motion blur, noise and camera mis-focus. Image restoration is performed by reversing the process that blurred the image and such is performed by imaging a point source and use the point source image, which is called the Point Spread Function (PSF) to restore the image information lost to the blurring process. Image restoration is different from image enhancement in that the latter is designed to emphasize features of the image that make the image more pleasing to the observer, but not necessarily to produce realistic data from a scientific point of view. Image enhancement techniques (like contrast stretching or de-blurring by a nearest neighbor procedure) provided by imaging packages use no ''a priori'' model of the process that created the image. With image enhancement noise can effectively be removed by sacrificing some resolution, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to end th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blind Deconvolution
In electrical engineering and applied mathematics, blind deconvolution is deconvolution without explicit knowledge of the impulse response function used in the convolution. This is usually achieved by making appropriate assumptions of the input to estimate the impulse response by analyzing the output. Blind deconvolution is not solvable without making assumptions on input and impulse response. Most of the algorithms to solve this problem are based on assumption that both input and impulse response live in respective known subspaces. However, blind deconvolution remains a very challenging non-convex optimization problem even with this assumption. In image processing In image processing, blind deconvolution is a deconvolution technique that permits recovery of the target scene from a single or set of "blurred" images in the presence of a poorly determined or unknown point spread function (PSF). Regular linear and non-linear deconvolution techniques utilize a known PSF. For blind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deconvolution
In mathematics, deconvolution is the operation inverse to convolution. Both operations are used in signal processing and image processing. For example, it may be possible to recover the original signal after a filter (convolution) by using a deconvolution method with a certain degree of accuracy. Due to the measurement error of the recorded signal or image, it can be demonstrated that the worse the SNR, the worse the reversing of a filter will be; hence, inverting a filter is not always a good solution as the error amplifies. Deconvolution offers a solution to this problem. The foundations for deconvolution and time-series analysis were largely laid by Norbert Wiener of the Massachusetts Institute of Technology in his book ''Extrapolation, Interpolation, and Smoothing of Stationary Time Series'' (1949). The book was based on work Wiener had done during World War II but that had been classified at the time. Some of the early attempts to apply these theories were in the fields of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
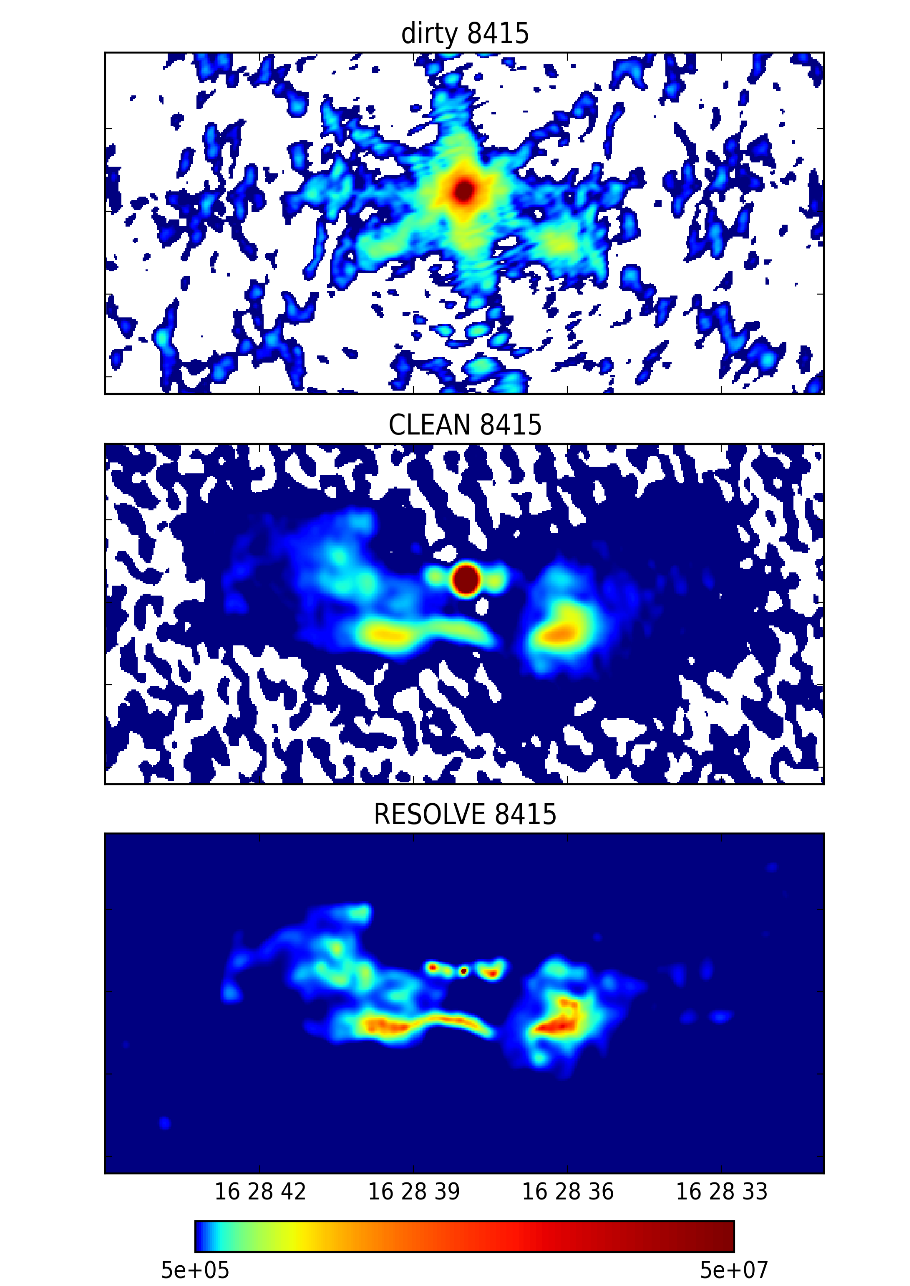
Information Field Theory
Information field theory (IFT) is a Bayesian statistical field theory relating to signal reconstruction, cosmography, and other related areas. IFT summarizes the information available on a physical field using Bayesian probabilities. It uses computational techniques developed for quantum field theory and statistical field theory to handle the infinite number of degrees of freedom of a field and to derive algorithms for the calculation of field expectation values. For example, the posterior expectation value of a field generated by a known Gaussian process and measured by a linear device with known Gaussian noise statistics is given by a generalized Wiener filter applied to the measured data. IFT extends such known filter formula to situations with nonlinear physics, nonlinear devices, non-Gaussian field or noise statistics, dependence of the noise statistics on the field values, and partly unknown parameters of measurement. For this it uses Feynman diagrams, renormalisation fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wirtinger Derivatives
In complex analysis of one and several complex variables, Wirtinger derivatives (sometimes also called Wirtinger operators), named after Wilhelm Wirtinger who introduced them in 1927 in the course of his studies on the theory of functions of several complex variables, are partial differential operators of the first order which behave in a very similar manner to the ordinary derivatives with respect to one real variable, when applied to holomorphic functions, antiholomorphic functions or simply differentiable functions on complex domains. These operators permit the construction of a differential calculus for such functions that is entirely analogous to the ordinary differential calculus for functions of real variables. Historical notes Early days (1899–1911): the work of Henri Poincaré Wirtinger derivatives were used in complex analysis at least as early as in the paper , as briefly noted by and by . As a matter of fact, in the third paragraph of his 1899 paper, Henri Poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parseval's Theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum (or integral) of the square of a function is equal to the sum (or integral) of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later applied to the Fourier series. It is also known as Rayleigh's energy theorem, or Rayleigh's identity, after John William Strutt, Lord Rayleigh. Although the term "Parseval's theorem" is often used to describe the unitarity of ''any'' Fourier transform, especially in physics, the most general form of this property is more properly called the Plancherel theorem. Statement of Parseval's theorem Suppose that A(x) and B(x) are two complex-valued functions on \mathbb of period 2 \pi that are square integrable (with respect to the Lebesgue measure) over intervals of period length, with Fourier series :A(x)=\sum_^\infty a_ne^ and :B(x)=\sum_^\infty b_ne^ respective ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plancherel Theorem
In mathematics, the Plancherel theorem (sometimes called the Parseval–Plancherel identity) is a result in harmonic analysis, proven by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum. That is, if f(x) is a function on the real line, and \widehat(\xi) is its frequency spectrum, then A more precise formulation is that if a function is in both Lp spaces L^1(\mathbb) and L^2(\mathbb), then its Fourier transform is in L^2(\mathbb), and the Fourier transform map is an isometry with respect to the ''L''2 norm. This implies that the Fourier transform map restricted to L^1(\mathbb) \cap L^2(\mathbb) has a unique extension to a linear isometric map L^2(\mathbb) \mapsto L^2(\mathbb), sometimes called the Plancherel transform. This isometry is actually a unitary map. In effect, this makes it possible to speak of Fourier transforms of quadratically integrable functions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Fourier Transform
In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively it may be viewed as the statement that if we know all frequency and phase information about a wave then we may reconstruct the original wave precisely. The theorem says that if we have a function f:\R \to \Complex satisfying certain conditions, and we use the convention for the Fourier transform that :(\mathcalf)(\xi):=\int_ e^ \, f(y)\,dy, then :f(x)=\int_ e^ \, (\mathcalf)(\xi)\,d\xi. In other words, the theorem says that :f(x)=\iint_ e^ \, f(y)\,dy\,d\xi. This last equation is called the Fourier integral theorem. Another way to state the theorem is that if R is the flip operator i.e. (Rf)(x) := f(-x), then :\mathcal^=\mathcalR=R\mathcal. The theorem holds if both f and its Fourier transform are absolutely integrable (in the Lebesgue sense) and f is continuous at the point x. However, even under more general ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where dagger (†) is used for the conjugate tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Spectral Density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)