 |
Blind Deconvolution
In electrical engineering and applied mathematics, blind deconvolution is deconvolution without explicit knowledge of the impulse response function used in the convolution. This is usually achieved by making appropriate assumptions of the input to estimate the impulse response by analyzing the output. Blind deconvolution is not solvable without making assumptions on input and impulse response. Most of the algorithms to solve this problem are based on assumption that both input and impulse response live in respective known subspaces. However, blind deconvolution remains a very challenging non-convex optimization problem even with this assumption. In image processing In image processing, blind deconvolution is a deconvolution technique that permits recovery of the target scene from a single or set of "blurred" images in the presence of a poorly determined or unknown point spread function (PSF). Regular linear and non-linear deconvolution techniques utilize a known PSF. For blind de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Electrical Engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the latter half of the 19th century after the commercialization of the electric telegraph, the telephone, and electrical power generation, distribution, and use. Electrical engineering is divided into a wide range of different fields, including computer engineering, systems engineering, power engineering, telecommunications, radio-frequency engineering, signal processing, instrumentation, photovoltaic cells, electronics, and optics and photonics. Many of these disciplines overlap with other engineering branches, spanning a huge number of specializations including hardware engineering, power electronics, Electromagnetism, electromagnetics and waves, microwave engineering, nanotechnology, electrochemistry, renewable energies, mechatronics/control ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Reverberation
In acoustics, reverberation (commonly shortened to reverb) is a persistence of sound after it is produced. It is often created when a sound is reflection (physics), reflected on surfaces, causing multiple reflections that build up and then decay as the sound is absorbed by the surfaces of objects in the space – which could include furniture, people, and air. This is most noticeable when the sound source stops but the reflections continue, their amplitude decreasing, until zero is reached. Reverberation is frequency dependent: the length of the decay, or reverberation time, receives special consideration in the architectural design of spaces which need to have specific reverberation times to achieve optimum performance for their intended activity. In comparison to a distinct echo, that is detectable at a minimum of 50 to 100 millisecond, ms after the previous sound, reverberation is the occurrence of reflections that arrive in a sequence of less than approximately 50 ms. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Blur Img
Blur, Blurry, Blurring, Blurred or Blurr, may refer to: Optics and images * Bokeh, the aesthetic quality of the out-of-focus parts of an image * Box blur, a graphic-art effect * Deblurring, process of removing blurring artifacts from images * Defocus aberration, blurring of an image due to incorrect focus * Fogging (censorship), censored blurring * Gaussian blur, a graphic-art effect * Motion blur, blurring of an image due to movement of the subject or imaging system Arts, entertainment, and media Fictional characters * Red Blue Blur, or The Blur, an alternate identity for Clark Kent in ''Smallville'' * The Atlanta Blur or The Blur, a character in the Marvel MAX comic Supreme Power * Blurr (Transformers), ''Transformers'' fictional robot superheroes Films * ''Blurred'' (film), a 2002 Australian film * ''Blurs'' (film), a 2011 Croatian film * ''Blurr'', a 2022 Indian horror thriller film by Ajay Bahl Music * Blur (band), an English rock band Albums * ''Blur'' (Blur album), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Original Img
Originality is the aspect of created or invented works that distinguish them from reproductions, clones, forgeries, or substantially derivative works. The modern idea of originality is according to some scholars tied to Romanticism, by a notion that is often called romantic originality.Smith (1924)Waterhouse (1926)Macfarlane (2007) The validity of "originality" as an operational concept has been questioned. For example, there is no clear boundary between "derivative" and "inspired by" or "in the tradition of." The concept of originality is both culturally and historically contingent. For example, unattributed reiteration of a published text in one culture might be considered plagiarism but in another culture might be regarded as a convention of veneration. At the time of Shakespeare, it was more common to appreciate the similarity with an admired classical work, and Shakespeare himself avoided "unnecessary invention".Royal Shakespeare Company (2007) ''The RSC Shakespeare - Will ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
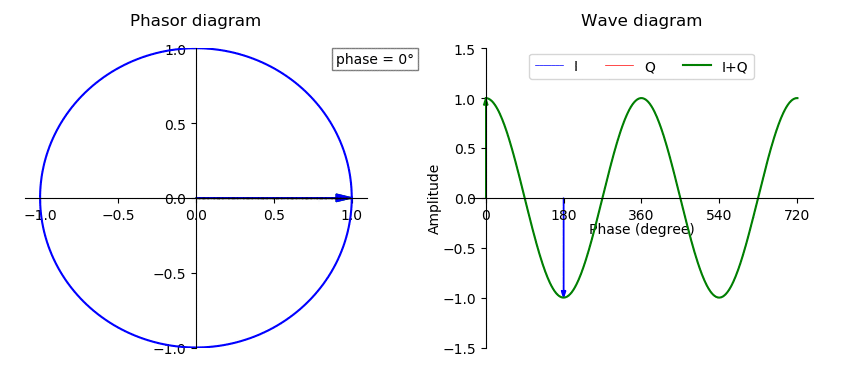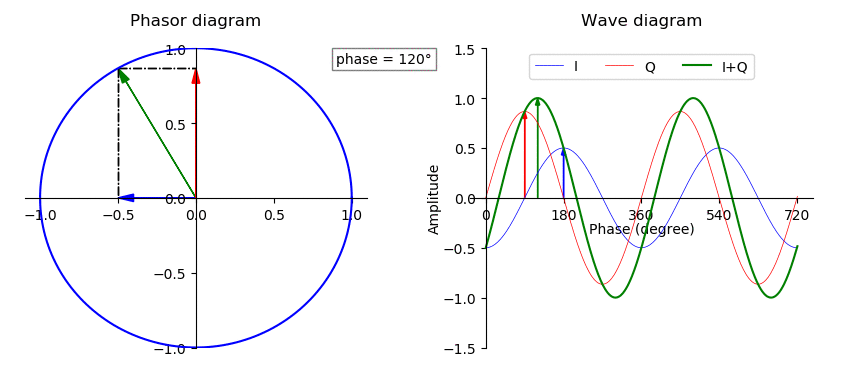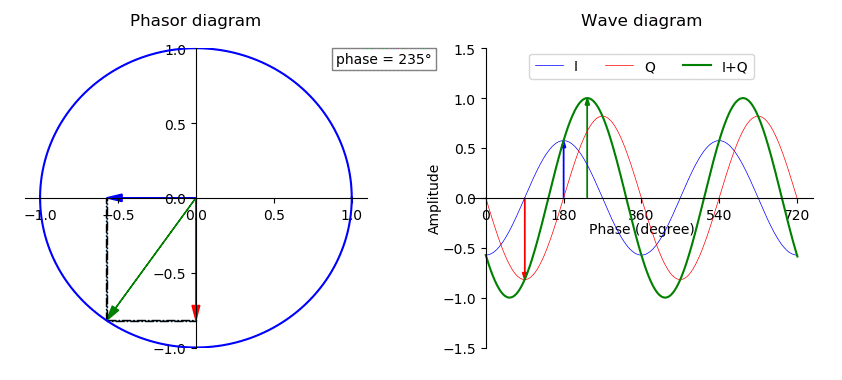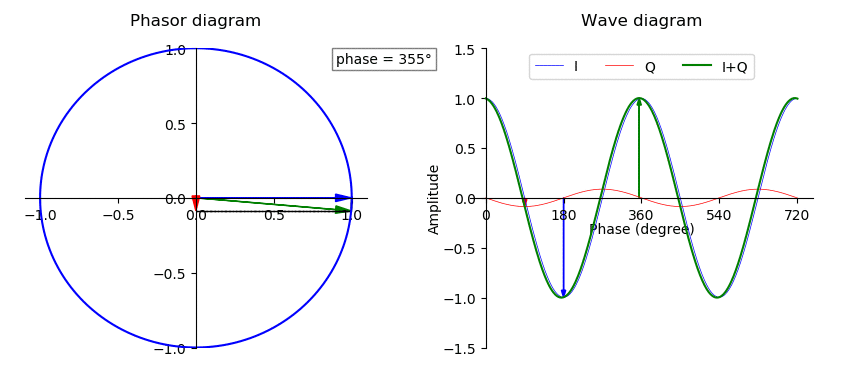
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Whitening Transform
A whitening transformation or sphering transformation is a linear transformation that transforms a vector of random variables with a known covariance matrix into a set of new variables whose covariance is the identity matrix, meaning that they are uncorrelated and each have variance 1. The transformation is called "whitening" because it changes the input vector into a white noise vector. Several other transformations are closely related to whitening: # the decorrelation transform removes only the correlations but leaves variances intact, # the standardization transform sets variances to 1 but leaves correlations intact, # a coloring transformation transforms a vector of white random variables into a random vector with a specified covariance matrix. Definition Suppose X is a random (column) vector with non-singular covariance matrix \Sigma and mean 0. Then the transformation Y = W X with a whitening matrix W satisfying the condition W^\mathrm W = \Sigma^ yields the whitened ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Auto Correlation
Autocorrelation, sometimes known as serial correlation in the discrete time case, measures the correlation of a signal with a delayed copy of itself. Essentially, it quantifies the similarity between observations of a random variable at different points in time. The analysis of autocorrelation is a mathematical tool for identifying repeating patterns or hidden periodicities within a signal obscured by noise. Autocorrelation is widely used in signal processing, time domain and time series analysis to understand the behavior of data over time. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Various time series models incorporate autocorrelation, such as unit root processes, trend-stationary processes, autoregressive processes, and moving average processes. Autocorrelation of stochastic processes In statistics, the autocorrelation of a real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
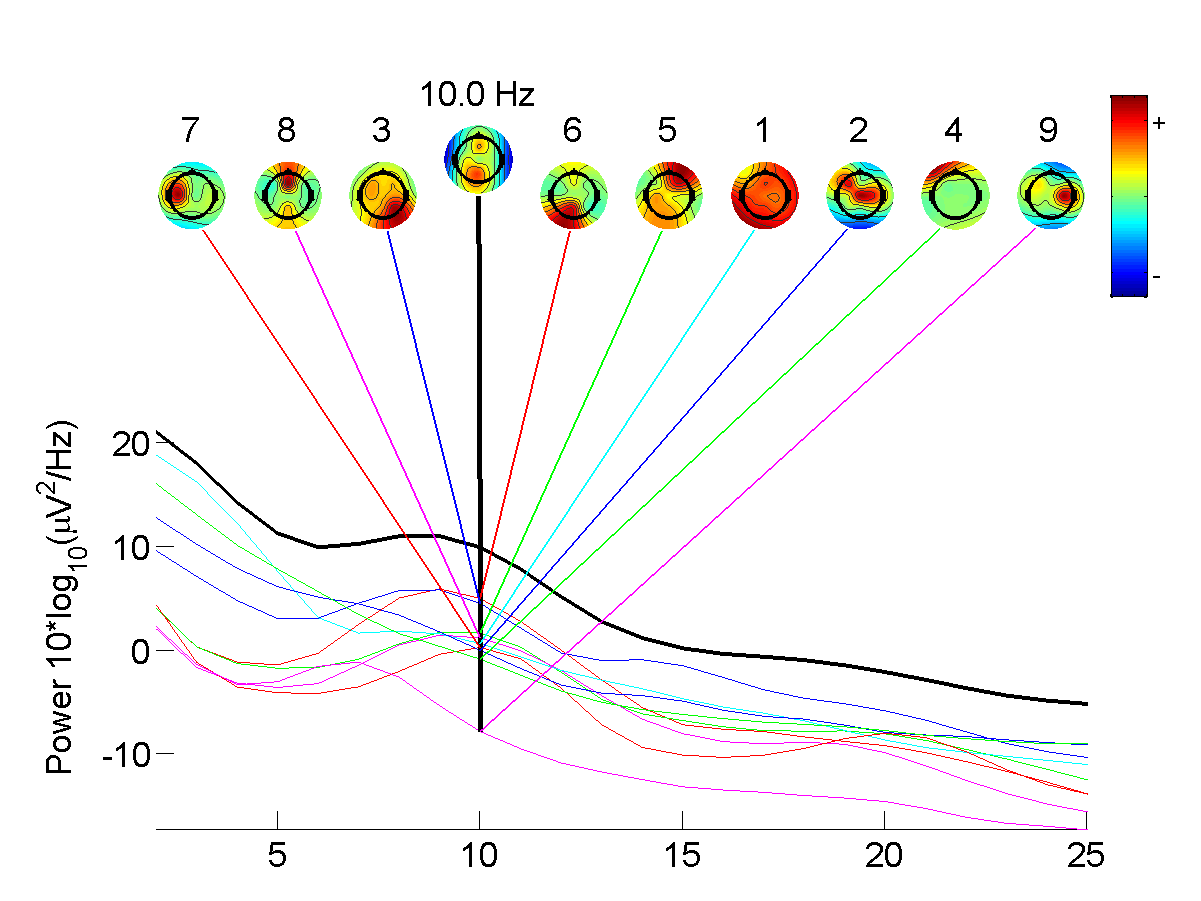
Spectral Power Density
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectral energy distribution that would be f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Wiener Filter
In signal processing, the Wiener filter is a filter used to produce an estimate of a desired or target random process by linear time-invariant ( LTI) filtering of an observed noisy process, assuming known stationary signal and noise spectra, and additive noise. The Wiener filter minimizes the mean square error between the estimated random process and the desired process. Description The goal of the wiener filter is to compute a statistical estimate of an unknown signal using a related signal as an input and filtering it to produce the estimate. For example, the known signal might consist of an unknown signal of interest that has been corrupted by additive noise. The Wiener filter can be used to filter out the noise from the corrupted signal to provide an estimate of the underlying signal of interest. The Wiener filter is based on a statistical approach, and a more statistical account of the theory is given in the minimum mean square error (MMSE) estimator article. Typical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Recovered Img
Recovered is a behavioral health organization focused on alcoholism, drug addiction and the consequences of alcohol and other drug use. Overview Recovered is an online platform for people seeking treatment for substance use disorder and other mental health conditions in the United States. Their directory lists over 15,000 treatment facilities across the country, including those offering residential inpatient care, outpatient programs, detox centers, and medication-assisted treatment options. They also offer resources for those seeking support groups or mental health counseling and are listed as a peer support resource by the Substance Abuse and Mental Health Services Administration (SAMHSA). History In April 2021 the NCADD website was acquired by JBKM Ltd. In December 2021 the website was relaunched under its new brand name, Recovered. In July 2023, Recovered launched the "Recovered Trustscore", an independent rating system for rehab centers "designed to rank all rehab cente ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Equalization (communications)
In telecommunication, equalization is the reversal of distortion incurred by a signal transmitted through a channel. Equalizers are used to render the frequency response—for instance of a telephone line—''flat'' from end-to-end. When a channel has been equalized the frequency domain attributes of the signal at the input are faithfully reproduced at the output. Telephones, DSL lines and television cables use equalizers to prepare data signals for transmission. Equalizers are critical to the successful operation of electronic systems such as analog broadcast television. In this application the actual waveform of the transmitted signal must be preserved, not just its frequency content. Equalizing filters must cancel out any group delay and phase delay between different frequency components. Analog telecommunications Audio lines Early telephone systems used equalization to correct for the reduced level of high frequencies in long cables, typically using Zobel networks. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |