|
Weyl Differintegral
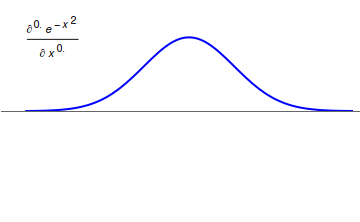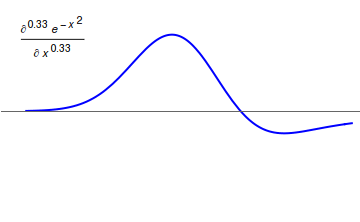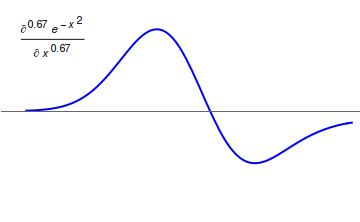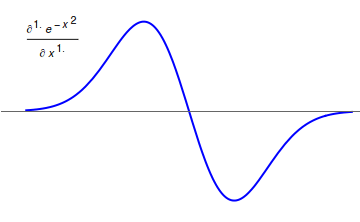
In mathematics, the Weyl integral (named after Hermann Weyl) is an operator defined, as an example of fractional calculus, on functions ''f'' on the unit circle having integral 0 and a Fourier series. In other words there is a Fourier series for ''f'' of the form : \sum_^ a_n e^ with ''a''0 = 0. Then the Weyl integral operator of order ''s'' is defined on Fourier series by : \sum_^ (in)^s a_n e^ where this is defined. Here ''s'' can take any real value, and for integer values ''k'' of ''s'' the series expansion is the expected ''k''-th derivative, if ''k'' > 0, or (−''k'')th indefinite integral normalized by integration from ''θ'' = 0. The condition ''a''0 = 0 here plays the obvious role of excluding the need to consider division by zero. The definition is due to Hermann Weyl (1917). See also *Sobolev space In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermann Weyl
Hermann Klaus Hugo Weyl, (; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, he is associated with the University of Göttingen tradition of mathematics, represented by Carl Friedrich Gauss, David Hilbert and Hermann Minkowski. His research has had major significance for theoretical physics as well as purely mathematical disciplines such as number theory. He was one of the most influential mathematicians of the twentieth century, and an important member of the Institute for Advanced Study during its early years. Weyl contributed to an exceptionally wide range of mathematical fields, including works on space, time, matter, philosophy, logic, symmetry and the history of mathematics. He was one of the first to conceive of combining general relativity with the laws of electromagnetism. Freeman Dyson wrote that Weyl alone bore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dista ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or ''period''), the number of components, and their amplitudes and phase parameters. With appropriate choices, one cycle (or ''period'') of the summation can be made to approximate an arbitrary function in that interval (or the entire function if it too is periodic). The number of components is theoretically infinite, in which case the other parameters can be chosen to cause the series to converge to almost any ''well behaved'' periodic function (see Pathological and Dirichlet–Jordan test). The components of a particular function are determined by ''analysis'' techniques described in this article. Sometimes the components are known first, and the unknown function is ''synthesized'' by a Fourier series. Such is the case of a discrete-ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sobolev Space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of ''Lp''-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function. Sobolev spaces are named after the Russian mathematician Sergei Sobolev. Their importance comes from the fact that weak solutions of some important partial differential equations exist in appropriate Sobolev spaces, even when there are no strong solutions in spaces of continuous functions with the derivatives understood in the classical sense. Motivation In this section and throughout the article \Omega is an open subset of \R^n. There are many c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
