|
Variational Principle
A variational principle is a mathematical procedure that renders a physical problem solvable by the calculus of variations, which concerns finding functions that optimize the values of quantities that depend on those functions. For example, the problem of determining the shape of a hanging chain suspended at both ends—a catenary—can be solved using variational calculus, and in this case, the variational principle is the following: The solution is a function that minimizes the gravitational potential energy of the chain. History Physics The history of the variational principle in classical mechanics started with Maupertuis's principle in the 18th century. Math Felix Klein's 1872 Erlangen program attempted to identify invariants under a group of transformations. Examples In mathematics * Ekeland's variational principle in mathematical optimization * The finite element method * The variation principle relating topological entropy and Kolmogorov-Sinai entropy. In physics * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calculus Of Variations
The calculus of variations (or variational calculus) is a field of mathematical analysis that uses variations, which are small changes in Function (mathematics), functions and functional (mathematics), functionals, to find maxima and minima of functionals: Map (mathematics), mappings from a set of Function (mathematics), functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometrical Optics
Geometrical optics, or ray optics, is a model of optics that describes light Wave propagation, propagation in terms of ''ray (optics), rays''. The ray in geometrical optics is an abstract object, abstraction useful for approximating the paths along which light propagates under certain circumstances. The simplifying assumptions of geometrical optics include that light rays: * propagate in straight-line paths as they travel in a Homogeneity (physics), homogeneous medium * bend, and in particular circumstances may split in two, at the Interface (matter), interface between two dissimilar optical medium, media * follow curved paths in a medium in which the refractive index changes * may be absorbed or reflected. Geometrical optics does not account for certain optical effects such as diffraction and Interference (wave propagation), interference, which are considered in physical optics. This simplification is useful in practice; it is an excellent approximation when the wavelength is smal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
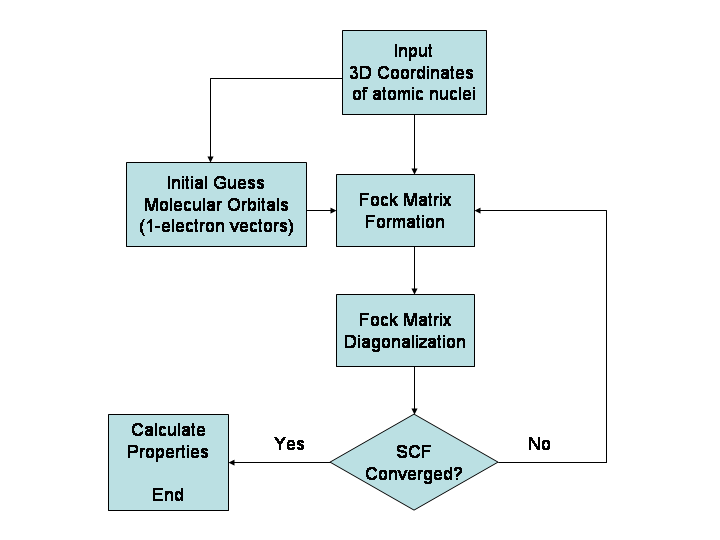
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Palatini Variation
In general relativity and gravitation the Palatini variation is nowadays thought of as a variation of a Lagrangian with respect to the connection. In fact, as is well known, the Einstein–Hilbert action for general relativity was first formulated purely in terms of the spacetime metric . In the Palatini variational method one takes as independent field variables not only the ten components but also the forty components of the affine connection , assuming, a priori, no dependence of the from the and their derivatives. The reason the Palatini variation is considered important is that it means that the use of the Christoffel connection in general relativity does not have to be added as a separate assumption; the information is already in the Lagrangian. For theories of gravitation which have more complex Lagrangians than the Einstein–Hilbert Lagrangian of general relativity, the Palatini variation sometimes gives more complex connections and sometimes tensorial equations. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Einstein Field Equations
In the General relativity, general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of Matter#In general relativity and cosmology, matter within it. The equations were published by Albert Einstein in 1915 in the form of a Tensor, tensor equation which related the local ' (expressed by the Einstein tensor) with the local energy, momentum and stress within that spacetime (expressed by the stress–energy tensor). Analogously to the way that electromagnetic fields are related to the distribution of Charge (physics), charges and Electric current, currents via Maxwell's equations, the EFE relate the spacetime geometry to the distribution of mass–energy, momentum and stress, that is, they determine the Metric tensor (general relativity), metric tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Ei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Einstein–Hilbert Action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the stationary-action principle. With the metric signature, the gravitational part of the action is given as :S = \int R \sqrt \, \mathrm^4x, where g=\det(g_) is the determinant of the metric tensor matrix, R is the Ricci scalar, and \kappa = 8\pi Gc^ is the Einstein gravitational constant (G is the gravitational constant and c is the speed of light in vacuum). If it converges, the integral is taken over the whole spacetime. If it does not converge, S is no longer well-defined, but a modified definition where one integrates over arbitrarily large, relatively compact domains, still yields the Einstein equation as the Euler–Lagrange equation of the Einstein–Hilbert action. The action was proposed by David Hilbert in 1915 as part of his application of the variational principle to a combination of gravity and electromagnetism. Discussion Deriving equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gauss's Principle Of Least Constraint
The principle of least constraint is one variational formulation of classical mechanics enunciated by Carl Friedrich Gauss in 1829, equivalent to all other formulations of analytical mechanics. Intuitively, it says that the acceleration of a constrained physical system will be as similar as possible to that of the corresponding unconstrained system. Statement The principle of least constraint is a least squares principle stating that the true accelerations of a mechanical system of n masses is the minimum of the quantity : Z \, \stackrel \sum_^ m_j \cdot \left, \, \ddot \mathbf_j - \frac \^ where the ''j''th particle has mass m_j, position vector \mathbf_j, and applied non-constraint force \mathbf_j acting on the mass. The notation \dot \mathbf indicates time derivative of a vector function \mathbf(t), i.e. position. The corresponding accelerations \ddot \mathbf_j satisfy the imposed constraints, which in general depends on the current state of the system, \. It is reca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hellmann–Feynman Theorem
In quantum mechanics, the Hellmann–Feynman theorem relates the derivative of the total energy with respect to a parameter to the expectation value of the derivative of the Hamiltonian with respect to that same parameter. According to the theorem, once the spatial distribution of the electrons has been determined by solving the Schrödinger equation, all the forces in the system can be calculated using classical electrostatics. The theorem has been proven independently by many authors, including Paul Güttinger (1932), Wolfgang Pauli (1933), Hans Hellmann (1937) and Richard Feynman (1939). The theorem states where *\hat_ is a Hermitian operator depending upon a continuous parameter \lambda\,, *, \psi_\lambda\rangle, is an eigenstate (eigenfunction) of the Hamiltonian, depending implicitly upon \lambda, *E_\, is the energy (eigenvalue) of the state , \psi_\lambda\rangle, i.e. \hat_, \psi_\lambda\rangle = E_, \psi_\lambda\rangle. Note that there is a breakdown of the Hellma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Variational Method (quantum Mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states. This allows calculating approximate wavefunctions such as molecular orbitals. The basis for this method is the variational principle. The method consists of choosing a "trial wavefunction" depending on one or more parameters, and finding the values of these parameters for which the expectation value of the energy is the lowest possible. The wavefunction obtained by fixing the parameters to such values is then an approximation to the ground state wavefunction, and the expectation value of the energy in that state is an upper bound to the ground state energy. The Hartree–Fock method, density matrix renormalization group, and Ritz method apply the variational method. Description Suppose we are given a Hilbert space and a Hermitian operator over it called the Hamiltonian H . Ignoring complications about continuous spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Electromagnetic Theory
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electrostatics and magnetism, which are distinct but closely intertwined phenomena. Electromagnetic forces occur between any two charged particles. Electric forces cause an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs between charged particles in relative motion. These two forces are described in terms of electromagnetic fields. Macroscopic charged objects are described in terms of Coulomb's law for electricity and Ampère's force law for magnetism; the Lorentz force describes microscopic charged particles. The electromagnetic force is responsible for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo Galilei, Johannes Kepler, Christiaan Huygens, and Isaac Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum realm. History ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |