|
Von Staudt–Clausen Theorem
In number theory, the von Staudt–Clausen theorem is a result determining the fractional part of Bernoulli numbers, found independently by and . Specifically, if ''n'' is a positive integer and we add 1/''p'' to the Bernoulli number ''B''2''n'' for every prime ''p'' such that ''p'' − 1 divides 2''n'', we obtain an integer, i.e., B_ + \sum_ \frac1p \in \Z . This fact immediately allows us to characterize the denominators of the non-zero Bernoulli numbers ''B''2''n'' as the product of all primes ''p'' such that ''p'' − 1 divides 2''n''; consequently the denominators are square-free and divisible by 6. These denominators are : 6, 30, 42, 30, 66, 2730, 6, 510, 798, 330, 138, 2730, 6, 870, 14322, 510, 6, 1919190, 6, 13530, ... . The sequence of integers B_ + \sum_ \frac1p is : 1, 1, 1, 1, 1, 1, 2, -6, 56, -528, 6193, -86579, 1425518, -27298230, ... . Proof A proof of the Von Staudt–Clausen theorem follows from an explicit formula for Bernoulli numbers which is: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
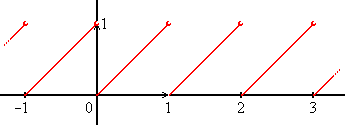
Fractional Part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. If the latter is defined as the largest integer not greater than , called floor of or \lfloor x\rfloor, its fractional part can be written as: :\operatorname (x)=x - \lfloor x \rfloor,\; x > 0. For a positive number written in a conventional positional numeral system (such as binary or decimal), its fractional part hence corresponds to the digits appearing after the radix point. The result is a real number in the half-open interval x, -\lfloor , x, \rfloor , or by the Weisstein,_Eric_W._"Fractional_Part."_From_MathWorld--A_Wolfram_Web_Resource /ref> : |
Bernoulli Number
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of ''m''-th powers of the first ''n'' positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function. The values of the first 20 Bernoulli numbers are given in the adjacent table. Two conventions are used in the literature, denoted here by B^_n and B^_n; they differ only for , where B^_1=-1/2 and B^_1=+1/2. For every odd , . For every even , is negative if is divisible by 4 and positive otherwise. The Bernoulli numbers are special values of the Bernoulli polynomials B_n(x), with B^_n=B_n(0) and B^+_n=B_n(1). The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jacob Bernoulli, after whom they are named, and indepe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square-free Integer
In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, is square-free, but is not, because 18 is divisible by . The smallest positive square-free numbers are Square-free factorization Every positive integer n can be factored in a unique way as n=\prod_^k q_i^i, where the q_i different from one are square-free integers that are pairwise coprime. This is called the ''square-free factorization'' of . To construct the square-free factorization, let n=\prod_^h p_j^ be the prime factorization of n, where the p_j are distinct prime numbers. Then the factors of the square-free factorization are defined as q_i=\prod_p_j. An integer is square-free if and only if q_i=1 for all i > 1. An integer greater than one is the kth power of another integer if and only if k is a divisor of all i such that q_i\neq 1. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stirling Numbers Of The Second Kind
In mathematics, particularly in combinatorics, a Stirling number of the second kind (or Stirling partition number) is the number of ways to partition a set of ''n'' objects into ''k'' non-empty subsets and is denoted by S(n,k) or \textstyle \left\. Stirling numbers of the second kind occur in the field of mathematics called combinatorics and the study of partitions. Stirling numbers of the second kind are one of two kinds of Stirling numbers, the other kind being called Stirling numbers of the first kind (or Stirling cycle numbers). Mutually inverse (finite or infinite) triangular matrices can be formed from the Stirling numbers of each kind according to the parameters ''n'', ''k''. Definition The Stirling numbers of the second kind, written S(n,k) or \lbrace\textstyle\rbrace or with other notations, count the number of ways to partition a set of n labelled objects into k nonempty unlabelled subsets. Equivalently, they count the number of different equivalence relations with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat's Little Theorem
Fermat's little theorem states that if ''p'' is a prime number, then for any integer ''a'', the number a^p - a is an integer multiple of ''p''. In the notation of modular arithmetic, this is expressed as : a^p \equiv a \pmod p. For example, if = 2 and = 7, then 27 = 128, and 128 − 2 = 126 = 7 × 18 is an integer multiple of 7. If is not divisible by , that is if is coprime to , Fermat's little theorem is equivalent to the statement that is an integer multiple of , or in symbols: : a^ \equiv 1 \pmod p. For example, if = 2 and = 7, then 26 = 64, and 64 − 1 = 63 = 7 × 9 is thus a multiple of 7. Fermat's little theorem is the basis for the Fermat primality test and is one of the fundamental results of elementary number theory. The theorem is named after Pierre de Fermat, who stated it in 1640. It is called the "little theorem" to distinguish it from Fermat's Last Theorem.. History Pierre de Fermat first stated the theorem in a letter dated October ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floor And Ceiling Functions
In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or . For example, , , , and . Historically, the floor of has been–and still is–called the integral part or integer part of , often denoted (as well as a variety of other notations). Some authors may define the integral part as if is nonnegative, and otherwise: for example, and . The operation of truncation generalizes this to a specified number of digits: truncation to zero significant digits is the same as the integer part. For an integer, . Notation The ''integral part'' or ''integer part'' of a number ( in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula. Carl Friedrich Gauss introduced the square bracket notation in his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kummer's Congruence
In mathematics, Kummer's congruences are some congruences involving Bernoulli numbers, found by . used Kummer's congruences to define the p-adic zeta function. Statement The simplest form of Kummer's congruence states that : \frac\equiv \frac \pmod p \text h\equiv k \pmod where ''p'' is a prime, ''h'' and ''k'' are positive even integers not divisible by ''p''−1 and the numbers ''B''''h'' are Bernoulli numbers. More generally if ''h'' and ''k'' are positive even integers not divisible by ''p'' − 1, then : (1-p^)\frac\equiv (1-p^)\frac \pmod whenever : h\equiv k\pmod where φ(''p''''a''+1) is the Euler totient function, evaluated at ''p''''a''+1 and ''a'' is a non negative integer. At ''a'' = 0, the expression takes the simpler form, as seen above. The two sides of the Kummer congruence are essentially values of the p-adic zeta function, and the Kummer congruences imply that the ''p''-adic zeta function for negative integers is continuous, so can be extended by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomische Nachrichten
''Astronomische Nachrichten'' (''Astronomical Notes''), one of the first international journals in the field of astronomy, was established in 1821 by the German astronomer Heinrich Christian Schumacher. It claims to be the oldest astronomical journal in the world that is still being published. The publication today specializes in articles on solar physics, extragalactic astronomy, cosmology, geophysics, and instrumentation for these fields. All articles are subject to peer review. Early history The journal was founded in 1821 by Heinrich Christian Schumacher,''Publications of the Astronomical Society of the Pacific'', page 60, v.7 (1895) under the patronage of Christian VIII of Denmark, and quickly became the world's leading professional publication for the field of astronomy. Schumacher edited the journal at the Altona Observatory, then under the administration of Denmark, later part of Prussia, and today part of the German city of Hamburg. Schumacher edited the first 31 issue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
