|
Ultraparallel
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P'' not on ''R'', in the plane containing both line ''R'' and point ''P'' there are at least two distinct lines through ''P'' that do not intersect ''R''. (Compare the above with Playfair's axiom, the modern version of Euclid's parallel postulate.) Hyperbolic plane geometry is also the geometry of pseudospherical surfaces, surfaces with a constant negative Gaussian curvature. Saddle surfaces have negative Gaussian curvature in at least some regions, where they locally resemble the hyperbolic plane. A modern use of hyperbolic geometry is in the theory of special relativity, particularly the Minkowski model. When geometers first realised they were working with something other than the standard Euclidean geometry, they described their geomet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
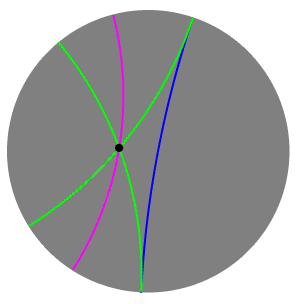
Ultraparallel Theorem
In hyperbolic geometry, two lines may intersect, be ultraparallel, or be limiting parallel. The ultraparallel theorem states that every pair of (distinct) ultraparallel lines has a unique common perpendicular (a hyperbolic line which is perpendicular to both lines). Hilbert's construction Let r and s be two ultraparallel lines. From any two distinct points A and C on s draw AB and CB' perpendicular to r with B and B' on r. If it happens that AB = CB', then the desired common perpendicular joins the midpoints of AC and BB' (by the symmetry of the Saccheri quadrilateral ACB'B). If not, we may suppose AB < CB' without loss of generality. Let E be a point on the line s on the opposite side of A from C. Take A' on CB' so that A'B' = AB. Through A' draw a line s' (A'E') on the side closer to E, so that the angle B'A'E' is the same as angle BAE. Then s' meets s in an ordinary point D'. Construct a point D on ray AE so that AD = A'D'. Then D' ≠ D. They are the same distance fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Klein
Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and group theory. His 1872 Erlangen program, classifying geometries by their basic symmetry groups, was an influential synthesis of much of the mathematics of the time. Life Felix Klein was born on 25 April 1849 in Düsseldorf, to Prussian parents. His father, Caspar Klein (1809–1889), was a Prussian government official's secretary stationed in the Rhine Province. His mother was Sophie Elise Klein (1819–1890, née Kayser). He attended the Gymnasium in Düsseldorf, then studied mathematics and physics at the University of Bonn, 1865–1866, intending to become a physicist. At that time, Julius Plücker had Bonn's professorship of mathematics and experimental physics, but by the time Klein became his assistant, in 1866, Plücker's interest wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Point
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space. Given a line ''l'' and a point ''P'' not on ''l'', right- and left-limiting parallels to ''l'' through ''P'' converge to ''l'' at ''ideal points''. Unlike the projective case, ideal points form a boundary, not a submanifold. So, these lines do not intersect at an ideal point and such points, although well-defined, do not belong to the hyperbolic space itself. The ideal points together form the Cayley absolute or boundary of a hyperbolic geometry. For instance, the unit circle forms the Cayley absolute of the Poincaré disk model and the Klein disk model. While the real line forms the Cayley absolute of the Poincaré half-plane model . Pasch's axiom and the exterior angle theorem still hold for an omega triangle, defined by two points in hyperbolic space and an omega point. Properties * The hyperbolic distance between an ideal point and an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limiting Parallel
In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line l through a point P not on line R; however, in the plane, two parallels may be closer to l than all others (one in each direction of R). Thus it is useful to make a new definition concerning parallels in neutral geometry. If there are closest parallels to a given line they are known as the limiting parallel, asymptotic parallel or horoparallel (horo from el, ὅριον — border). For rays, the relation of limiting parallel is an equivalence relation, which includes the equivalence relation of being coterminal. If, in a hyperbolic triangle, the pairs of sides are limiting parallel, then the triangle is an ideal triangle. Definition A ray Aa is a limiting parallel to a ray Bb if they are coterminal or if they lie on distinct lines not equal to the line AB, they do not meet, and every ray in the interior of the angle BAa meets the ray Bb. Properties Distinct lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Models Of The Hyperbolic Plane
A model is an informative representation of an object, person or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin ''modulus'', a measure. Models can be divided into physical models (e.g. a model plane) and abstract models (e.g. mathematical expressions describing behavioural patterns). Abstract or conceptual models are central to philosophy of science, as almost every scientific theory effectively embeds some kind of model of the physical or human sphere. In commerce, "model" can refer to a specific design of a product as displayed in a catalogue or show room (e.g. Ford Model T), and by extension to the sold product itself. Types of models include: Physical model A physical model (most commonly referred to simply as a model but in this context distinguished from a conceptual model) is a smaller or larger physical copy of an object. The object being modelled may be small (for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supplementary Angles
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measure of an angle or of a rotation. This measure is the ratio of the length of a circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation. History and etymology The word ''angle'' comes from the Latin word ''angulus'', meaning "corner"; cognate words are the Greek ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Scale
There is no single definition of an absolute scale. In statistics and measurement theory, it is simply a ratio scale in which the unit of measurement is fixed, and values are obtained by counting. According to another definition it is a system of measurement that begins at a minimum, or zero point, and progresses in only one direction. Yet another definition tells us it is the count of the elements in a set, with its natural origin being zero, the empty set. Some sources tell us that even time can be measured in an absolute scale, proving year zero is measured from the beginning of the universe. How that is obtained precisely would be a matter of debate. The most accepted absolute scale is the Kelvin temperature scale, where absolute zero is the temperature at which molecular energy is at a minimum. Another absolute scale is the Rankine temperature scale. In general, an absolute scale differs from a relative scale in having some reference point that is not arbitrarily selected. Fea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Of Parallelism
In hyperbolic geometry, the angle of parallelism \Pi(a) , is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length ''a'' between the right angle and the vertex of the angle of parallelism. Given a point not on a line, drop a perpendicular to the line from the point. Let ''a'' be the length of this perpendicular segment, and \Pi(a) be the least angle such that the line drawn through the point does not intersect the given line. Since two sides are asymptotically parallel, : \lim_ \Pi(a) = \tfrac\pi\quad\text\quad\lim_ \Pi(a) = 0. There are five equivalent expressions that relate '' \Pi(a)'' and ''a'': : \sin\Pi(a) = \operatorname a = \frac =\frac \ , : \cos\Pi(a) = \tanh a = \frac \ , : \tan\Pi(a) = \operatorname a = \frac = \frac \ , : \tan \left( \tfrac\Pi(a) \right) = e^, : \Pi(a) = \tfrac\pi - \operatorname(a), where sinh, cosh, tanh, sech and cs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. ''Elements'' is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19th century. Euclid's ''Elements'' has been referred to as the most successful and influential textbook ever written. It was one of the very earliest mathematical works to be printed after the invention of the printing press and has been estimated to be second only to the Bible in the number of editions published since the first printing i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Geometry
Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not sufficient as a basis of Euclidean geometry, other systems, such as Hilbert's axioms without the parallel axiom, are used. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate. Properties It might be imagined that absolute geometry is a rather weak system, but that is not the case. Indeed, in Euclid's ''Elements'', the first 28 Propositions and Proposition 31 avoid using the parallel postulate, and therefore are valid in absolute geometry. One can also prove in absolute geometry the exterior angle theorem (an exterior angle of a triangle is larger than either of the remote angles), as well as the Saccheri–Legendre theorem, which states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'. The term has subtle differences in definition when used in the context of different fields of study. As defined in classic philosophy, an axiom is a statement that is so evident or well-established, that it is accepted without controversy or question. As used in modern logic, an axiom is a premise or starting point for reasoning. As used in mathematics, the term ''axiom'' is used in two related but distinguishable senses: "logical axioms" and "non-logical axioms". Logical axioms are usually statements that are taken to be true within the system of logic they define and are often shown in symbolic form (e.g., (''A'' and ''B'') implies ''A''), while non-logical axioms (e.g., ) are actually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to differentiate it from complex hyperbolic spaces, quaternionic hyperbolic spaces and the octononic hyperbolic plane which are the other symmetric spaces of negative curvature. Hyperbolic space serves as the prototype of a Gromov hyperbolic space which is a far-reachin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |