|
Toshikazu Sunada
is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor emeritus of both Meiji University and Tohoku University. He is also distinguished professor of emeritus at Meiji in recognition of achievement over the course of an academic career. Before he joined Meiji University in 2003, he was professor of mathematics at Nagoya University (1988–1991), at the University of Tokyo (1991–1993), and at Tohoku University (1993–2003). Sunada was involved in the creation of the School of Interdisciplinary Mathematical Sciences at Meiji University and is its first dean (2013–2017). Since 2019, he is President of Mathematics Education Society of Japan. Main work Sunada's work covers complex analytic geometry, spectral geometry, dynamical systems, probability, graph theory, discrete geometric analysis, and mathematical crystallography. Among his numerous contributions, the most famous one is a general construction of isosp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tokyo
Tokyo (; ja, 東京, , ), officially the Tokyo Metropolis ( ja, 東京都, label=none, ), is the capital and List of cities in Japan, largest city of Japan. Formerly known as Edo, its metropolitan area () is the most populous in the world, with an estimated 37.468 million residents ; the city proper has a population of 13.99 million people. Located at the head of Tokyo Bay, the prefecture forms part of the Kantō region on the central coast of Honshu, Japan's largest island. Tokyo serves as Economy of Japan, Japan's economic center and is the seat of both the Government of Japan, Japanese government and the Emperor of Japan. Originally a fishing village named Edo, the city became politically prominent in 1603, when it became the seat of the Tokugawa shogunate. By the mid-18th century, Edo was one of the most populous cities in the world with a population of over one million people. Following the Meiji Restoration of 1868, the imperial capital in Kyoto was mov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mark Kac
Mark Kac ( ; Polish: ''Marek Kac''; August 3, 1914 – October 26, 1984) was a Polish American mathematician. His main interest was probability theory. His question, " Can one hear the shape of a drum?" set off research into spectral theory, the idea of understanding the extent to which the spectrum allows one to read back the geometry. (In the end, the answer was "no", in general.) Biography He was born to a Polish-Jewish family; their town, Kremenets ( Polish: "Krzemieniec"), changed hands from the Russian Empire (by then Soviet Ukraine) to Poland after the Peace of Riga, when Kac was a child.Obituary in ''Rochester Democrat & Chronicle'', 11 November 1984 Kac completed his Ph.D. in mathematics at the Polish University o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Albanese Variety
In mathematics, the Albanese variety A(V), named for Giacomo Albanese, is a generalization of the Jacobian variety of a curve. Precise statement The Albanese variety is the abelian variety A generated by a variety V taking a given point of V to the identity of A. In other words, there is a morphism from the variety V to its Albanese variety \operatorname(V), such that any morphism from V to an abelian variety (taking the given point to the identity) factors uniquely through \operatorname(V). For complex manifolds, defined the Albanese variety in a similar way, as a morphism from V to a torus \operatorname(V) such that any morphism to a torus factors uniquely through this map. (It is an analytic variety in this case; it need not be algebraic.) Properties For compact Kähler manifolds the dimension of the Albanese variety is the Hodge number h^, the dimension of the space of differentials of the first kind on V, which for surfaces is called the irregularity of a surface. In terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
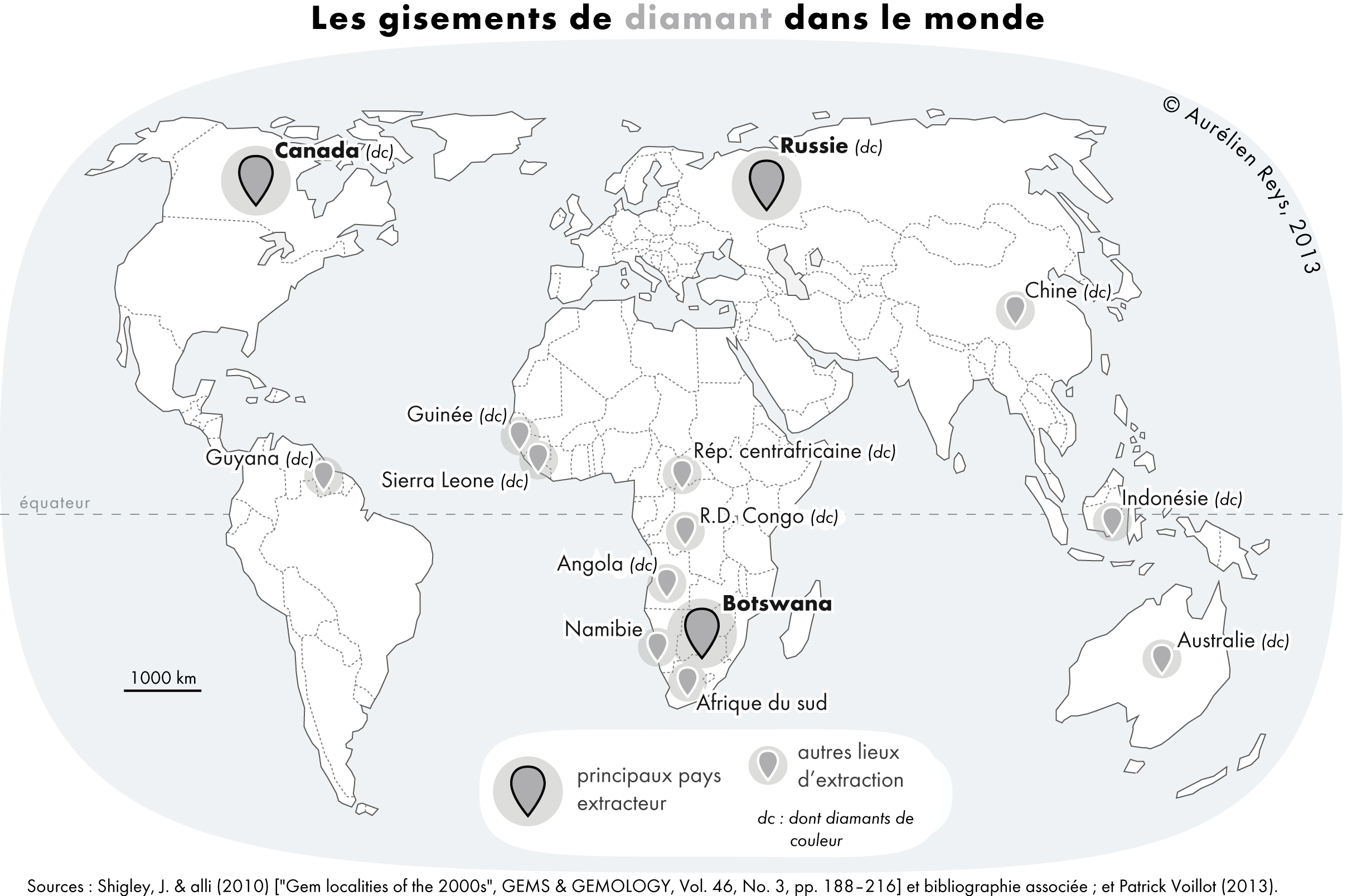
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
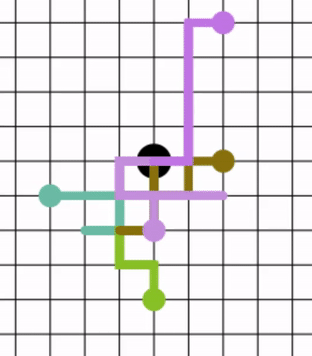
Symmetric Graph
In the mathematical field of graph theory, a graph is symmetric (or arc-transitive) if, given any two pairs of adjacent vertices and of , there is an automorphism :f : V(G) \rightarrow V(G) such that :f(u_1) = u_2 and f(v_1) = v_2. In other words, a graph is symmetric if its automorphism group acts transitively on ordered pairs of adjacent vertices (that is, upon edges considered as having a direction). Such a graph is sometimes also called -transitive or flag-transitive. By definition (ignoring and ), a symmetric graph without isolated vertices must also be vertex-transitive. Since the definition above maps one edge to another, a symmetric graph must also be edge-transitive. However, an edge-transitive graph need not be symmetric, since might map to , but not to . Star graphs are a simple example of being edge-transitive without being vertex-transitive or symmetric. As a further example, semi-symmetric graphs are edge-transitive and regular, but not vertex-transiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge-transitive Graph
In the mathematical field of graph theory, an edge-transitive graph is a graph such that, given any two edges and of , there is an automorphism of that maps to . In other words, a graph is edge-transitive if its automorphism group acts transitively on its edges. Examples and properties The number of connected simple edge-transitive graphs on n vertices is 1, 1, 2, 3, 4, 6, 5, 8, 9, 13, 7, 19, 10, 16, 25, 26, 12, 28 ... Edge-transitive graphs include all symmetric graph, such as the vertices and edges of the cube. Symmetric graphs are also vertex-transitive (if they are connected), but in general edge-transitive graphs need not be vertex-transitive. Every connected edge-transitive graph that is not vertex-transitive must be bipartite, (and hence can be colored with only two colors), and either semi-symmetric or biregular.. Examples of edge but not vertex transitive graphs include the complete bipartite graphs K_ where m ≠ n, which includes the star graphs K_. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laves Graph
In geometry and crystallography, the Laves graph is an infinite and highly symmetric system of points and line segments in three-dimensional Euclidean space, forming a periodic graph. Three equal-length segments meet at 120° angles at each point, and all cycles use ten or more segments. It is the shortest possible triply periodic graph, relative to the volume of its fundamental domain. One arrangement of the Laves graph uses one out of every eight of the points in the integer lattice as its points, and connects all pairs of these points that are nearest neighbors, at distance \sqrt2. It can also be defined, divorced from its geometry, as an abstract undirected graph, a covering graph of the complete graph on four vertices. named this graph after Fritz Laves, who first wrote about it as a crystal structure in 1932. It has also been called the ''K''4 crystal, (10,3)-a network, diamond twin, triamond, and the srs net. The regions of space nearest each vertex of the graph are c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diamond
Diamond is a solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Another solid form of carbon known as graphite is the chemically stable form of carbon at room temperature and pressure, but diamond is metastable and converts to it at a negligible rate under those conditions. Diamond has the highest hardness and thermal conductivity of any natural material, properties that are used in major industrial applications such as cutting and polishing tools. They are also the reason that diamond anvil cells can subject materials to pressures found deep in the Earth. Because the arrangement of atoms in diamond is extremely rigid, few types of impurity can contaminate it (two exceptions are boron and nitrogen). Small numbers of defects or impurities (about one per million of lattice atoms) color diamond blue (boron), yellow (nitrogen), brown (defects), green (radiation exposure), purple, pink, orange, or red. Diamond also has a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Lattice random walk A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ihara Zeta Function
In mathematics, the Ihara zeta function is a zeta function associated with a finite graph. It closely resembles the Selberg zeta function, and is used to relate closed walks to the spectrum of the adjacency matrix. The Ihara zeta function was first defined by Yasutaka Ihara in the 1960s in the context of discrete subgroups of the two-by-two p-adic special linear group. Jean-Pierre Serre suggested in his book ''Trees'' that Ihara's original definition can be reinterpreted graph-theoretically. It was Toshikazu Sunada who put this suggestion into practice in 1985. As observed by Sunada, a regular graph is a Ramanujan graph if and only if its Ihara zeta function satisfies an analogue of the Riemann hypothesis. Definition The Ihara zeta function is defined as the analytic continuation of the infinite product \zeta_\left(u\right)=\prod_\frac The product in the definition is taken over all prime closed geodesics p of the graph G = (V, E), where geodesics which differ by a cyclic ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet's Theorem On Arithmetic Progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers ''a'' and ''d'', there are infinitely many primes of the form ''a'' + ''nd'', where ''n'' is also a positive integer. In other words, there are infinitely many primes that are congruent to ''a'' modulo ''d''. The numbers of the form ''a'' + ''nd'' form an arithmetic progression :a,\ a+d,\ a+2d,\ a+3d,\ \dots,\ and Dirichlet's theorem states that this sequence contains infinitely many prime numbers. The theorem, named after Peter Gustav Lejeune Dirichlet, extends Euclid's theorem that there are infinitely many prime numbers. Stronger forms of Dirichlet's theorem state that for any such arithmetic progression, the sum of the reciprocals of the prime numbers in the progression diverges and that different such arithmetic progressions with the same modulus have approximately the same proportions of primes. Equivalently, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scott A
Scott may refer to: Places Canada * Scott, Quebec, municipality in the Nouvelle-Beauce regional municipality in Quebec * Scott, Saskatchewan, a town in the Rural Municipality of Tramping Lake No. 380 * Rural Municipality of Scott No. 98, Saskatchewan United States * Scott, Arkansas * Scott, Georgia * Scott, Indiana * Scott, Louisiana * Scott, Missouri * Scott, New York * Scott, Ohio * Scott, Wisconsin (other) (several places) * Fort Scott, Kansas * Great Scott Township, St. Louis County, Minnesota * Scott Air Force Base, Illinois * Scott City, Kansas * Scott City, Missouri * Scott County (other) (various states) * Scott Mountain, a mountain in Oregon * Scott River, in California * Scott Township (other) (several places) Elsewhere * 876 Scott, minor planet orbiting the Sun * Scott (crater), a lunar impact crater near the south pole of the Moon * Scott Conservation Park, a protected area in South Australia People * Scott (surname), i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |