|
Tetradecagon
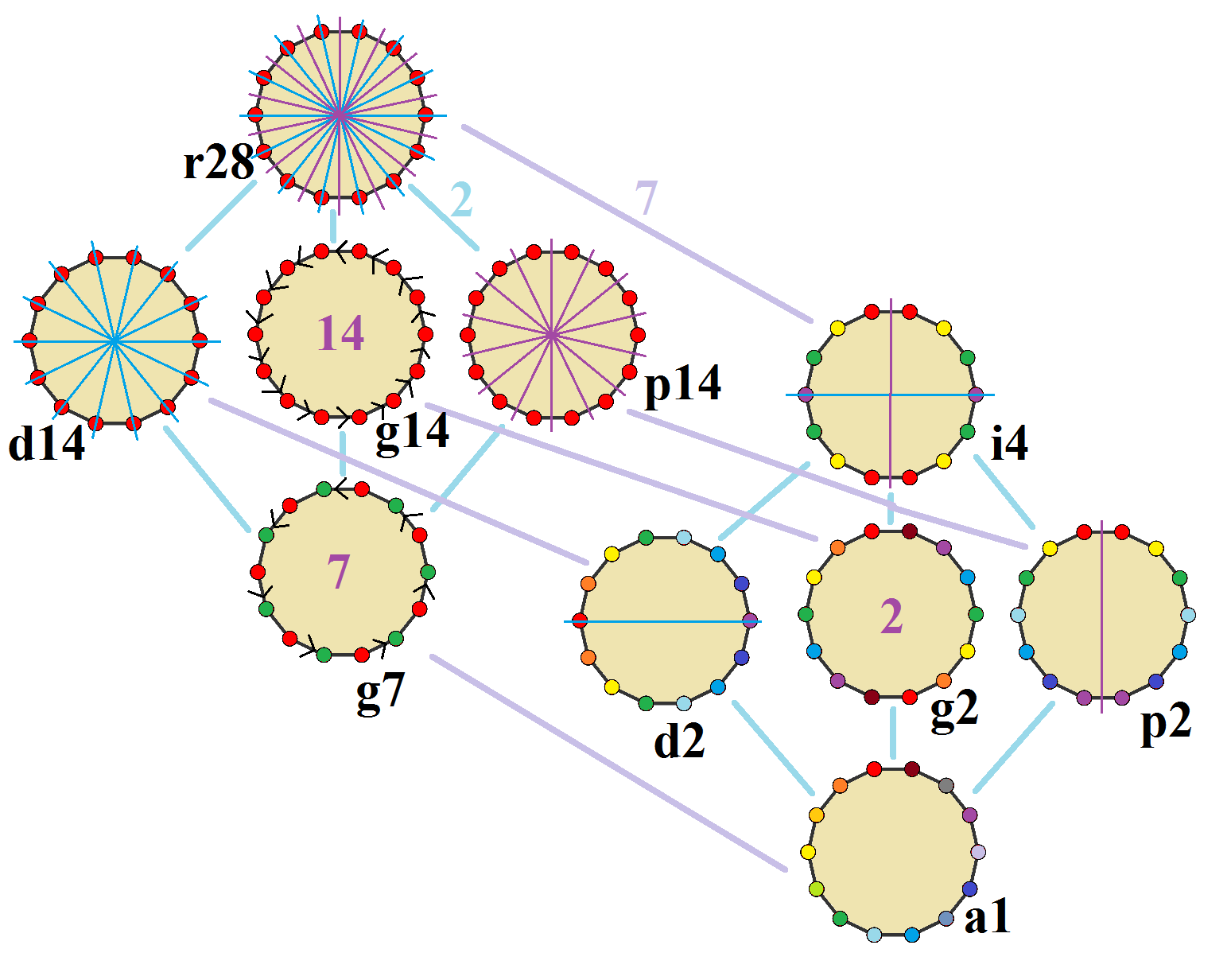
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon. Regular tetradecagon A '' regular tetradecagon'' has Schläfli symbol and can be constructed as a quasiregular truncated heptagon, t, which alternates two types of edges. The area of a regular tetradecagon of side length ''a'' is given by :A = \fraca^2\cot\frac \approx 15.3345a^2 Construction As 14 = 2 × 7, a regular tetradecagon cannot be constructed using a compass and straightedge. However, it is constructible using neusis with use of the angle trisector, or with a marked ruler, as shown in the following two examples. Symmetry The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1. These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14-gon Rhombic Dissection-size2
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon. Regular tetradecagon A ''regular polygon, regular tetradecagon'' has Schläfli symbol and can be constructed as a quasiregular Truncation (geometry), truncated heptagon, t, which alternates two types of edges. The area of a Regular polygon, regular tetradecagon of side length ''a'' is given by :A = \fraca^2\cot\frac \approx 15.3345a^2 Construction As 14 = 2 × 7, a regular tetradecagon cannot be constructible polygon, constructed using a compass and straightedge. However, it is constructible using neusis construction, neusis with use of the angle trisector, or with a marked ruler, as shown in the following two examples. Symmetry The ''regular tetradecagon'' has dihedral symmetry, Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1. These 8 symmetries can be seen in 10 distinct symmetries on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructible Polygon
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinitely many constructible polygons, but only 31 with an odd number of sides are known. Conditions for constructibility Some regular polygons are easy to construct with compass and straightedge; others are not. The ancient Greek mathematicians knew how to construct a regular polygon with 3, 4, or 5 sides, and they knew how to construct a regular polygon with double the number of sides of a given regular polygon.Bold, Benjamin. ''Famous Problems of Geometry and How to Solve Them'', Dover Publications, 1982 (orig. 1969). This led to the question being posed: is it possible to construct ''all'' regular polygons with compass and straightedge? If not, which ''n''-gons (that is, polygons with ''n'' edges) are constructible and which are not? Carl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex polygon, convex, star polygon, star or Skew polygon, skew. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties ''These properties apply to all regular polygons, whether convex or star polygon, star.'' A regular ''n''-sided polygon has rotational symmetry of order ''n''. All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the property of equal-length sides, this implies that every regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotoxal Figure
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged. Isotoxal polygons An isotoxal polygon is an even-sided i.e. equilateral polygon, but not all equilateral polygons are isotoxal. The duals of isotoxal polygons are isogonal polygons. Isotoxal 4n-gons are centrally symmetric, so are also zonogons. In general, an isotoxal 2n-gon has \mathrm_n, (^*nn) dihedral symmetry. For example, a rhombus is an isotoxal "2Ă—2-gon" (quadrilateral) with \mathrm_2, (^*22) symmetry. All regular polygons (equilateral triangle, square, etc.) are isotoxal, having double the minimum symmetry order: a regular n-gon has \mathrm_n, (^*nn) dihedral symmetry. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex polygon, convex, star polygon, star or Skew polygon, skew. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties ''These properties apply to all regular polygons, whether convex or star polygon, star.'' A regular ''n''-sided polygon has rotational symmetry of order ''n''. All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the property of equal-length sides, this implies that every regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isogonal Figure
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces. Technically, one says that for any two vertices there exists a symmetry of the polytope mapping the first isometrically onto the second. Other ways of saying this are that the group of automorphisms of the polytope ''acts transitively'' on its vertices, or that the vertices lie within a single '' symmetry orbit''. All vertices of a finite -dimensional isogonal figure exist on an -sphere. The term isogonal has long been used for polyhedra. Vertex-transitive is a synonym borrowed from modern ideas such as symmetry groups and graph theory. The pseudorhombicuboctahedronwhich is ''not'' isogonaldemonstrates that simply asserting that "all vertices look the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polygon
In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other. Properties Regular polygons are self-dual. The dual of an isogonal (vertex-transitive) polygon is an isotoxal (edge-transitive) polygon. For example, the (isogonal) rectangle and (isotoxal) rhombus are duals. In a cyclic polygon, longer sides correspond to larger exterior angles in the dual (a tangential polygon), and shorter sides to smaller angles. Further, congruent sides in the original polygon yields congruent angles in the dual, and conversely. For example, the dual of a highly acute isosceles triangle is an obtuse isosceles triangle. In the Dorman Luke construction, each face of a dual polyhedron is the dual polygon of the corresponding vertex figure. Duality in quadrilaterals As an example of the side-angle duality of polygons we compare properties of the cyclic and tangential quadrilaterals.Michael de Villiers, ''Some Adventures in Euclid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14-cube T0 A13
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the Îłn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 is called ''the'' unit hypercube. Construction A hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14-cube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the Îłn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 is called ''the'' unit hypercube. Construction A hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaim Goodman-Strauss
Chaim Goodman-Strauss (born June 22, 1967 in Austin TX) is an American mathematician who works in convex geometry, especially aperiodic tiling. He is on the faculty of the University of Arkansas and is a co-author with John H. Conway of ''The Symmetries of Things'', a comprehensive book surveying the mathematical theory of patterns. Education and career Goodman-Strauss received both his B.S. (1988) and Ph.D. (1994) in mathematics from the University of Texas at Austin.Chaim Goodman-Strauss The College Board His doctoral advisor was . He joined the faculty at the |