|
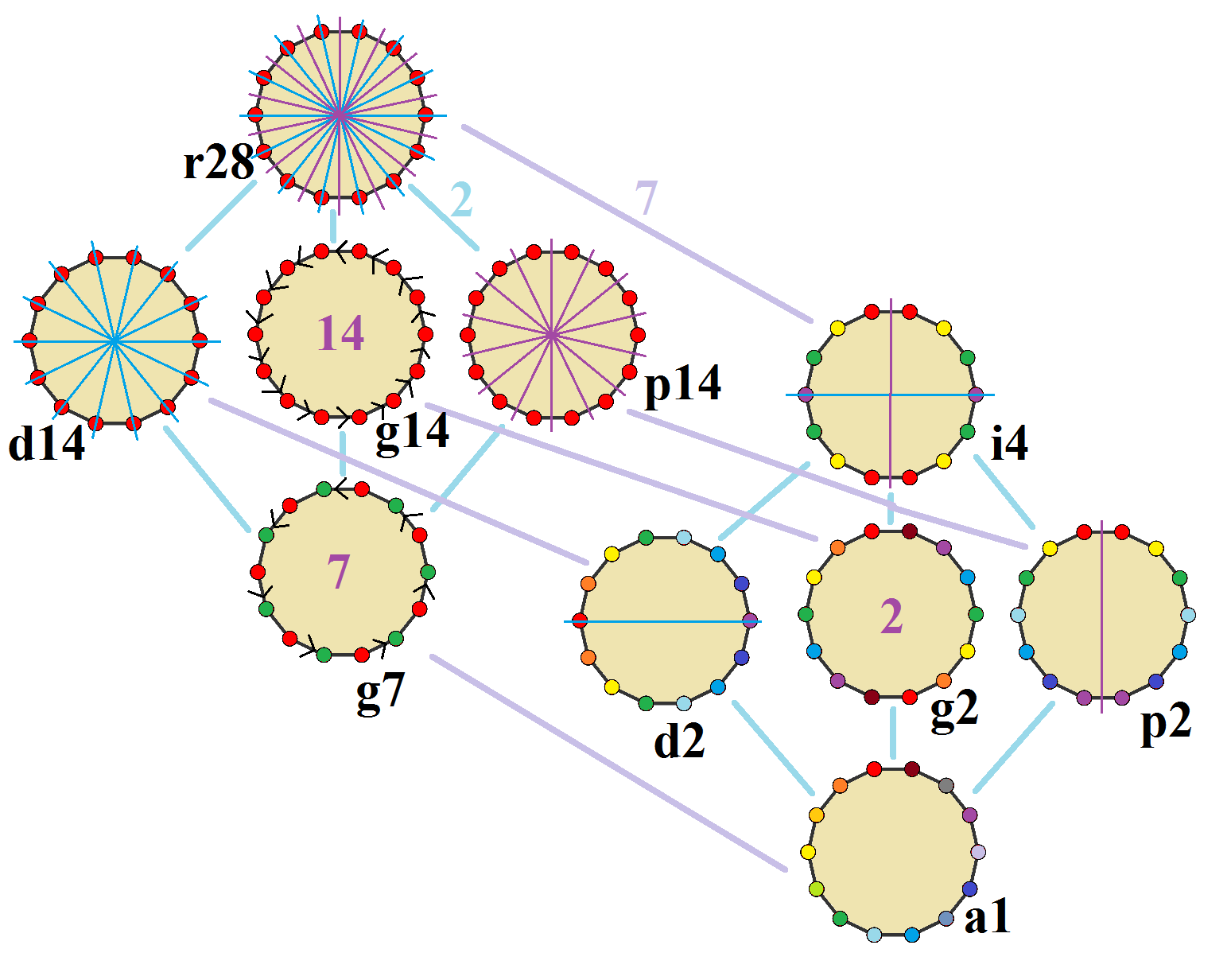
14-gon Rhombic Dissection-size2
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon. Regular tetradecagon A ''regular polygon, regular tetradecagon'' has Schläfli symbol and can be constructed as a quasiregular Truncation (geometry), truncated heptagon, t, which alternates two types of edges. The area of a Regular polygon, regular tetradecagon of side length ''a'' is given by :A = \fraca^2\cot\frac \approx 15.3345a^2 Construction As 14 = 2 × 7, a regular tetradecagon cannot be constructible polygon, constructed using a compass and straightedge. However, it is constructible using neusis construction, neusis with use of the angle trisector, or with a marked ruler, as shown in the following two examples. Symmetry The ''regular tetradecagon'' has dihedral symmetry, Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1. These 8 symmetries can be seen in 10 distinct symmetries on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life. Born and raised in Liverpool, Conway spent the first half of his career at the University of Cambridge before moving to the United States, where he held the John von Neumann Professorship at Princeton University for the rest of his career. On 11 April 2020, at age 82, he died of complications from COVID-19. Early life and education Conway was born on 26 December 1937 in Liverpool, the son of Cyril Horton Conway and Agnes Boyce. He became interested in mathematics at a very early age. By the time he was 11, his ambition was to become a mathematician. After leaving sixth form, he studied mathematics at Gonville and Caius College, Camb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-cube Graph
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces. It can be named by its Schläfli symbol , being composed of 3 6-cubes around each 5-face. It can be called a hepteract, a portmanteau of tesseract (the ''4-cube'') and ''hepta'' for seven (dimensions) in Greek. It can also be called a regular tetradeca-7-tope or tetradecaexon, being a 7 dimensional polytope constructed from 14 regular facets. Related polytopes The ''7-cube'' is 7th in a series of hypercube: The dual of a 7-cube is called a 7-orthoplex, and is a part of the infinite family of cross-polytopes. Applying an '' alternation'' operation, deleting alternating vertices of the hepteract, creates another uniform polytope, called a demihepteract, (part of an infinite family called demihypercubes), which has 14 demihexeractic and 64 6-simplex 6-faces. As a configuration This c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-cube
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces. It can be named by its Schläfli symbol , being composed of 3 6-cubes around each 5-face. It can be called a hepteract, a portmanteau of tesseract (the ''4-cube'') and ''hepta'' for seven (dimensions) in Greek. It can also be called a regular tetradeca-7-tope or tetradecaexon, being a 7 dimensional polytope constructed from 14 regular facets. Related polytopes The ''7-cube'' is 7th in a series of hypercube: The dual of a 7-cube is called a 7-orthoplex, and is a part of the infinite family of cross-polytopes. Applying an '' alternation'' operation, deleting alternating vertices of the hepteract, creates another uniform polytope, called a demihepteract, (part of an infinite family called demihypercubes), which has 14 demihexeractic and 64 6-simplex 6-faces. As a configuration Thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petrie Polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides (but no three) belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie. For every regular polytope there exists an orthogonal projection onto a plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. The plane in question is the Coxeter plane of the symmetry group of the polygon, and the number of sides, , is the Coxeter number of the Coxeter group. These polygons and projected graphs are useful in visualizing symmetric structure of the higher-dimensional regular polytopes. Petrie polygons can be defined more generally for any embedded graph. They form the faces of anothe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zonogon
In geometry, a zonogon is a centrally-symmetric, convex polygon. Equivalently, it is a convex polygon whose sides can be grouped into parallel pairs with equal lengths and opposite orientations. Examples A regular polygon is a zonogon if and only if it has an even number of sides. Thus, the square, regular hexagon, and regular octagon are all zonogons. The four-sided zonogons are the square, the rectangles, the rhombi, and the parallelograms. Tiling and equidissection The four-sided and six-sided zonogons are parallelogons, able to tile the plane by translated copies of themselves, and all convex parallelogons have this form. Every 2n-sided zonogon can be tiled by \tbinom parallelograms. (For equilateral zonogons, a 2n-sided one can be tiled by \tbinom rhombi.) In this tiling, there is parallelogram for each pair of slopes of sides in the 2n-sided zonogon. At least three of the zonogon's vertices must be vertices of only one of the parallelograms in any such tiling. For insta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14-gon Rhombic Dissection-size2
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon. Regular tetradecagon A ''regular polygon, regular tetradecagon'' has Schläfli symbol and can be constructed as a quasiregular Truncation (geometry), truncated heptagon, t, which alternates two types of edges. The area of a Regular polygon, regular tetradecagon of side length ''a'' is given by :A = \fraca^2\cot\frac \approx 15.3345a^2 Construction As 14 = 2 × 7, a regular tetradecagon cannot be constructible polygon, constructed using a compass and straightedge. However, it is constructible using neusis construction, neusis with use of the angle trisector, or with a marked ruler, as shown in the following two examples. Symmetry The ''regular tetradecagon'' has dihedral symmetry, Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1. These 8 symmetries can be seen in 10 distinct symmetries on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14-cube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 is called ''the'' unit hypercube. Construction A hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
14-cube T0 A13
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 is called ''the'' unit hypercube. Construction A hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polygon
In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other. Properties Regular polygons are self-dual. The dual of an isogonal (vertex-transitive) polygon is an isotoxal (edge-transitive) polygon. For example, the (isogonal) rectangle and (isotoxal) rhombus are duals. In a cyclic polygon, longer sides correspond to larger exterior angles in the dual (a tangential polygon), and shorter sides to smaller angles. Further, congruent sides in the original polygon yields congruent angles in the dual, and conversely. For example, the dual of a highly acute isosceles triangle is an obtuse isosceles triangle. In the Dorman Luke construction, each face of a dual polyhedron is the dual polygon of the corresponding vertex figure. Duality in quadrilaterals As an example of the side-angle duality of polygons we compare properties of the cyclic and tangential quadrilaterals.Michael de Villiers, ''Some Adventures in Euclid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotoxal Figure
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged. Isotoxal polygons An isotoxal polygon is an even-sided i.e. equilateral polygon, but not all equilateral polygons are isotoxal. The duals of isotoxal polygons are isogonal polygons. Isotoxal 4n-gons are centrally symmetric, so are also zonogons. In general, an isotoxal 2n-gon has \mathrm_n, (^*nn) dihedral symmetry. For example, a rhombus is an isotoxal "2×2-gon" (quadrilateral) with \mathrm_2, (^*22) symmetry. All regular polygons (equilateral triangle, square, etc.) are isotoxal, having double the minimum symmetry order: a regular n-gon has \mathrm_n, (^*nn) dihedral symmetry. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |