14-gon Rhombic Dissection-size2 on:
[Wikipedia]
[Google]
[Amazon]
In
/ref> as shown in the following two examples.
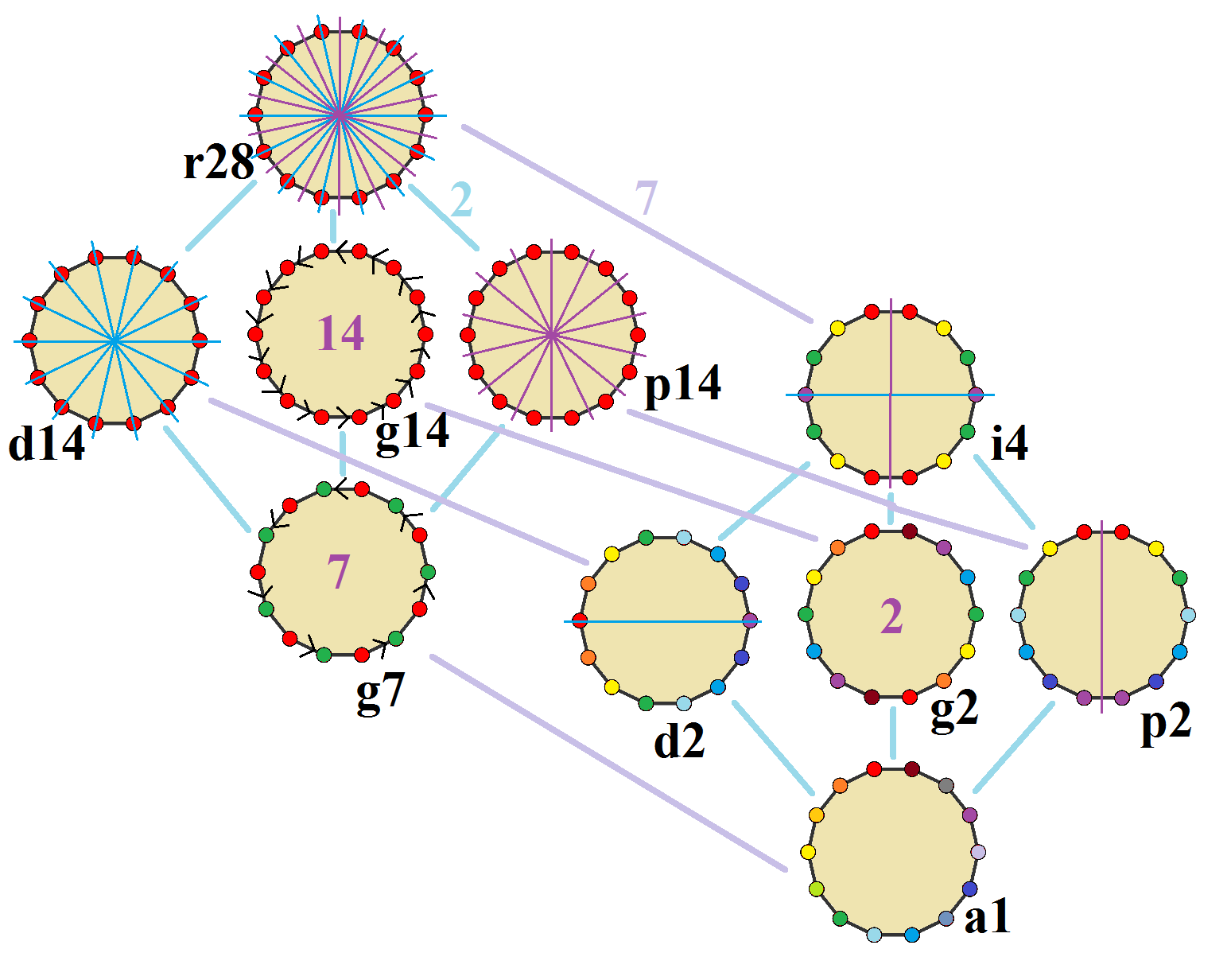 The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4
The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4
 A tetradecagram is a 14-sided star polygon, represented by symbol . There are two regular
A tetradecagram is a 14-sided star polygon, represented by symbol . There are two regular
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...
.
Regular tetradecagon
A ''regular
The term regular can mean normal or in accordance with rules. It may refer to:
People
* Moses Regular (born 1971), America football player
Arts, entertainment, and media Music
* "Regular" (Badfinger song)
* Regular tunings of stringed instrum ...
tetradecagon'' has Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to mor ...
and can be constructed as a quasiregular truncated
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones.
Truncation may also refer to:
Mathematics
* Truncation (statistics) refers to measurements which have been cut of ...
heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of '' septua-'', a Latin-derived numerical prefix, rather than '' hepta-'', a Greek-derived n ...
, t, which alternates two types of edges.
The area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while ''surface area'' refers to the area of an open su ...
of a regular
The term regular can mean normal or in accordance with rules. It may refer to:
People
* Moses Regular (born 1971), America football player
Arts, entertainment, and media Music
* "Regular" (Badfinger song)
* Regular tunings of stringed instrum ...
tetradecagon of side length ''a'' is given by
:
Construction
As 14 = 2 × 7, a regular tetradecagon cannot be constructed using acompass and straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
. However, it is constructible using neusis
In geometry, the neusis (; ; plural: grc, νεύσεις, neuseis, label=none) is a geometric construction method that was used in antiquity by Greek mathematicians.
Geometric construction
The neusis construction consists of fitting a line e ...
with use of the angle trisector
Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge a ...
, or with a marked ruler,Weisstein, Eric W. "Heptagon." From MathWorld, A Wolfram Web Resource./ref> as shown in the following two examples.

Symmetry
 The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4
The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group
In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted C''n'', that is generated by a single element. That is, it is a set of invertible elements with a single associative bi ...
symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches ...
labels these by a letter and group order. Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can seen as directed edge
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs.
Definition
In formal terms, a directed graph is an ordered pai ...
s.
The highest symmetry irregular tetradecagons are d14, an isogonal tetradecagon constructed by seven mirrors which can alternate long and short edges, and p14, an isotoxal
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two e ...
tetradecagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals
''Duals'' is a compilation album by the Irish rock band U2. It was released in April 2011 to u2.com subscribers.
Track listing
:* "Where the Streets Have No Name" and "Amazing Grace" are studio mix of U2's performance at the Rose Bowl, ...
of each other and have half the symmetry order of the regular tetradecagon.
Dissection
Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
states that every zonogon
In geometry, a zonogon is a central symmetry, centrally-symmetric, convex polygon. Equivalently, it is a convex polygon whose sides can be grouped into Parallel (geometry), parallel pairs with equal lengths and opposite orientations.
Examples
...
(a 2''m''-gon whose opposite sides are parallel and of equal length) can be dissected into ''m''(''m''-1)/2 parallelograms.
In particular this is true for regular polygon
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be either convex, star or skew. In the limit, a sequence ...
s with evenly many sides, in which case the parallelograms are all rhombi. For the ''regular tetradecagon'', ''m''=7, and it can be divided into 21: 3 sets of 7 rhombs. This decomposition is based on a Petrie polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a ...
projection of a 7-cube
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces.
It can be named by its Schläfli symbol , being ...
, with 21 of 672 faces. The list defines the number of solutions as 24698, including up to 14-fold rotations and chiral forms in reflection.
Numismatic use
The regular tetradecagon is used as the shape of some commemorative gold and silverMalaysia
Malaysia ( ; ) is a country in Southeast Asia. The federation, federal constitutional monarchy consists of States and federal territories of Malaysia, thirteen states and three federal territories, separated by the South China Sea into two r ...
n coins, the number of sides representing the 14 states of the Malaysian Federation.
Related figures
star polygon
In geometry, a star polygon is a type of non- convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operation ...
s: and , using the same vertices, but connecting every third or fifth points. There are also three compounds: is reduced to 2 as two heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of '' septua-'', a Latin-derived numerical prefix, rather than '' hepta-'', a Greek-derived n ...
s, while and are reduced to 2 and 2 as two different heptagram
A heptagram, septagram, septegram or septogram is a seven-point star drawn with seven straight strokes.
The name ''heptagram'' combines a numeral prefix, '' hepta-'', with the Greek suffix ''-gram''. The ''-gram'' suffix derives from ''γρ� ...
s, and finally is reduced to seven digon
In geometry, a digon is a polygon with two sides ( edges) and two vertices. Its construction is degenerate in a Euclidean plane because either the two sides would coincide or one or both would have to be curved; however, it can be easily visu ...
s.
A notable application of a fourteen-pointed star is in the flag of Malaysia
The national flag of Malaysia, also known as the Stripes of Glory ( ms, Jalur Gemilang), is composed of a field of 14 alternating red and white stripes along the fly and a blue canton bearing a crescent and a 14-point star known as the ''Bint ...
, which incorporates a yellow tetradecagram in the top-right corner, representing the unity of the thirteen states
State may refer to:
Arts, entertainment, and media Literature
* '' State Magazine'', a monthly magazine published by the U.S. Department of State
* ''The State'' (newspaper), a daily newspaper in Columbia, South Carolina, United States
* ''Our ...
with the federal government
A federation (also known as a federal state) is a political entity characterized by a union of partially self-governing provinces, states, or other regions under a central federal government (federalism). In a federation, the self-govern ...
.
Deeper truncations of the regular heptagon and heptagram
A heptagram, septagram, septegram or septogram is a seven-point star drawn with seven straight strokes.
The name ''heptagram'' combines a numeral prefix, '' hepta-'', with the Greek suffix ''-gram''. The ''-gram'' suffix derives from ''γρ� ...
s can produce isogonal (vertex-transitive
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of fa ...
) intermediate tetradecagram forms with equally spaced vertices and two edge lengths. Other truncations can form double covering polygons 2, namely: t2, t2, and t2.The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), ''Metamorphoses of polygons'', Branko Grünbaum
Branko Grünbaum ( he, ברנקו גרונבאום; 2 October 1929 – 14 September 2018) was a Croatian-born mathematician of Jewish descentisotoxal polygon
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two e ...
can be labeled as with outer most internal angle α, and a star polygon , with ''q'' is a winding number
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of tu ...
, and gcd(''p'',''q'')=1, ''q''<''p''. Isotoxal tetradecagons have ''p''=7, and since 7 is prime all solutions, q=1..6, are polygons.
Petrie polygons
Regular skew tetradecagons exist asPetrie polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a ...
for many higher-dimensional polytopes, shown in these skew orthogonal projection
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if i ...
s, including:
References
External links
* {{Polygons Polygons by the number of sides