|
Test Statistic
A test statistic is a statistic (a quantity derived from the sample) used in statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistic
A statistic (singular) or sample statistic is any quantity computed from values in a sample which is considered for a statistical purpose. Statistical purposes include estimating a population parameter, describing a sample, or evaluating a hypothesis. The average (or mean) of sample values is a statistic. The term statistic is used both for the function and for the value of the function on a given sample. When a statistic is being used for a specific purpose, it may be referred to by a name indicating its purpose. When a statistic is used for estimating a population parameter, the statistic is called an ''estimator''. A population parameter is any characteristic of a population under study, but when it is not feasible to directly measure the value of a population parameter, statistical methods are used to infer the likely value of the parameter on the basis of a statistic computed from a sample taken from the population. For example, the sample mean is an unbiased estimator of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-test
A ''t''-test is any statistical hypothesis test in which the test statistic follows a Student's ''t''-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a Scale parameter, scaling term in the test statistic were known (typically, the scaling term is unknown and therefore a nuisance parameter). When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student's ''t'' distribution. The ''t''-test's most common application is to test whether the means of two populations are different. History The term "''t''-statistic" is abbreviated from "hypothesis test statistic". In statistics, the t-distribution was first derived as a Posterior probability, posterior distribution in 1876 by Friedrich Robert Helmert, Helmert and Jacob Lüroth, Lüroth. The t-distribution also appeared in a more general form as Pearson Type Pearson distribution, IV di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Likelihood-ratio Test
In statistics, the likelihood-ratio test assesses the goodness of fit of two competing statistical models based on the ratio of their likelihoods, specifically one found by maximization over the entire parameter space and another found after imposing some constraint. If the constraint (i.e., the null hypothesis) is supported by the observed data, the two likelihoods should not differ by more than sampling error. Thus the likelihood-ratio test tests whether this ratio is significantly different from one, or equivalently whether its natural logarithm is significantly different from zero. The likelihood-ratio test, also known as Wilks test, is the oldest of the three classical approaches to hypothesis testing, together with the Lagrange multiplier test and the Wald test. In fact, the latter two can be conceptualized as approximations to the likelihood-ratio test, and are asymptotically equivalent. In the case of comparing two models each of which has no unknown parameters, use o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Distribution
In statistical hypothesis testing, the null distribution is the probability distribution of the test statistic when the null hypothesis is true. For example, in an F-test, the null distribution is an F-distribution. Null distribution is a tool scientists often use when conducting experiments. The null distribution is the distribution of two sets of data under a null hypothesis. If the results of the two sets of data are not outside the parameters of the expected results, then the null hypothesis is said to be true. Examples of application The null hypothesis is often a part of an experiment. The null hypothesis tries to show that among two sets of data, there is no statistical difference between the results of doing one thing as opposed to doing a different thing. For an example of this, a scientist might be trying to prove that people who walk two miles a day have healthier hearts than people who walk less than two miles a day. The scientist would use the null hypothesis to test ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
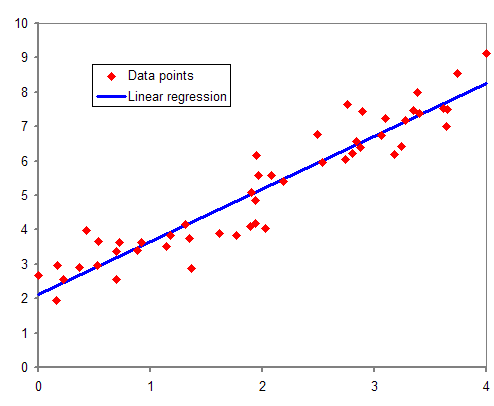
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
McGraw Hill
McGraw Hill is an American educational publishing company and one of the "big three" educational publishers that publishes educational content, software, and services for pre-K through postgraduate education. The company also publishes reference and trade publications for the medical, business, and engineering professions. McGraw Hill operates in 28 countries, has about 4,000 employees globally, and offers products and services to about 140 countries in about 60 languages. Formerly a division of The McGraw Hill Companies (later renamed McGraw Hill Financial, now S&P Global), McGraw Hill Education was divested and acquired by Apollo Global Management in March 2013 for $2.4 billion in cash. McGraw Hill was sold in 2021 to Platinum Equity for $4.5 billion. Corporate History McGraw Hill was founded in 1888 when James H. McGraw, co-founder of the company, purchased the ''American Journal of Railway Appliances''. He continued to add further publications, eventually establishing The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Distribution
In probability theory and statistics, the binomial distribution with parameters ''n'' and ''p'' is the discrete probability distribution of the number of successes in a sequence of ''n'' independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: ''success'' (with probability ''p'') or ''failure'' (with probability q=1-p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., ''n'' = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance. The binomial distribution is frequently used to model the number of successes in a sample of size ''n'' drawn with replacement from a population of size ''N''. If the sampling is carried out without replacement, the draws are not independent and so the resulting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Welch's T Test
In statistics, Welch's ''t''-test, or unequal variances ''t''-test, is a two-sample location test which is used to test the hypothesis that two populations have equal means. It is named for its creator, Bernard Lewis Welch, is an adaptation of Student's ''t''-test, and is more reliable when the two samples have unequal variances and possibly unequal sample sizes. These tests are often referred to as "unpaired" or "independent samples" ''t''-tests, as they are typically applied when the statistical units underlying the two samples being compared are non-overlapping. Given that Welch's ''t''-test has been less popular than Student's ''t''-test and may be less familiar to readers, a more informative name is "Welch's unequal variances ''t''-test" — or "unequal variances ''t''-test" for brevity. Assumptions Student's ''t''-test assumes that the sample means being compared for two populations are normally distributed, and that the populations have equal variances. Welch's ''t''-tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev's Inequality
In probability theory, Chebyshev's inequality (also called the Bienaymé–Chebyshev inequality) guarantees that, for a wide class of probability distributions, no more than a certain fraction of values can be more than a certain distance from the mean. Specifically, no more than 1/''k''2 of the distribution's values can be ''k'' or more standard deviations away from the mean (or equivalently, at least 1 − 1/''k''2 of the distribution's values are less than ''k'' standard deviations away from the mean). The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers. Its practical usage is similar to the 68–95–99.7 rule, which applies only to normal distributions. Chebyshev's inequality is more general, stating th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Error
The standard error (SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM). The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean. Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z-test
A ''Z''-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Z-tests test the mean of a distribution. For each significance level in the confidence interval, the ''Z''-test has a single critical value (for example, 1.96 for 5% two tailed) which makes it more convenient than the Student's ''t''-test whose critical values are defined by the sample size (through the corresponding degrees of freedom). Both the Z test and Student's t-test have similarities in that they both help determine the significance of a set of data. However, the z-test is rarely used in practice because the population deviation is difficult to determine. Applicability Because of the central limit theorem, many test statistics are approximately normally distributed for large samples. Therefore, many statistical tests can be conveniently performed as approximate ''Z''-tests if the sample size is large or the populat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
:Category:Statistical Tests
{{CatAutoTOC ...
Statistical hypothesis testing Tests Test(s), testing, or TEST may refer to: * Test (assessment), an educational assessment intended to measure the respondents' knowledge or other abilities Arts and entertainment * ''Test'' (2013 film), an American film * ''Test'' (2014 film), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |