|
Tensor Rank Decomposition
In multilinear algebra, the tensor rank decomposition or rank-''R'' decomposition is the decomposition of a tensor as a sum of ''R'' rank-1 tensors, where ''R'' is minimal. Computing this decomposition is an open problem. Canonical polyadic decomposition (CPD) is a variant of the tensor rank decomposition, in which the tensor is approximated as a sum of ''K'' rank-1 tensors for a user-specified ''K''. The CP decomposition has found some applications in linguistics and chemometrics. It was introduced by Frank Lauren Hitchcock in 1927 and later rediscovered several times, notably in psychometrics. The CP decomposition is referred to as CANDECOMP, PARAFAC, or CANDECOMP/PARAFAC (CP). Note that the PARAFAC2 rank decomposition is a variation of the CP decomposition. Another popular generalization of the matrix SVD known as the higher-order singular value decomposition computes orthonormal mode matrices and has found applications in econometrics, signal processing, computer vision, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Multilinear Algebra
Multilinear algebra is the study of Function (mathematics), functions with multiple vector space, vector-valued Argument of a function, arguments, with the functions being Linear map, linear maps with respect to each argument. It involves concepts such as Matrix (mathematics), matrices, tensors, multivectors, System of linear equations, systems of linear equations, Higher-dimensional space, higher-dimensional spaces, Determinant, determinants, inner product, inner and outer product, outer products, and Dual space, dual spaces. It is a mathematical tool used in engineering, machine learning, physics, and mathematics. Origin While many theoretical concepts and applications involve Vector space, single vectors, mathematicians such as Hermann Grassmann considered structures involving pairs, triplets, and multivectors that generalize Vector (mathematics and physics), vectors. With multiple combinational possibilities, the space of multivectors expands to 2''n'' dimensions, where ''n'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Field Extension
In mathematics, particularly in algebra, a field extension is a pair of fields K \subseteq L, such that the operations of ''K'' are those of ''L'' restricted to ''K''. In this case, ''L'' is an extension field of ''K'' and ''K'' is a subfield of ''L''. For example, under the usual notions of addition and multiplication, the complex numbers are an extension field of the real numbers; the real numbers are a subfield of the complex numbers. Field extensions are fundamental in algebraic number theory, and in the study of polynomial roots through Galois theory, and are widely used in algebraic geometry. Subfield A subfield K of a field L is a subset K\subseteq L that is a field with respect to the field operations inherited from L. Equivalently, a subfield is a subset that contains the multiplicative identity 1, and is closed under the operations of addition, subtraction, multiplication, and taking the inverse of a nonzero element of K. As , the latter definition implies K and L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer-assisted Proof
Automation describes a wide range of technologies that reduce human intervention in processes, mainly by predetermining decision criteria, subprocess relationships, and related actions, as well as embodying those predeterminations in machines. Automation has been achieved by various means including mechanical, hydraulic, pneumatic, electrical, electronic devices, and computers, usually in combination. Complicated systems, such as modern factories, airplanes, and ships typically use combinations of all of these techniques. The benefit of automation includes labor savings, reducing waste, savings in electricity costs, savings in material costs, and improvements to quality, accuracy, and precision. Automation includes the use of various equipment and control systems such as machinery, processes in factories, boilers, and heat-treating ovens, switching on telephone networks, steering, stabilization of ships, aircraft and other applications and vehicles with reduced human ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
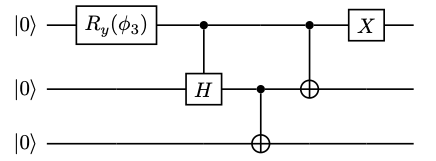
W State
The W state is an quantum entanglement, entangled quantum state of three qubits which in the bra-ket notation has the following shape : , \mathrm\rangle = \frac(, 001\rangle + , 010\rangle + , 100\rangle) and which is remarkable for representing a specific type of multipartite entanglement and for occurring in several applications in quantum information theory. Particles prepared in this state reproduce the properties of Bell's theorem, which states that no classical theory of local hidden variables can produce the predictions of quantum mechanics. The state is named after Wolfgang Dür, Wolfgang Dür, who first reported the state together with Guifré Vidal, and Juan Ignacio Cirac Sasturain, Ignacio Cirac in 2000. Properties The W state is the representative of one of the two non-biseparable classes of three-qubit states, the other being the Greenberger–Horne–Zeilinger state, , \mathrm\rangle = (, 000\rangle + , 111\rangle)/\sqrt. The , \mathrm\rangle and , \mathrm\rangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
SIAM Journal On Scientific Computing
The ''SIAM Journal on Scientific Computing'' (''SISC''), formerly ''SIAM Journal on Scientific & Statistical Computing'', is a scientific journal focusing on the research articles on numerical methods and techniques for scientific computation. It is published by the Society for Industrial and Applied Mathematics (SIAM). Hans De Sterck is the current editor-in-chief, assuming the role in January 2022. The impact factor is currently around 2. This journal papers address computational issues relevant to solution of scientific or engineering problems and include computational results demonstrating the effectiveness of proposed techniques. They are classified into three categories: 1) Methods and Algorithms for Scientific Computing. 2) Computational Methods in Science and Engineering. 3) Software and High-Performance Computing. The first type papers focus on theoretical analysis, provided that relevance to applications in science and engineering is demonstrated. They are supposed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matrix Multiplication Algorithm
Because matrix multiplication is such a central operation in many numerical algorithms, much work has been invested in making matrix multiplication algorithms efficient. Applications of matrix multiplication in computational problems are found in many fields including scientific computing and pattern recognition and in seemingly unrelated problems such as counting the paths through a Graph (graph theory), graph. Many different algorithms have been designed for multiplying matrices on different types of hardware, including parallel computing, parallel and distributed computing, distributed systems, where the computational work is spread over multiple processors (perhaps over a network). Directly applying the mathematical definition of matrix multiplication gives an algorithm that Analysis of algorithms, takes time on the order of Field (mathematics), field operations to multiply two matrices over that field ( in big O notation). Better asymptotic bounds on the time required to mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
SIAM Journal On Matrix Analysis And Applications
The ''SIAM Journal on Matrix Analysis and Applications'' is a peer-reviewed scientific journal covering matrix analysis and its applications. The relevant applications include signal processing, systems and control theory, statistics, Markov chains, mathematical biology, graph theory, and data science. The journal was originally established as the ''SIAM Journal on Algebraic and Discrete Methods'' in 1980, until it split into '' SIAM Journal on Discrete Mathematics'' and the current title in 1988. The journal is published by the Society for Industrial and Applied Mathematics. The founding editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The editor-in-chief heads all departments of the organization and is held accoun ... was Gene H. Golub, who established the journal in 1980. The current editor is Michele Benzi ( Scuola Normale Superiore). Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematische Annalen
''Mathematische Annalen'' (abbreviated as ''Math. Ann.'' or, formerly, ''Math. Annal.'') is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann. Subsequent managing editors were Felix Klein, David Hilbert, Otto Blumenthal, Erich Hecke, Heinrich Behnke, Hans Grauert, Heinz Bauer, Herbert Amann, Jean-Pierre Bourguignon, Wolfgang Lück, Nigel Hitchin, and Thomas Schick. Currently, the managing editor of Mathematische Annalen is Yoshikazu Giga (University of Tokyo). Volumes 1–80 (1869–1919) were published by Teubner. Since 1920 (vol. 81), the journal has been published by Springer. In the late 1920s, under the editorship of Hilbert, the journal became embroiled in controversy over the participation of L. E. J. Brouwer on its editorial board, a spillover from the foundational Brouwer–Hilbert controversy. Between 1945 and 1947, the journal briefly ceased publication. References External links''Mathematische Annalen''homepage a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transactions Of The American Mathematical Society
The ''Transactions of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of pure and applied mathematics published by the American Mathematical Society. It was established in 1900. As a requirement, all articles must be more than 15 printed pages. Its ISSN number is 0002-9947. See also * ''Bulletin of the American Mathematical Society'' * ''Journal of the American Mathematical Society'' * '' Memoirs of the American Mathematical Society'' * '' Notices of the American Mathematical Society'' * ''Proceedings of the American Mathematical Society'' References External links * ''Transactions of the American Mathematical Society''on JSTOR JSTOR ( ; short for ''Journal Storage'') is a digital library of academic journals, books, and primary sources founded in 1994. Originally containing digitized back issues of academic journals, it now encompasses books and other primary source ... American Mathematical Society academic journals Mathematics jo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Almost Everywhere
In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to the concept of measure zero, and is analogous to the notion of '' almost surely'' in probability theory. More specifically, a property holds almost everywhere if it holds for all elements in a set except a subset of measure zero, or equivalently, if the set of elements for which the property holds is conull. In cases where the measure is not complete, it is sufficient that the set be contained within a set of measure zero. When discussing sets of real numbers, the Lebesgue measure is usually assumed unless otherwise stated. The term ''almost everywhere'' is abbreviated ''a.e.''; in older literature ''p.p.'' is used, to stand for the equivalent French language phrase ''presque partout''. A set with full measure is one whose complement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Algebra And Its Applications
''Linear Algebra and its Applications'' is a biweekly peer-reviewed mathematics journal published by Elsevier and covering matrix theory and finite-dimensional linear algebra. History The journal was established in January 1968 with A.J. Hoffman, A.S. Householder, A.M. Ostrowski, H. Schneider, and O. Taussky Todd as founding editors-in-chief. The current editors-in-chief are Richard A. Brualdi ( University of Wisconsin at Madison), Volker Mehrmann (Technische Universität Berlin), and Peter Semrl (University of Ljubljana). Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 1.401. References {{Reflist Algebra journ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Volker Strassen
Volker Strassen (born April 29, 1936) is a German mathematician, a professor emeritus in the department of mathematics and statistics at the University of Konstanz. For important contributions to the analysis of algorithms he has received many awards, including the Cantor medal, the Konrad Zuse Medal, the Paris Kanellakis Award for work on randomized primality testing, the Knuth Prize for "seminal and influential contributions to the design and analysis of efficient algorithms." Biography Strassen was born on April 29, 1936, in Düsseldorf-Gerresheim.. After studying music, philosophy, physics, and mathematics at several German universities, he received his Ph.D. in mathematics in 1962 from the University of Göttingen under the supervision of . He then took a position in the department of statistics at the University of California, Berkeley while performing his habilitation at the University of Erlangen-Nuremberg, where Jacobs had since moved. In 1968, Strassen moved to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |