|
Tree (set Theory)
In botany, a tree is a perennial plant with an elongated stem, or trunk, usually supporting branches and leaves. In some usages, the definition of a tree may be narrower, e.g., including only woody plants with secondary growth, only plants that are usable as lumber, or only plants above a specified height. But wider definitions include taller palms, tree ferns, bananas, and bamboos. Trees are not a monophyletic taxonomic group but consist of a wide variety of plant species that have independently evolved a trunk and branches as a way to tower above other plants to compete for sunlight. The majority of tree species are angiosperms or hardwoods; of the rest, many are gymnosperms or softwoods. Trees tend to be long-lived, some trees reaching several thousand years old. Trees evolved around 400 million years ago, and it is estimated that there are around three trillion mature trees in the world currently. A tree typically has many secondary branches supported clear of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ash Tree - Geograph
Ash is the solid remnants of fires. Specifically, ''ash'' refers to all non-aqueous, non-gaseous residues that remain after something combustion, burns. In analytical chemistry, to analyse the mineral and metal content of chemical samples, ash (analytical chemistry), ash is the non-gaseous, non-liquid residue after complete combustion. Ashes as the end product of incomplete combustion are mostly mineral, but usually still contain an amount of combustible organic compound, organic or other Redox, oxidizable residues. The best-known type of ash is wood ash, as a product of wood combustion in campfires, fireplaces, etc. The darker the wood ashes, the higher the content of remaining charcoal from incomplete combustion. The ashes are of different types. Some ashes contain natural compounds that make soil Soil fertility, fertile. Others have chemical compounds that can be toxic but may break up in soil from chemical changes and microorganism activity. Like soap, ash is also a disin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergent Evolution
Convergent evolution is the independent evolution of similar features in species of different periods or epochs in time. Convergent evolution creates analogous structures that have similar form or function but were not present in the last common ancestor of those groups. The cladistic term for the same phenomenon is Cladogram#Homoplasies, homoplasy. The recurrent evolution of flight is a classic example, as flying pterygota, insects, birds, pterosaurs, and bats have independently evolved the useful capacity of flight. Functionally similar features that have arisen through convergent evolution are ''analogous'', whereas ''homology (biology), homologous'' structures or traits have a common origin but can have dissimilar functions. Bird, bat, and pterosaur wings are analogous structures, but their forelimbs are homologous, sharing an ancestral state despite serving different functions. The opposite of convergence is divergent evolution, where related species evolve different trai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmosphere Of Earth
The atmosphere of Earth is composed of a layer of gas mixture that surrounds the Earth's planetary surface (both lands and oceans), known collectively as air, with variable quantities of suspended aerosols and particulates (which create weather features such as clouds and hazes), all retained by gravity of Earth, Earth's gravity. The atmosphere serves as a protective buffer between the Earth's surface and outer space, shields the surface from most meteoroids and ultraviolet solar irradiance, solar radiation, keeps it warm and reduces diurnal temperature variation (temperature extremes between daytime, day and night) through heat retention (greenhouse effect), redistributes heat and moisture among different regions via air currents, and provides the atmospheric chemistry, chemical and climate conditions allowing life to exist and evolution, evolve on Earth. By mole fraction (i.e., by quantity of molecules), dry air contains 78.08% nitrogen, 20.95% oxygen, 0.93% argon, 0.04% carbon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carbon Dioxide
Carbon dioxide is a chemical compound with the chemical formula . It is made up of molecules that each have one carbon atom covalent bond, covalently double bonded to two oxygen atoms. It is found in a gas state at room temperature and at normally-encountered concentrations it is odorless. As the source of carbon in the carbon cycle, atmospheric is the primary carbon source for life on Earth. In the air, carbon dioxide is transparent to visible light but absorbs infrared, infrared radiation, acting as a greenhouse gas. Carbon dioxide is soluble in water and is found in groundwater, lakes, ice caps, and seawater. It is a trace gas Carbon dioxide in Earth's atmosphere, in Earth's atmosphere at 421 parts per million (ppm), or about 0.042% (as of May 2022) having risen from pre-industrial levels of 280 ppm or about 0.028%. Burning fossil fuels is the main cause of these increased concentrations, which are the primary cause of climate change.IPCC (2022Summary for pol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Climate
Climate is the long-term weather pattern in a region, typically averaged over 30 years. More rigorously, it is the mean and variability of meteorological variables over a time spanning from months to millions of years. Some of the meteorological variables that are commonly measured are temperature, humidity, atmospheric pressure, wind, and precipitation. In a broader sense, climate is the state of the components of the climate system, including the atmosphere, hydrosphere, cryosphere, lithosphere and biosphere and the interactions between them. The climate of a location is affected by its latitude, longitude, terrain, altitude, land use and nearby water bodies and their currents. Climates can be classified according to the average and typical variables, most commonly temperature and precipitation. The most widely used classification scheme is the Köppen climate classification. The Thornthwaite system, in use since 1948, incorporates evapotranspiration along ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soil Erosion
Soil erosion is the denudation or wearing away of the Topsoil, upper layer of soil. It is a form of soil degradation. This natural process is caused by the dynamic activity of erosive agents, that is, water, ice (glaciers), snow, Atmosphere of Earth, air (wind), plants, and animals (including humans). In accordance with these agents, erosion is sometimes divided into water erosion, glacial erosion, snow erosion, Aeolian erosion, wind (aeolian) erosion, Zoogenic erosion, zoogenic erosion and anthropogenic erosion such as tillage erosion. Soil erosion may be a slow process that continues relatively unnoticed, or it may occur at an alarming rate causing a serious loss of topsoil. The loss of soil from Agricultural land, farmland may be reflected in reduced crop production potential, lower surface water quality and damaged drainage networks. Soil erosion could also cause sinkholes. Human activities have increased by 10–50 times the rate at which erosion is occurring world-wide. Exc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
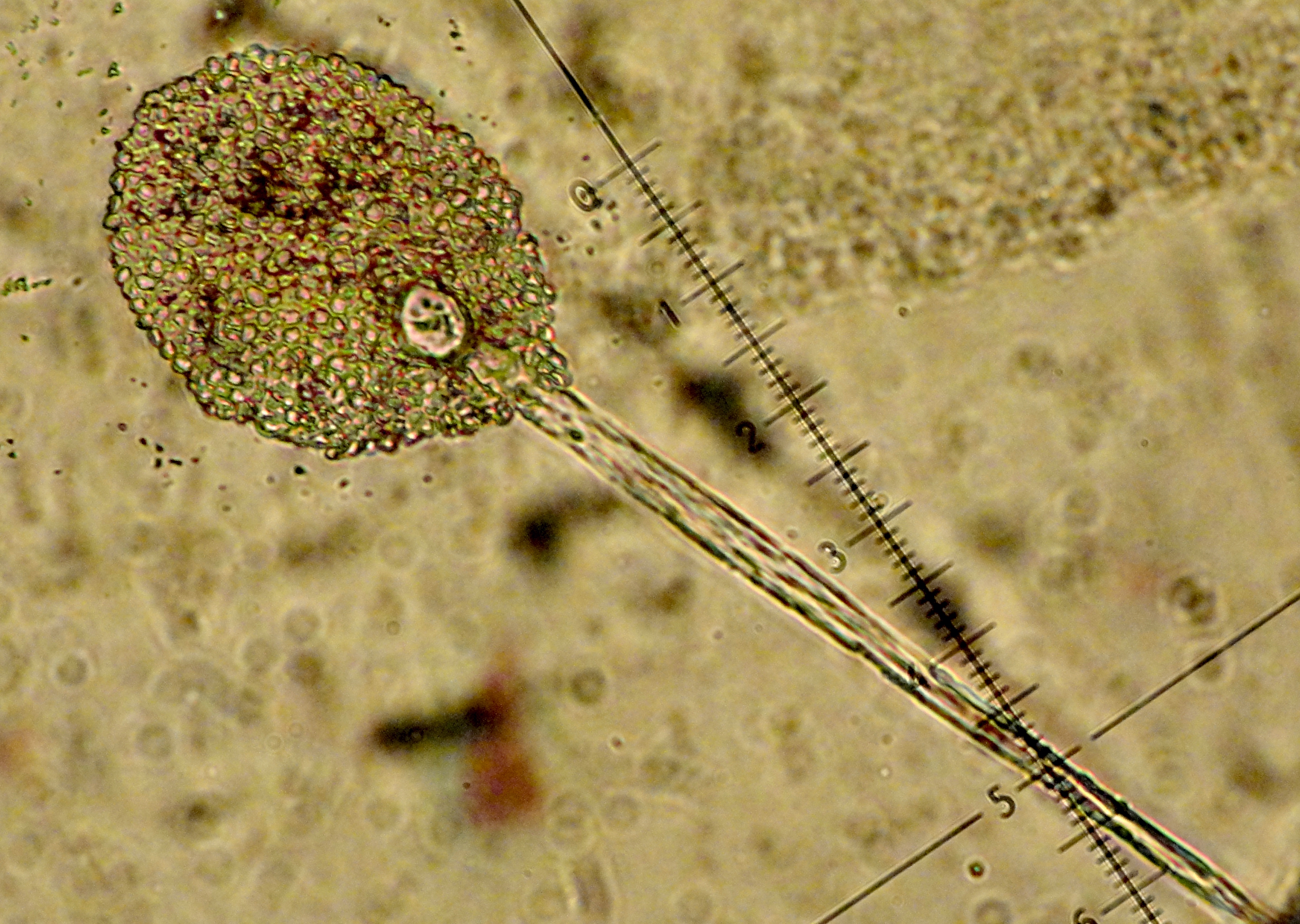
Spore
In biology, a spore is a unit of sexual reproduction, sexual (in fungi) or asexual reproduction that may be adapted for biological dispersal, dispersal and for survival, often for extended periods of time, in unfavourable conditions. Spores form part of the Biological life cycle, life cycles of many plants, algae, fungus, fungi and protozoa. They were thought to have appeared as early as the mid-late Ordovician period as an adaptation of early land plants. Bacterial spores are not part of a sexual cycle, but are resistant structures used for survival under unfavourable conditions. Myxozoan spores release amoeboid infectious germs ("amoebulae") into their hosts for parasitic infection, but also reproduce within the hosts through the pairing of two nuclei within the plasmodium, which develops from the amoebula. In plants, spores are usually haploid and unicellular and are produced by meiosis in the sporangium of a diploid sporophyte. In some rare cases, a diploid spore is also p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seed
In botany, a seed is a plant structure containing an embryo and stored nutrients in a protective coat called a ''testa''. More generally, the term "seed" means anything that can be Sowing, sown, which may include seed and husk or tuber. Seeds are the product of the ripened ovule, after the embryo sac is fertilization, fertilized by Pollen, sperm from pollen, forming a zygote. The embryo within a seed develops from the zygote and grows within the mother plant to a certain size before growth is halted. The formation of the seed is the defining part of the process of reproduction in seed plants (spermatophytes). Other plants such as ferns, mosses and marchantiophyta, liverworts, do not have seeds and use water-dependent means to propagate themselves. Seed plants now dominate biological Ecological niche, niches on land, from forests to grasslands both in hot and cold climates. In the flowering plants, the ovary ripens into a fruit which contains the seed and serves to disseminate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photosynthesis
Photosynthesis ( ) is a system of biological processes by which photosynthetic organisms, such as most plants, algae, and cyanobacteria, convert light energy, typically from sunlight, into the chemical energy necessary to fuel their metabolism. ''Photosynthesis'' usually refers to oxygenic photosynthesis, a process that produces oxygen. Photosynthetic organisms store the chemical energy so produced within intracellular organic compounds (compounds containing carbon) like sugars, glycogen, cellulose and starches. To use this stored chemical energy, an organism's cells metabolize the organic compounds through cellular respiration. Photosynthesis plays a critical role in producing and maintaining the oxygen content of the Earth's atmosphere, and it supplies most of the biological energy necessary for complex life on Earth. Some bacteria also perform anoxygenic photosynthesis, which uses bacteriochlorophyll to split hydrogen sulfide as a reductant instead of water, p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soil
Soil, also commonly referred to as earth, is a mixture of organic matter, minerals, gases, water, and organisms that together support the life of plants and soil organisms. Some scientific definitions distinguish dirt from ''soil'' by restricting the former term specifically to displaced soil. Soil consists of a solid collection of minerals and organic matter (the soil matrix), as well as a porous phase that holds gases (the soil atmosphere) and water (the soil solution). Accordingly, soil is a three- state system of solids, liquids, and gases. Soil is a product of several factors: the influence of climate, relief (elevation, orientation, and slope of terrain), organisms, and the soil's parent materials (original minerals) interacting over time. It continually undergoes development by way of numerous physical, chemical and biological processes, which include weathering with associated erosion. Given its complexity and strong internal connectedness, soil ecologists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients. Root or roots may also refer to: Art, entertainment, and media * ''The Root'' (magazine), an online magazine focusing on African-American culture * The Roots, a location in the video game '' Kya: Dark Lineage'' Films * ''Roots'' (film) (), a 1955 Mexican drama * '' Poor Relatives'', also released as ''Roots'', a 2005 Russian film * ''Roots'', the English title for the 2019 Tamil film '' Sethum Aayiram Pon'' Literature and stage plays * ''Koreni'' (novel) (English: ''The Roots''), a 1954 novel by Serbian author Dobrica Ćosić * ''Roots'' (play), a 1958 play by Arnold Wesker * '' Roots: The Saga of an American Family'', a 1976 novel by Alex Haley about slavery in the United States Music * Root (chord), the fundamental note of a chord * Roots music (other) Groups and individuals * Root (band), a Czech metal band * Root (singer), a Japan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vascular Tissue
Vascular tissue is a complex transporting tissue, formed of more than one cell type, found in vascular plants. The primary components of vascular tissue are the xylem and phloem. These two tissues transport fluid and nutrients internally. There are also two meristems associated with vascular tissue: the vascular cambium and the cork cambium. All the vascular tissues within a particular plant together constitute the vascular tissue system of that plant. The cells in vascular tissue are typically long and slender. Since the xylem and phloem function in the conduction of water, minerals, and nutrients throughout the plant, it is not surprising that their form should be similar to pipes. The individual cells of phloem are connected end-to-end, just as the sections of a pipe might be. As the plant grows, new vascular tissue differentiates in the growing tips of the plant. The new tissue is aligned with existing vascular tissue, maintaining its connection throughout the plant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |