|
Topology Of The Universe
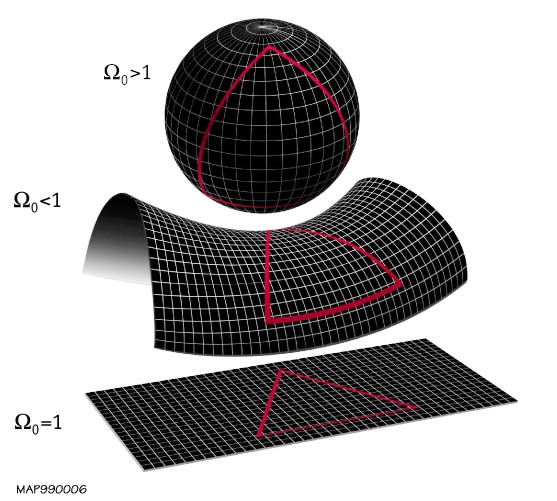
The shape of the universe, in physical cosmology, is the local and global geometry of the universe. The local features of the geometry of the universe are primarily described by its curvature, whereas the topology of the universe describes general global properties of its shape as a continuous object. The spatial curvature is defined by general relativity, which describes how spacetime is curved due to the effect of gravity. The spatial topology cannot be determined from its curvature, due to the fact that there exist locally indistinguishable spaces that may be endowed with different topological invariants. Cosmologists distinguish between the observable universe and the entire universe, the former being a ball-shaped portion of the latter that can, in principle, be accessible by astronomical observations. Assuming the cosmological principle, the observable universe is similar from all contemporary vantage points, which allows cosmologists to discuss properties of the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Cosmology
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of fundamental questions about its Cosmogony, origin, structure, Chronology of the universe, evolution, and ultimate fate.For an overview, see Cosmology as a science originated with the Copernican principle, which implies that astronomical object, celestial bodies obey identical physical laws to those on Earth, and Newtonian mechanics, which first allowed those physical laws to be understood. Physical cosmology, as it is now understood, began with the development in 1915 of Albert Einstein's general relativity, general theory of relativity, followed by major observational discoveries in the 1920s: first, Edwin Hubble discovered that the universe contains a huge number of external Galaxy, galaxies beyond the Milky Way; then, work by Vesto Sli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NASA
The National Aeronautics and Space Administration (NASA ) is an independent agency of the US federal government responsible for the civil space program, aeronautics research, and space research. NASA was established in 1958, succeeding the National Advisory Committee for Aeronautics (NACA), to give the U.S. space development effort a distinctly civilian orientation, emphasizing peaceful applications in space science. NASA has since led most American space exploration, including Project Mercury, Project Gemini, the 1968-1972 Apollo Moon landing missions, the Skylab space station, and the Space Shuttle. NASA supports the International Space Station and oversees the development of the Orion spacecraft and the Space Launch System for the crewed lunar Artemis program, Commercial Crew spacecraft, and the planned Lunar Gateway space station. The agency is also responsible for the Launch Services Program, which provides oversight of launch operations and countdown management f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous
Homogeneity and heterogeneity are concepts often used in the sciences and statistics relating to the uniformity of a substance or organism. A material or image that is homogeneous is uniform in composition or character (i.e. color, shape, size, weight, height, distribution, texture, language, income, disease, temperature, radioactivity, architectural design, etc.); one that is heterogeneous is distinctly nonuniform in at least one of these qualities. Heterogeneous Mixtures, in chemistry, is where certain elements are unwillingly combined and, when given the option, will separate. Etymology and spelling The words ''homogeneous'' and ''heterogeneous'' come from Medieval Latin ''homogeneus'' and ''heterogeneus'', from Ancient Greek ὁμογενής (''homogenēs'') and ἑτερογενής (''heterogenēs''), from ὁμός (''homos'', “same”) and ἕτερος (''heteros'', “other, another, different”) respectively, followed by γένος (''genos'', “kind”); - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an isotropic vector is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosmic Microwave Background
In Big Bang cosmology the cosmic microwave background (CMB, CMBR) is electromagnetic radiation that is a remnant from an early stage of the universe, also known as "relic radiation". The CMB is faint cosmic background radiation filling all space. It is an important source of data on the early universe because it is the oldest electromagnetic radiation in the universe, dating to the epoch of recombination when the first atoms were formed. With a traditional optical telescope, the space between stars and galaxies (the background) is completely dark (see: Olbers' paradox). However, a sufficiently sensitive radio telescope shows a faint background brightness, or glow, almost uniform, that is not associated with any star, galaxy, or other object. This glow is strongest in the microwave region of the radio spectrum. The accidental discovery of the CMB in 1965 by American radio astronomers Arno Penzias and Robert Wilson was the culmination of work initiated in the 1940s, and earned th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Radiation
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic field, electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, Light, (visible) light, ultraviolet, X-rays, and gamma rays. All of these waves form part of the electromagnetic spectrum. Classical electromagnetism, Classically, electromagnetic radiation consists of electromagnetic waves, which are synchronized oscillations of electric field, electric and magnetic fields. Depending on the frequency of oscillation, different wavelengths of electromagnetic spectrum are produced. In a vacuum, electromagnetic waves travel at the speed of light, commonly denoted ''c''. In homogeneous, isotropic media, the oscillations of the two fields are perpendicular to each other and perpendicular to the direction of energy and wave propagation, forming a transverse wave. The position of an electromagnetic wave w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big Bang
The Big Bang event is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models of the Big Bang explain the evolution of the observable universe from the earliest known periods through its subsequent large-scale form. These models offer a comprehensive explanation for a broad range of observed phenomena, including the abundance of light elements, the cosmic microwave background (CMB) radiation, and large-scale structure. The overall uniformity of the Universe, known as the flatness problem, is explained through cosmic inflation: a sudden and very rapid expansion of space during the earliest moments. However, physics currently lacks a widely accepted theory of quantum gravity that can successfully model the earliest conditions of the Big Bang. Crucially, these models are compatible with the Hubble–Lemaître law—the observation that the farther away a galaxy is, the faster it is mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Redshift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and simultaneous increase in frequency and energy, is known as a negative redshift, or blueshift. The terms derive from the colours red and blue which form the extremes of the visible light spectrum. In astronomy and cosmology, the three main causes of electromagnetic redshift are # The radiation travels between objects which are moving apart (" relativistic" redshift, an example of the relativistic Doppler effect) #The radiation travels towards an object in a weaker gravitational potential, i.e. towards an object in less strongly curved (flatter) spacetime (gravitational redshift) #The radiation travels through expanding space (cosmological redshift). The observation that all sufficiently distant light sources show redshift corresponding to their distance from Earth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Half-plane Model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H = \, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry. Equivalently the Poincaré half-plane model is sometimes described as a complex plane where the imaginary part (the ''y'' coordinate mentioned above) is positive. The Poincaré half-plane model is named after Henri Poincaré, but it originated with Eugenio Beltrami who used it, along with the Klein model and the Poincaré disk model, to show that hyperbolic geometry was equiconsistent with Euclidean geometry. This model is conformal which means that the angles measured at a point are the same in the model as they are in the actual hyperbolic plane. The Cayley transform provides an isometry between the half-plane model and the Poincaré disk model. This model can be generalized to model an n+1 dimensional hyperbolic space by replacing the real number ''x'' by a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Space (topology)
In topology and related areas of mathematics, the quotient space of a topological space under a given equivalence relation is a new topological space constructed by endowing the quotient set of the original topological space with the quotient topology, that is, with the finest topology that makes continuous the canonical projection map (the function that maps points to their equivalence classes). In other words, a subset of a quotient space is open if and only if its preimage under the canonical projection map is open in the original topological space. Intuitively speaking, the points of each equivalence class are or "glued together" for forming a new topological space. For example, identifying the points of a sphere that belong to the same diameter produces the projective plane as a quotient space. Definition Let \left(X, \tau_X\right) be a topological space, and let \,\sim\, be an equivalence relation on X. The quotient set, Y = X / \sim\, is the set of equivalence cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homology Sphere
Homology may refer to: Sciences Biology *Homology (biology), any characteristic of biological organisms that is derived from a common ancestor *Sequence homology, biological homology between DNA, RNA, or protein sequences *Homologous chromosomes, chromosomes in a biological cell that pair up (synapse) during meiosis *Homologous recombination, genetic recombination in which nucleotide sequences are exchanged between molecules of DNA *Homologous desensitization, a receptor decreases its response to a signalling molecule when that agonist is in high concentration *Homology modeling, a method of protein structure prediction Chemistry *Homology (chemistry), the relationship between compounds in a homologous series *Homologous series, a series of organic compounds having different quantities of a repeated unit *Homologous temperature, the temperature of a material as a fraction of its absolute melting point *Homologation reaction, a chemical reaction which produces the next lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |