|
Topological Games
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connecte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Möbius Strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip. As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Property
In topology and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms. Alternatively, a topological property is a proper class of topological spaces which is closed under homeomorphisms. That is, a property of spaces is a topological property if whenever a space ''X'' possesses that property every space homeomorphic to ''X'' possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets. A common problem in topology is to decide whether two topological spaces are homeomorphic or not. To prove that two spaces are ''not'' homeomorphic, it is sufficient to find a topological property which is not shared by them. Properties of topological properties A property P is: * Hereditary, if for every topological space (X, \mathcal) and X' \subset X, the subspace (X', \mathcal, X') has property P. * Weakly hereditary, if for e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
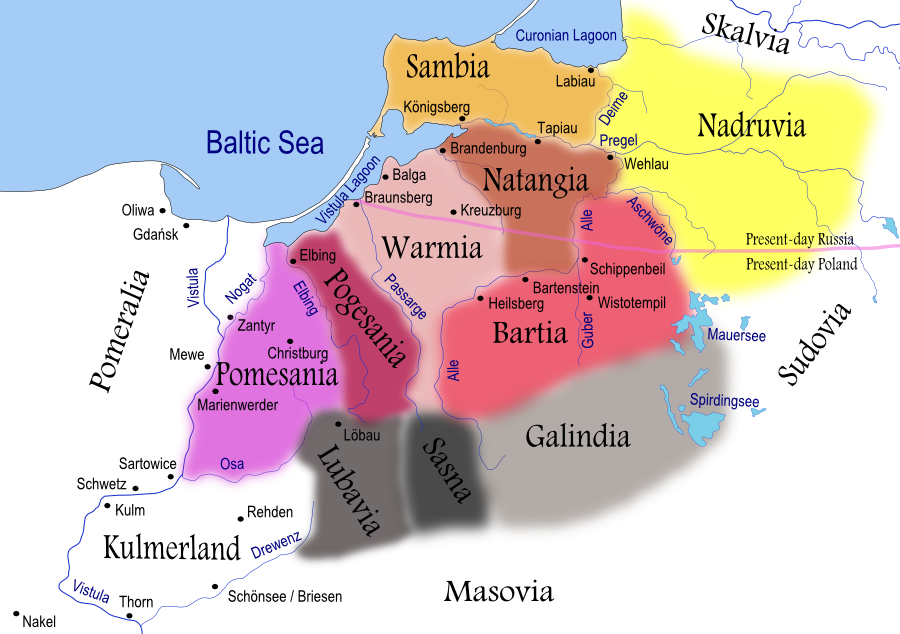
Kaliningrad
Kaliningrad ( ; rus, Калининград, p=kəlʲɪnʲɪnˈɡrat, links=y), until 1946 known as Königsberg (; rus, Кёнигсберг, Kyonigsberg, ˈkʲɵnʲɪɡzbɛrk; rus, Короле́вец, Korolevets), is the largest city and administrative centre of Kaliningrad Oblast, a Russian semi-exclave between Lithuania and Poland. The city sits about west from mainland Russia. The city is situated on the Pregolya River, at the head of the Vistula Lagoon on the Baltic Sea, and is the only ice-free port of Russia and the Baltic states on the Baltic Sea. Its population in 2020 was 489,359, with up to 800,000 residents in the urban agglomeration. Kaliningrad is the second-largest city in the Northwestern Federal District, after Saint Petersburg, the third-largest city in the Baltic region, and the seventh-largest city on the Baltic Sea. The settlement of modern-day Kaliningrad was founded in 1255 on the site of the ancient Old Prussian settlement ''Twangste'' by th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trefoil Knot Arb
A trefoil () is a graphic form composed of the outline of three overlapping rings, used in architecture and Christian symbolism, among other areas. The term is also applied to other symbols with a threefold shape. A similar shape with four rings is called a quatrefoil. Architecture Ornamentation 'Trefoil' is a term in Gothic architecture given to the ornamental foliation or cusping introduced in the heads of window-lights, tracery, and panellings, in which the centre takes the form of a three-lobed leaf (formed from three partially overlapping circles). One of the earliest examples is in the plate tracery at Winchester Cathedral (1222–1235). The fourfold version of an architectural trefoil is a quatrefoil. A simple trefoil shape in itself can be symbolic of the Trinity, while a trefoil combined with an equilateral triangle was also a moderately common symbol of the Christian Trinity during the late Middle Ages in some parts of Europe, similar to a barbed quatrefoil. Two for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johann Benedict Listing
Johann Benedict Listing (25 July 1808 – 24 December 1882) was a German mathematician. J. B. Listing was born in Frankfurt and died in Göttingen. He first introduced the term "topology" to replace the older term "geometria situs" (also called sometimes "Analysis situs"), in a famous article published in 1847, although he had used the term in correspondence some years earlier. He (independently) discovered the properties of the Möbius strip, half-twisted strip at the same time (1858) as August Ferdinand Möbius, and went further in exploring the properties of strips with higher-order twists (paradromic rings). He discovered topological invariants which came to be called Listing numbers.Charles Sanders Peirce, Peirce, C. S., 1992, ''Charles Sanders Peirce bibliography#RLT, Reasoning and the Logic of Things: The Cambridge Conference Lectures of 1898'', edited with introduction by Kenneth Laine Ketner and with commentary by Hilary Putnam, who discusses Listing numbers starting on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by \chi ( Greek lower-case letter chi). The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico. Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology and, more abstractly, homological algebra. Polyhedra The Euler characteristic \chi was classically defined for the surfaces of polyhedra, acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seven Bridges Of Königsberg
The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1736 laid the foundations of graph theory and prefigured the idea of topology. The city of Königsberg in Prussia (now Kaliningrad, Russia) was set on both sides of the Pregel River, and included two large islands—Kneiphof and Lomse—which were connected to each other, and to the two mainland portions of the city, by seven bridges. The problem was to devise a walk through the city that would cross each of those bridges once and only once. By way of specifying the logical task unambiguously, solutions involving either # reaching an island or mainland bank other than via one of the bridges, or # accessing any bridge without crossing to its other end are explicitly unacceptable. Euler proved that the problem has no solution. The difficulty he faced was the development of a suitable technique of analysis, and of subsequent tests that established this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." Euler is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gottfried Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathematics. He wrote works on philosophy, theology, ethics, politics, law, history and philology. Leibniz also made major contributions to physics and technology, and anticipated notions that surfaced much later in probability theory, biology, medicine, geology, psychology, linguistics and computer science. In addition, he contributed to the field of library science: while serving as overseer of the Wolfenbüttel library in Germany, he devised a cataloging system that would have served as a guide for many of Europe's largest libraries. Leibniz's contributions to this vast array of subjects were scattered in various learned journals, in tens of thousands of letters and in unpublished manuscripts. He wrote in several languages, primarily in Latin, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected. When a disconnected object can be split naturally into connected pieces, each piece is usually called a ''component'' (or ''connected component''). Connectedness in topology A topological space is said to be ''connected'' if it is not the union of two disjoint nonempty open sets. A set is open if it contains no point lying on its boundary; thus, in an informal, intuitive sense, the fact that a space can be partitioned into disjoint open sets suggests that the boundary between the two sets is not part of the space, and thus splits it into two separate pieces. Other notions of connectedness Fields of mathematics are typically concerned with special kinds of objects. Often such an object is said to be ''connected'' if, when it is considered as a topological space, it is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact (topology)
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |