|
Thin-film Equation
In fluid mechanics, the thin-film equation is a partial differential equation that approximately predicts the time evolution of the thickness of a liquid film that lies on a surface. The equation is derived via lubrication theory which is based on the assumption that the length-scales in the surface directions are significantly larger than in the direction normal to the surface. In the non-dimensional form of the Navier-Stokes equation the requirement is that terms of order and are negligible, where is the aspect ratio and is the Reynolds number. This significantly simplifies the governing equations. However, lubrication theory, as the name suggests, is typically derived for flow between two solid surfaces, hence the liquid forms a lubricating layer. The thin-film equation holds when there is a single free surface. With two free surfaces, the flow must be treated as a viscous sheet. Definition The basic form of a 2-dimensional thin film equation isA. Oron, S. H. Davis, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Mechanics
Fluid mechanics is the branch of physics concerned with the mechanics of fluids ( liquids, gases, and plasmas) and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology. It can be divided into fluid statics, the study of fluids at rest; and fluid dynamics, the study of the effect of forces on fluid motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a ''macroscopic'' viewpoint rather than from ''microscopic''. Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hele-Shaw Flow
Hele-Shaw flow is defined as Stokes flow between two parallel flat plates separated by an infinitesimally small gap, named after Henry Selby Hele-Shaw, who studied the problem in 1898. Various problems in fluid mechanics can be approximated to Hele-Shaw flows and thus the research of these flows is of importance. Approximation to Hele-Shaw flow is specifically important to micro-flows. This is due to manufacturing techniques, which creates shallow planar configurations, and the typically low Reynolds numbers of micro-flows. The governing equation of Hele-Shaw flows is identical to that of the inviscid potential flow and to the flow of fluid through a porous medium (Darcy's law). It thus permits visualization of this kind of flow in two dimensions. Mathematical formulation of Hele-Shaw flows Let x, y be the directions parallel to the flat plates, and z the perpendicular direction, with H being the gap between the plates (at z=0, H). When the gap between plates is asymptotically sm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lubrication Theory
In fluid dynamics, lubrication theory describes the flow of fluids (liquids or gases) in a geometry in which one dimension is significantly smaller than the others. An example is the flow above air hockey tables, where the thickness of the air layer beneath the puck is much smaller than the dimensions of the puck itself. Internal flows are those where the fluid is fully bounded. Internal flow lubrication theory has many industrial applications because of its role in the design of fluid bearings. Here a key goal of lubrication theory is to determine the pressure distribution in the fluid volume, and hence the forces on the bearing components. The working fluid in this case is often termed a lubricant. Free film lubrication theory is concerned with the case in which one of the surfaces containing the fluid is a free surface. In that case the position of the free surface is itself unknown, and one goal of lubrication theory is then to determine this. Examples include the flow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Washburn's Equation
In physics, Washburn's equation describes capillary flow in a bundle of parallel cylindrical tubes; it is extended with some issues also to imbibition into porous materials. The equation is named after Edward Wight Washburn; also known as Lucas–Washburn equation, considering that Richard Lucas wrote a similar paper three years earlier, or the Bell-Cameron-Lucas-Washburn equation, considering J.M. Bell and F.K. Cameron's discovery of the form of the equation in 1906. Derivation In its most general form the Lucas Washburn equation describes the penetration length (L) of a liquid into a capillary pore or tube with time t as L=(Dt)^, where D is a simplified diffusion coefficient. This relationship, which holds true for a variety of situations, captures the essence of Lucas and Washburn's equation and shows that capillary penetration and fluid transport through porous structures exhibit diffusive behaviour akin to that which occurs in numerous physical and chemical systems. The dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contact Angle
The contact angle is the angle, conventionally measured through the liquid, where a liquid–vapor interface meets a solid surface. It quantifies the wettability of a solid surface by a liquid via the Young equation. A given system of solid, liquid, and vapor at a given temperature and pressure has a unique equilibrium contact angle. However, in practice a dynamic phenomenon of contact angle hysteresis is often observed, ranging from the advancing (maximal) contact angle to the receding (minimal) contact angle. The equilibrium contact is within those values, and can be calculated from them. The equilibrium contact angle reflects the relative strength of the liquid, solid, and vapour molecular interaction. The contact angle depends upon the medium above the free surface of the liquid, and the nature of the liquid and solid in contact. It is independent of the inclination of solid to the liquid surface. It changes with surface tension and hence with the temperature and purity of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sessile Drop Technique
image:Contact angle.svg, 400px, Fig 1: An illustration of the sessile drop technique with a liquid droplet partially wetting a solid substrate. is the contact angle, and represent the solid–gas, gas–liquid, and liquid–solid interfaces, respectively. In materials science, the sessile drop technique is a method used for the characterization of solid surface energy, surface energies, and in some cases, aspects of liquid surface energies. The main premise of the method is that by placing a droplet of liquid with a known surface energy and contact angle, the surface energy of the solid substrate can be calculated. The liquid used for such experiments is referred to as the probe liquid, and the use of several different probe liquids is required. Probe liquid The surface energy is measured in units of Joules per area, which is equivalent in the case of liquids to surface tension, measured in Newtons per meter. The overall surface tension/energy of a liquid can be acquired th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere (forming a great circle), so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a '' hemisphere''. Volume and surface area The volume of the spherical cap and the area of the curved surface may be calculated using combinations of * The radius r of the sphere * The radius a of the base of the cap * The height h of the cap * The polar angle \theta between the rays from the center of the sphere to the apex of the cap (the pole) and the edge of the disk forming the base of the cap If \phi denotes the latitude in geographic coordinates, then \theta+\phi = \pi/2 = 90^\circ\,, and \cos \theta = \sin \phi. The relationship between h and r is relevant as long as 0\le h\le2r. For example, the red section of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraboloid Of Revolution
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid by a plane parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The paraboloid is hyperbolic if the factors are real; elliptic if the factors are complex co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bingham Plastic
A Bingham plastic is a viscoplastic material that behaves as a rigid body at low stresses but flows as a viscous fluid at high stress. It is named after Eugene C. Bingham who proposed its mathematical form. It is used as a common mathematical model of mud flow in drilling engineering, and in the handling of slurries. A common example is toothpaste, which will not be extruded until a certain pressure is applied to the tube. It is then pushed out as a relatively coherent plug. Explanation Figure 1 shows a graph of the behaviour of an ordinary viscous (or Newtonian) fluid in red, for example in a pipe. If the pressure at one end of a pipe is increased this produces a stress on the fluid tending to make it move (called the shear stress) and the volumetric flow rate increases proportionally. However, for a Bingham Plastic fluid (in blue), stress can be applied but it will not flow until a certain value, the yield stress, is reached. Beyond this point the flow rate increases st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transition
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition At the phase transition point for a substance, for instance the boiling point, the two phases involved - liquid and vapor, have id ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
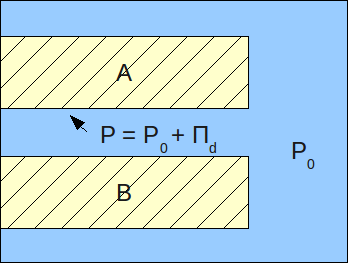
Disjoining Pressure
In surface chemistry, disjoining pressure (symbol ) according to an IUPAC definition arises from an attractive interaction between two surfaces. For two flat and parallel surfaces, the value of the disjoining pressure (i.e., the force per unit area) can be calculated as the derivative of the Gibbs energy of interaction per unit area in respect to distance (in the direction normal to that of the interacting surfaces). There is also a related concept of disjoining force, which can be viewed as disjoining pressure times the surface area of the interacting surfaces. The concept of disjoining pressure was introduced by Derjaguin (1936) as the difference between the pressure in a region of a phase adjacent to a surface confining it, and the pressure in the bulk of this phase. Description Disjoining pressure can be expressed as:Hans-Jürgen Butt, Karlheinz Graf, Michael Kappl,"Physics and chemistry of interfaces", John Wiley & Sons Canada, Ltd., 1 edition, 2003, page 9(Google book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |