|
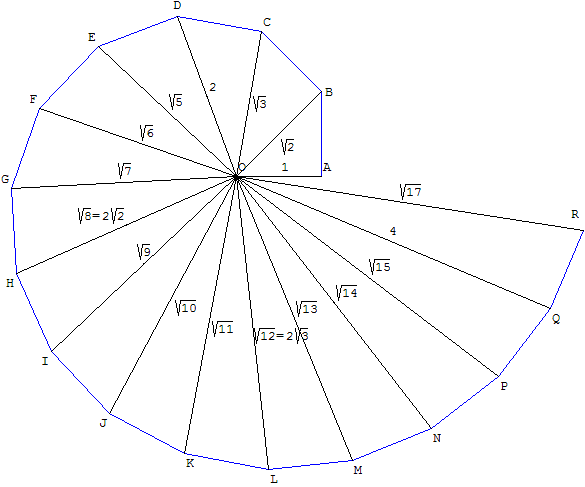
Theodorus Of Cyrene
Theodorus of Cyrene ( el, Θεόδωρος ὁ Κυρηναῖος) was an ancient Greek mathematician who lived during the 5th century BC. The only first-hand accounts of him that survive are in three of Plato's dialogues: the '' Theaetetus'', the ''Sophist'', and the ''Statesman''. In the former dialogue, he posits a mathematical theorem now known as the Spiral of Theodorus. Life Little is known as Theodorus' biography beyond what can be inferred from Plato's dialogues. He was born in the northern African colony of Cyrene, and apparently taught both there and in Athens. He complains of old age in the ''Theaetetus'', the dramatic date of 399 BC of which suggests his period of flourishing to have occurred in the mid-5th century. The text also associates him with the sophist Protagoras, with whom he claims to have studied before turning to geometry. A dubious tradition repeated among ancient biographers like Diogenes Laërtius held that Plato later studied with him in Cyrene, Libya ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyrene, Libya
Cyrene ( ) or Kyrene ( ; grc, Κυρήνη, Kyrḗnē, arb, شحات, Shaḥāt), was an ancient Greek and later Roman city near present-day Shahhat, Libya. It was the oldest and most important of the five Greek cities, known as the pentapoleis, in the region. It gave eastern Libya the classical name ''Cyrenaica'' that it has retained to modern times. Located nearby is the ancient Necropolis of Cyrene. The traditional founder of the city was Battus the Lacedemonian, though the exact relationship between the fledgling city and other cities has led historians to question that narrative. Particularly, the idea that Thera was the sole "mother city" is disputed; and the relationship with other cities, such as Sparta and Samnium merchants, is unclear. Cyrene lies in a lush valley in the Jebel Akhdar uplands. The city was named after a spring, Kyre, which the Greeks consecrated to Apollo. It became the seat of the Cyrenaics, a famous school of philosophy in the fourth century BC, fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Continued Fraction
In mathematics, an infinite periodic continued fraction is a continued fraction that can be placed in the form : x = a_0 + \cfrac where the initial block of ''k'' + 1 partial denominators is followed by a block 'a''''k''+1, ''a''''k''+2,...''a''''k''+''m''of partial denominators that repeats over and over again, ''ad infinitum''. For example, \sqrt2 can be expanded to a periodic continued fraction, namely as ,2,2,2,... The partial denominators can in general be any real or complex numbers. That general case is treated in the article convergence problem. The remainder of this article is devoted to the subject of simple continued fractions that are also periodic. In other words, the remainder of this article assumes that all the partial denominators ''a''''i'' (''i'' ≥ 1) are positive integers. Purely periodic and periodic fractions Since all the partial numerators in a regular continued fraction are equal to unity we can adopt a shorthand notation in which t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancient Greek Mathematicians
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean from Italy to North Africa but were united by Greek culture and the Greek language. The word "mathematics" itself derives from the grc, , máthēma , meaning "subject of instruction". The study of mathematics for its own sake and the use of generalized mathematical theories and proofs is an important difference between Greek mathematics and those of preceding civilizations. Origins of Greek mathematics The origin of Greek mathematics is not well documented. The earliest advanced civilizations in Greece and in Europe were the Minoan and later Mycenaean civilizations, both of which flourished during the 2nd millennium BCE. While these civilizations possessed writing an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wilbur Knorr
Wilbur Richard Knorr (August 29, 1945 – March 18, 1997) was an American historian of mathematics and a professor in the departments of philosophy and classics at Stanford University. He has been called "one of the most profound and certainly the most provocative historian of Greek mathematics" of the 20th century. Biography Knorr was born August 29, 1945, in Richmond Hill, Queens. He did his undergraduate studies at Harvard University from 1963 to 1966 and stayed there for his Ph.D., which he received in 1973 under the supervision of John Emery Murdoch and G. E. L. Owen... After postdoctoral studies at Cambridge University, he taught at Brooklyn College, but lost his position when the college's Downtown Brooklyn campus was closed as part of New York's mid-1970s fiscal crisis. After taking a temporary position at the Institute for Advanced Study, he joined the Stanford faculty as an assistant professor in 1979, was tenured there in 1983, and was promoted to full professor in 199 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Irrational
In mathematics, a quadratic irrational number (also known as a quadratic irrational, a quadratic irrationality or quadratic surd) is an irrational number that is the solution to some quadratic equation with rational coefficients which is irreducible over the rational number In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...s. Since fractions in the coefficients of a quadratic equation can be cleared by multiplying both sides by their least common denominator, a quadratic irrational is an irrational root of some quadratic equation with integer coefficients. The quadratic irrational numbers, a subset of the complex numbers, are algebraic numbers of Algebraic number#Properties, degree 2, and can therefore be expressed as :, for integers ; with , and non-zero, and with Square-free in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Speakers In Plato's Dialogues
following is a list of the speakers found in the dialogues traditionally ascribed to Plato, including extensively quoted, indirect and conjured speakers. Dialogues, as well as Platonic '' Epistles'' and ''Epigrams'', in which these individuals appear dramatically but do not speak are listed separately. ;Unnamed speakers Notes Bibliography * Debra Nails. ''The People of Plato: A Prosopography of Plato and Other Socratics''. Hackett Publishing, 2002. . * Plato Plato ( ; grc-gre, Πλάτων ; 428/427 or 424/423 – 348/347 BC) was a Greek philosopher born in Athens during the Classical period in Ancient Greece. He founded the Platonist school of thought and the Academy, the first institution .... ''Complete Works''. Ed: John M. Cooper. Hackett Publishing, 1997. {{Socrates navbox * * Platos Dialogues Speakers in Plato's dialogues ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chronology Of Ancient Greek Mathematicians
This is a chronology of ancient Greek mathematicians Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathem .... See also * * * * * References {{DEFAULTSORT:Chronology Of Ancient Greek Mathematicians Ancient Greek mathematicians Greek mathematics History of geometry History of mathematics Mathematics timelines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nth Root
In mathematics, a radicand, also known as an nth root, of a number ''x'' is a number ''r'' which, when raised to the power ''n'', yields ''x'': :r^n = x, where ''n'' is a positive integer, sometimes called the ''degree'' of the root. A root of degree 2 is called a ''square root'' and a root of degree 3, a ''cube root''. Roots of higher degree are referred by using ordinal numbers, as in ''fourth root'', ''twentieth root'', etc. The computation of an th root is a root extraction. For example, 3 is a square root of 9, since 3 = 9, and −3 is also a square root of 9, since (−3) = 9. Any non-zero number considered as a complex number has different complex th roots, including the real ones (at most two). The th root of 0 is zero for all positive integers , since . In particular, if is even and is a positive real number, one of its th roots is real and positive, one is negative, and the others (when ) are non-real complex numbers; if is even and is a negative real numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scholia
Scholia (singular scholium or scholion, from grc, σχόλιον, "comment, interpretation") are grammatical, critical, or explanatory comments – original or copied from prior commentaries – which are inserted in the margin of the manuscript of ancient authors, as glosses. One who writes scholia is a scholiast. The earliest attested use of the word dates to the 1st century BC. History Ancient scholia are important sources of information about many aspects of the ancient world, especially ancient literary history. The earliest scholia, usually anonymous, date to the 5th or 4th century BC (such as the ''scholia minora'' to the ''Iliad''). The practice of compiling scholia continued to late Byzantine times, outstanding examples being Archbishop Eustathius' massive commentaries to Homer in the 12th century and the ''scholia recentiora'' of Thomas Magister, Demetrius Triclinius and Manuel Moschopoulos in the 14th. Scholia were altered by successive copyists an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Escargot Pythagore
Snails are considered edible in many areas such as the Mediterranean region, Africa, or Southeast Asia, while in other cultures, snails are seen as a taboo food. In American English, edible land snails are also called escargot, taken from the French word for 'snail,' and the production of snails for consumption is called snail farming or heliciculture. Snails as a food date back to ancient times, with numerous cultures worldwide having traditions and practices that attest to their consumption. The snails are collected after the rains and are put to "purge" (fasting). In the past, the consumption of snails had a marked seasonality, from April to June. However, thanks to snail breeding techniques, today they are available all year round. Heliciculture occurs mainly in Spain, France, and Italy, which are also the countries with the greatest culinary tradition of the snail. Although throughout history, the snail has had little value in the kitchen because it is considered "poverty foo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling or experimentation, which represent the values of a function for a limited number of values of the independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gain in simplicity may outweigh the loss from interpolation error and give better performance in ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip J
Philip, also Phillip, is a male given name, derived from the Greek (''Philippos'', lit. "horse-loving" or "fond of horses"), from a compound of (''philos'', "dear", "loved", "loving") and (''hippos'', "horse"). Prominent Philips who popularized the name include kings of Macedonia and one of the apostles of early Christianity. ''Philip'' has many alternative spellings. One derivation often used as a surname is Phillips. It was also found during ancient Greek times with two Ps as Philippides and Philippos. It has many diminutive (or even hypocoristic) forms including Phil, Philly, Lip, Pip, Pep or Peps. There are also feminine forms such as Philippine and Philippa. Antiquity Kings of Macedon * Philip I of Macedon * Philip II of Macedon, father of Alexander the Great * Philip III of Macedon, half-brother of Alexander the Great * Philip IV of Macedon * Philip V of Macedon New Testament * Philip the Apostle * Philip the Evangelist Others * Philippus of Croton (c. 6th ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |