|
Tetrastix
In geometry, it is possible to fill 3/4 of the volume of three-dimensional Euclidean space by three sets of infinitely-long square prisms aligned with the three coordinate axes, leaving cubical voids; John Horton Conway, Heidi Burgiel and Chaim Goodman-Strauss have named this structure tetrastix. Applications The motivation for some of the early studies of this structure was for its applications in the crystallography of crystal structures formed by rod-shaped molecules. Shrinking the square cross-sections of the prisms slightly causes the remaining space, consisting of the cubical voids, to become linked up into a single polyhedral set, bounded by axis-parallel faces. Polyhedra constructed in this way from finitely many prisms provide examples of axis-parallel polyhedra with n vertices and faces that require \Omega(n^) pieces when subdivided into convex pieces; they have been called Thurston polyhedra, after William Thurston, who suggested using these shapes for this lower bound ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrastix
In geometry, it is possible to fill 3/4 of the volume of three-dimensional Euclidean space by three sets of infinitely-long square prisms aligned with the three coordinate axes, leaving cubical voids; John Horton Conway, Heidi Burgiel and Chaim Goodman-Strauss have named this structure tetrastix. Applications The motivation for some of the early studies of this structure was for its applications in the crystallography of crystal structures formed by rod-shaped molecules. Shrinking the square cross-sections of the prisms slightly causes the remaining space, consisting of the cubical voids, to become linked up into a single polyhedral set, bounded by axis-parallel faces. Polyhedra constructed in this way from finitely many prisms provide examples of axis-parallel polyhedra with n vertices and faces that require \Omega(n^) pieces when subdivided into convex pieces; they have been called Thurston polyhedra, after William Thurston, who suggested using these shapes for this lower bound ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
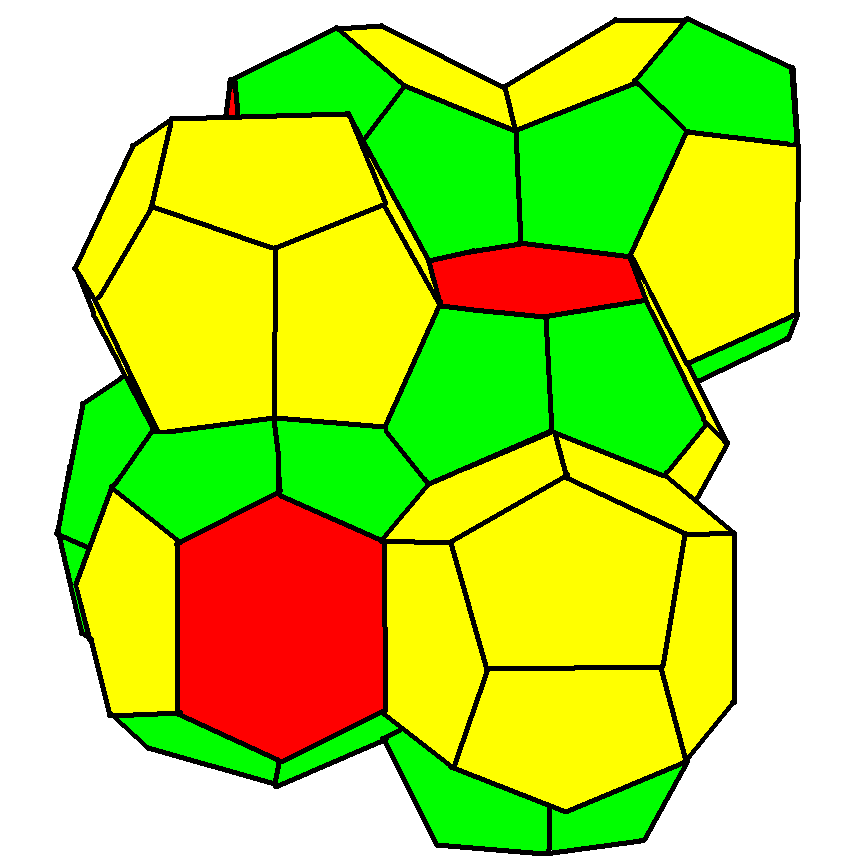
Weaire–Phelan Structure
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure. History and the Kelvin problem In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro, it was not proven until the work of Thomas C. Hales in 1999. In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubble foam? This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexastix
Hexastix is a symmetric arrangement of non-intersecting prisms, that when extended infinitely, fill exactly 3/4 of space. The prisms in a hexastix arrangement are all parallel to 4 directions on the body-centered cubic lattice. In '' The Symmetries of Things'', John Horton Conway, Heidi Burgiel, and Chaim Goodman-Strauss named this structure hexastix. Applications The hexastix arrangement has found use in mathematics, crystallography, reticular chemistry, puzzle design, and art. Michael O'Keeffe (chemist) and associates define this structure as one of the 6 possible invariant cubic rod packing arrangements. O’Keefe classifies this arrangement as the ''Γ'' or Garnet rod packing, and describes it as the densest possible cubic rod packing. Rod packings are used to classify chains of atoms in crystal structures, and in the develop of materials like metal–organic frameworks. It has been proposed that stratum corneum’s structure could be modeled using the hexastix cylinder packi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Burr Puzzle
A burr puzzle is an interlocking puzzle consisting of notched sticks, combined to make one three-dimensional, usually symmetrical unit. These puzzles are traditionally made of wood, but versions made of plastic or metal can also be found. Quality burr puzzles are usually precision-made for easy sliding and accurate fitting of the pieces. In recent years the definition of "burr" is expanding, as puzzle designers use this name for puzzles not necessarily of stick-based pieces. History The term "burr" is first mentioned in a 1928 book by Edwin Wyatt, but the text implies that it was commonly used before. The term is attributed to the finished shape of many of these puzzles, resembling a seed burr. The origin of burr puzzles is unknown. The first known record appears in a 1698 engraving used as a title page of Chambers's Cyclopaedia. Later records can be found in German catalogs from the late 18th century and early 19th century. There are claims of the burr being a Chinese inventio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mucube
In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either skew regular faces or skew regular vertex figures. History According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to finite regular skew polyhedra in 4-dimensions, and infinite regular skew apeirohedra in 3-dimensions (described here). Coxeter identified 3 forms, with planar faces and skew vertex figures, two are complements of each other. They are all named with a modified Schläfli symbol , where there are ''l''-gonal faces, ''m'' faces around each vertex, with ''holes'' identified as ''n''-gonal missing faces. Coxeter offered a modified Schläfli symbol for these figures, with implying the vertex figure, ''m'' l-gons around a vertex, and ''n''-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes. The regular skew polyhedra, represented by , follow this equation: * 2 sin(/''l'') · ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexastix
Hexastix is a symmetric arrangement of non-intersecting prisms, that when extended infinitely, fill exactly 3/4 of space. The prisms in a hexastix arrangement are all parallel to 4 directions on the body-centered cubic lattice. In '' The Symmetries of Things'', John Horton Conway, Heidi Burgiel, and Chaim Goodman-Strauss named this structure hexastix. Applications The hexastix arrangement has found use in mathematics, crystallography, reticular chemistry, puzzle design, and art. Michael O'Keeffe (chemist) and associates define this structure as one of the 6 possible invariant cubic rod packing arrangements. O’Keefe classifies this arrangement as the ''Γ'' or Garnet rod packing, and describes it as the densest possible cubic rod packing. Rod packings are used to classify chains of atoms in crystal structures, and in the develop of materials like metal–organic frameworks. It has been proposed that stratum corneum’s structure could be modeled using the hexastix cylinder packi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Keller's Conjecture
In geometry, Keller's conjecture is the conjecture that in any tiling of -dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire -dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration. This conjecture was introduced by , after whom it is named. A breakthrough by showed that it is false in ten or more dimensions, and after subsequent refinements, it is now known to be true in spaces of dimension at most seven and false in all higher dimensions. The proofs of these results use a reformulation of the problem in terms of the clique number of certain graphs now known as Keller graphs. The related Minkowski lattice cube-tiling conjecture states that whenever a tiling of space by identical cubes has the additional property that the cubes' centers form a lattice, some cubes must meet face-to-face. It was proved by György Hajà ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oskar Perron
Oskar Perron (7 May 1880 – 22 February 1975) was a German mathematician. He was a professor at the University of Heidelberg from 1914 to 1922 and at the University of Munich from 1922 to 1951. He made numerous contributions to differential equations and partial differential equations, including the Perron method to solve the Dirichlet problem for elliptic partial differential equations. He wrote an encyclopedic book on continued fractions ''Die Lehre von den Kettenbrüchen''. He introduced ''Perron's paradox'' to illustrate the danger of assuming that the solution of an optimization problem exists: :''Let N be the largest positive integer. If N > 1, then N2 > N, contradicting the definition of N. Hence N = 1''. Works * ''Ãœber die Drehung eines starren Körpers um seinen Schwerpunkt bei Wirkung äußerer Kräfte'', Diss. München 1902 * ''Grundlagen für eine Theorie der Jacobischen Kettenbruchalgorithmus'', Habilitationsschrift Leipzig 1906 * ''Die Lehre von den Kettenb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangulation (geometry)
In geometry, a triangulation is a subdivision of a planar object into triangles, and by extension the subdivision of a higher-dimension geometric object into simplices. Triangulations of a three-dimensional volume would involve subdividing it into tetrahedra packed together. In most instances, the triangles of a triangulation are required to meet edge-to-edge and vertex-to-vertex. Types Different types of triangulations may be defined, depending both on what geometric object is to be subdivided and on how the subdivision is determined. * A triangulation T of \mathbb^d is a subdivision of \mathbb^d into d-dimensional simplices such that any two simplices in T intersect in a common face (a simplex of any lower dimension) or not at all, and any bounded set in \mathbb^d intersects only finitely many simplices in T. That is, it is a locally finite simplicial complex that covers the entire space. * A point-set triangulation, i.e., a triangulation of a discrete set of points \mathcal\su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schönhardt Polyhedron
In geometry, the Schönhardt polyhedron is the simplest non-convex polyhedron that cannot be triangulated into tetrahedra without adding new vertices. It is named after German mathematician Erich Schönhardt, who described it in 1928. The same polyhedra have also been studied in connection with Cauchy's rigidity theorem as an example where polyhedra with two different shapes have faces of the same shapes. Construction One way of constructing the Schönhardt polyhedron starts with a triangular prism, with two parallel equilateral triangles as its faces. One of the triangles is rotated around the centerline of the prism, breaking the square faces of the prism into pairs of triangles. If each of these pairs is chosen to be non-convex, the Schönhardt polyhedron is the result. Properties The Schönhardt polyhedron has six vertices, twelve edges, and eight triangular faces. The six vertices of the Schönhardt polyhedron can be used to form fifteen unordered pairs of vertices. Twelv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
