|
Tempering (music)
In musical tuning, a temperament is a tuning system that slightly compromises the pure intervals of just intonation to meet other requirements. Most modern Western musical instruments are tuned in the equal temperament system. Tempering is the process of altering the size of an interval by making it narrower or wider than pure. "Any plan that describes the adjustments to the sizes of some or all of the twelve fifth intervals in the circle of fifths so that they accommodate pure octaves and produce certain sizes of major thirds is called a ''temperament''." Temperament is especially important for keyboard instruments, which typically allow a player to play only the pitches assigned to the various keys, and lack any way to alter pitch of a note in performance. Historically, the use of just intonation, Pythagorean tuning and meantone temperament meant that such instruments could sound "in tune" in one key, or some keys, but would then have more dissonance in other keys. In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Of Twelve Fifths
Comparison or comparing is the act of evaluating two or more things by determining the relevant, comparable characteristics of each thing, and then determining which characteristics of each are similar to the other, which are different, and to what degree. Where characteristics are different, the differences may then be evaluated to determine which thing is best suited for a particular purpose. The description of similarities and differences found between the two things is also called a comparison. Comparison can take many distinct forms, varying by field: To compare things, they must have characteristics that are similar enough in relevant ways to merit comparison. If two things are too different to compare in a useful way, an attempt to compare them is colloquially referred to in English as "comparing apples and oranges." Comparison is widely used in society, in science and in the arts. General usage Comparison is a natural activity, which even animals engage in when deci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the ratio of lemons to oranges is 6:8 (or 3:4) and the ratio of oranges to the total amount of fruit is 8:14 (or 4:7). The numbers in a ratio may be quantities of any kind, such as counts of people or objects, or such as measurements of lengths, weights, time, etc. In most contexts, both numbers are restricted to be positive. A ratio may be specified either by giving both constituting numbers, written as "''a'' to ''b''" or "''a'':''b''", or by giving just the value of their quotient Equal quotients correspond to equal ratios. Consequently, a ratio may be considered as an ordered pair of numbers, a fraction with the first number in the numerator and the second in the denominator, or as the value denoted by this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
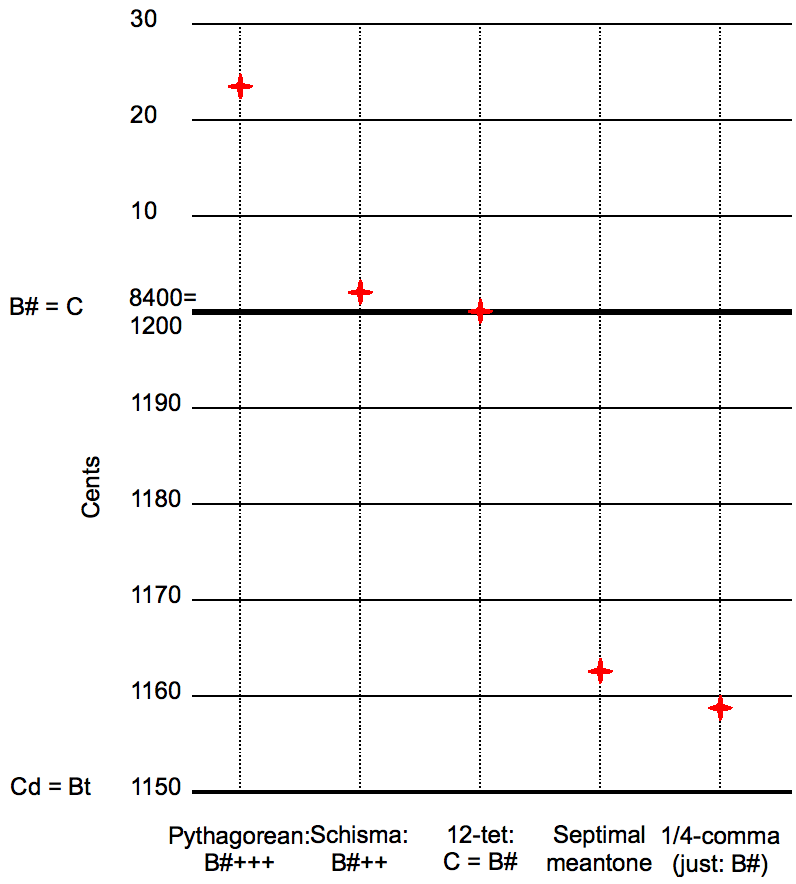
53 Equal Temperament
In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios). Each step represents a frequency ratio of 2, or 22.6415 cents (), an interval sometimes called the Holdrian comma. 53-TET is a tuning of equal temperament in which the tempered perfect fifth is 701.89 cents wide, as shown in Figure 1. The 53-TET tuning equates to the unison, or ''tempers out'', the intervals , known as the schisma, and , known as the kleisma. These are both 5 limit intervals, involving only the primes 2, 3 and 5 in their factorization, and the fact that 53 ET tempers out both characterizes it completely as a 5 limit temperament: it is the only regular temperament tempering out both of these intervals, or commas, a fact which seems to have first been recognized by Japanese music theorist Shohé Tanaka. Because it tempers these out, 53-TET can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wolf Interval
In music theory, the wolf fifth (sometimes also called Procrustean fifth, or imperfect fifth) Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction', p.165. Theodore Baker, trans. G. Schirmer. is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament. More broadly, it is also used to refer to similar intervals (of close, but variable magnitudes) produced by other tuning systems, including Pythagorean and most meantone temperaments. When the twelve notes within the octave of a chromatic scale are tuned using the quarter-comma mean-tone systems of temperament, one of the twelve intervals spanning seven semitones (classified as a diminished sixth) turns out to be much wider than the others (classified as perfect fifths). In mean-tone system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well Temperament And Equal Temperament
A well is an excavation or structure created in the ground by digging, driving, or drilling to access liquid resources, usually water. The oldest and most common kind of well is a water well, to access groundwater in underground aquifers. The well water is drawn up by a pump, or using containers, such as buckets or large water bags that are raised mechanically or by hand. Water can also be injected back into the aquifer through the well. Wells were first constructed at least eight thousand years ago and historically vary in construction from a simple scoop in the sediment of a dry watercourse to the qanats of Iran, and the stepwells and sakiehs of India. Placing a lining in the well shaft helps create stability, and linings of wood or wickerwork date back at least as far as the Iron Age. Wells have traditionally been sunk by hand digging, as is still the case in rural areas of the developing world. These wells are inexpensive and low-tech as they use mostly manual labour, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulation (music)
In music, modulation is the change from one tonality ( tonic, or tonal center) to another. This may or may not be accompanied by a change in key signature (a key change). Modulations articulate or create the structure or form of many pieces, as well as add interest. Treatment of a chord as the tonic for less than a phrase is considered tonicization. Requirements * Harmonic: quasi- tonic, modulating dominant, pivot chordForte (1979), p. 267. * Melodic: recognizable segment of the scale of the quasi-tonic or strategically placed leading-tone * Metric and rhythmic: quasi-tonic and modulating dominant on metrically accented beats, prominent pivot chord The quasi-tonic is the tonic of the new key established by the modulation was semi. The modulating dominant is the dominant of the quasi-tonic. The pivot chord is a predominant to the modulating dominant and a chord common to both the keys of the tonic and the quasi-tonic. For example, in a modulation to the dominant, ii/V– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quarter-comma Meantone
Quarter-comma meantone, or -comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81:80), with respect to its just intonation used in Pythagorean tuning (frequency ratio 3:2); the result is × () = ≈ 1.49535, or a fifth of 696.578 cents. (The 12th power of that value is 125, whereas 7 octaves is 128, and so falls 41.059 cents short.) This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds (with a frequency ratio equal to 5:4). It was described by Pietro Aron in his ''Toscanello de la Musica'' of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude. Construction In a meantone ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pietro Aron
Pietro Aron, also known as Pietro (or Piero) Aaron (c. 1480 – after 1545), was an Italian music theorist and composer. He was born in Florence and probably died in Bergamo (other sources state Florence or Venice). Biography Very little is known about Aron's early life but at least one source claims he may have been Jewish. He was educated in Italy. Aron was a self-taught musician. He claimed in his ''Toscanello in musica'' (1523) that he had been friends with Obrecht, Josquin, and Heinrich Isaac in Florence. If true, the time frame would have been most likely in 1487. Between 1515 and 1522, he was Church Cantor at the Cathedral of Imola. In 1516 he became a priest there. In February 1523 Aron went to Venice and became cantor of Rimini Cathedral, where he worked for Sebastiano Michiel, who was Grand Prior of the Knights of St. John of Jerusalem. In 1525, he was "maestro di casa" in a Venetian house. In 1536, after the death of Michiel, he joined a monastery in Bergamo where h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) (around 21.51 cents). Two notes that differ by this interval would sound different from each other even to untrained ears, , ''BBC''. but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tertian
In music theory, ''tertian'' ( la, tertianus, "of or concerning thirds") describes any piece, chord, counterpoint etc. constructed from the intervals of ( major and minor) thirds. An interval such as that between the notes A and C encompasses 3 semitone intervals (A-B-B-C) and is termed a minor third while one such as that between C and E encompasses 4 semitones (C-D-D-E-E) and is called a major third. Tertian harmony (also called tertiary harmony ) principally uses chords based on thirds; the term is typically used to contrast with quartal and quintal harmony which uses chords based on fourths or fifths. A common triad chord can be regarded as consisting of a "stack" of two consecutive thirds. This allows for four permutations, each producing a chord with distinct quality: A musical scale may also be analyzed as a succession of thirds. The meantone temperament, a system of tuning that emphasizes pure thirds, may be called "tertian". Chords built from sixths may als ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartal Harmony
In music, quartal harmony is the building of harmonic structures built from the intervals of the perfect fourth, the augmented fourth and the diminished fourth. For instance, a three-note quartal chord on C can be built by stacking perfect fourths, C–F–B. : Quintal harmony is harmonic structure preferring the perfect fifth, the augmented fifth and the diminished fifth. For instance, a three-note quintal chord on C can be built by stacking perfect fifths, C–G–D. : Properties Use of the terms ''quartal'' and ''quintal'' arises from a contrast, compositional or perceptual, with traditional tertian harmonic constructions. Listeners familiar with music of the European common practice period perceive tonal music as that which uses major and minor chords and scales, wherein both the major third and minor third constitute the basic ''structural elements'' of the harmony. Regarding chords built from perfect fourths alone, composer Vincent Persichetti writes tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |