|
Schönflies Notation
The Schoenflies (or Schönflies) notation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation. Although Schoenflies notation without superscripts is a pure point group notation, optionally, superscripts can be added to further specify individual space groups. However, for space groups, the connection to the underlying symmetry elements is much more clear in Hermann–Mauguin notation, so the latter not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Germans
, native_name_lang = de , region1 = , pop1 = 72,650,269 , region2 = , pop2 = 534,000 , region3 = , pop3 = 157,000 3,322,405 , region4 = , pop4 = 21,000 3,000,000 , region5 = , pop5 = 125,000 982,226 , region6 = , pop6 = 900,000 , region7 = , pop7 = 142,000 840,000 , region8 = , pop8 = 9,000 500,000 , region9 = , pop9 = 357,000 , region10 = , pop10 = 310,000 , region11 = , pop11 = 36,000 250,000 , region12 = , pop12 = 25,000 200,000 , region13 = , pop13 = 233,000 , region14 = , pop14 = 211,000 , region15 = , pop15 = 203,000 , region16 = , pop16 = 201,000 , region17 = , pop17 = 101,000 148,00 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and nature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
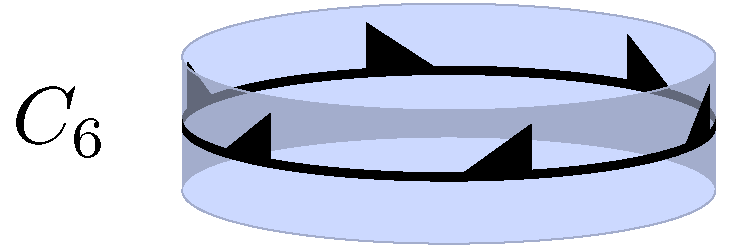
List Of Spherical Symmetry Groups
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry. This article lists the groups by Schoenflies notation, Coxeter notation, orbifold notation, and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion. Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.Sands, 1993 Involutional symmetry There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-fold rotational symmetry (C2), and cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Groups In Three Dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetries. All isometries of a bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with E+(3), which consists of all ''direct isometries'', i.e., isometries preserving orientation. For a bounded object, the proper sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Space Groups
There are 230 space groups in three dimensions, given by a number index, and a full name in Hermann–Mauguin notation, and a short name (international short symbol). The long names are given with spaces for readability. The groups each have a point group of the unit cell. Symbols In Hermann–Mauguin notation, space groups are named by a symbol combining the point group identifier with the uppercase letters describing the lattice type. Translations within the lattice in the form of screw axes and glide planes are also noted, giving a complete crystallographic space group. These are the Bravais lattices in three dimensions: *P primitive *I body centered (from the German ''Innenzentriert'') *F face centered (from the German ''Flächenzentriert'') *A centered on A faces only *B centered on B faces only *C centered on C faces only *R rhombohedral A reflection plane m within the point groups can be replaced by a glide plane, labeled as a, b, or c depending on which axis the glide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by Function composition, composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrix, orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose invertible matrix, inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact group, compact. The orthogonal group in dimension has two connected component (topology), connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curie Group
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetries. All isometries of a bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with E+(3), which consists of all ''direct isometries'', i.e., isometries preserving orientation. For a bounded object, the proper symme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallographic Point Group
In crystallography, a crystallographic point group is a set of symmetry operations, corresponding to one of the point groups in three dimensions, such that each operation (perhaps followed by a translation) would leave the structure of a crystal unchanged i.e. the same kinds of atoms would be placed in similar positions as before the transformation. For example, in many crystals in the cubic crystal system, a rotation of the unit cell by 90 degrees around an axis that is perpendicular to one of the faces of the cube is a symmetry operation that moves each atom to the location of another atom of the same kind, leaving the overall structure of the crystal unaffected. In the classification of crystals, each point group defines a so-called (geometric) crystal class. There are infinitely many three-dimensional point groups. However, the crystallographic restriction on the general point groups results in there being only 32 crystallographic point groups. These 32 point groups are one-and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Improper Rotation
In geometry, an improper rotation,. also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason it is also called a rotoinversion or rotary inversion. The two definitions are equivalent because rotation by an angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystallographic Restriction Theorem
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. However, quasicrystals can occur with other diffraction pattern symmetries, such as 5-fold; these were not discovered until 1982 by Dan Shechtman.Shechtman et al (1982) Crystals are modeled as discrete lattices, generated by a list of independent finite translations . Because discreteness requires that the spacings between lattice points have a lower bound, the group of rotational symmetries of the lattice at any point must be a finite group (alternatively, the point is the only system allowing for infinite rotational symmetry). The strength of the theorem is that ''not all'' finite groups are compatible with a discrete lattice; in any dimension, we will have only a finite number of compatible groups. Dimensions 2 and 3 The special cases of 2D (wallpaper groups) and 3D (space groups) are most ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)

.png)

