|
Point Groups In Three Dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group (mathematics), group of all isometry, isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrix, orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetry, symmetries. All isometries of a Bounded set, bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the Origin (mathematics), origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with Euclidean group#Direct and indirect is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chirality (mathematics)
In geometry, a figure is chiral (and said to have chirality) if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by Rotation (mathematics), rotations and Translation (geometry), translations alone. An object that is not chiral is said to be ''achiral''. A chiral object and its mirror image are said to be enantiomorphs. The word ''chirality'' is derived from the Greek (cheir), the hand, the most familiar chiral object; the word ''enantiomorph'' stems from the Greek (enantios) 'opposite' + (morphe) 'form'. Examples Some chiral three-dimensional objects, such as the helix, can be assigned a right or left handedness, according to the right-hand rule. Many other familiar objects exhibit the same chiral symmetry of the human body, such as gloves and shoes. Right shoes differ from left shoes only by being mirror images of each other. In contrast thin gloves may not be considered chiral if you can wear them wiktionary:inside ou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumflex
The circumflex () is a diacritic in the Latin and Greek scripts that is also used in the written forms of many languages and in various romanization and transcription schemes. It received its English name from "bent around"a translation of the (). The circumflex in the Latin script is chevron-shaped (), while the Greek circumflex may be displayed either like a tilde () or like an inverted breve (). For the most commonly encountered uses of the accent in the Latin alphabet, precomposed characters are available. In English, the circumflex, like other diacritics, is sometimes retained on loanwords that used it in the original language (for example '' entrepôt, crème brûlée''). In mathematics and statistics, the circumflex diacritic is sometimes used to denote a function and is called a '' hat operator''. A free-standing version of the circumflex symbol, , is encoded in ASCII and Unicode and has become known as '' caret'' and has acquired special uses, particularly i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Improper Rotation
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a Rotation (geometry), rotation about an axis and a reflection (mathematics), reflection in a plane perpendicular to that axis. Reflection and Point reflection, inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of Symmetry (geometry), geometric symmetry, molecular symmetry and Crystallographic point group, crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Set Of A Group
In abstract algebra, a generating set of a group is a subset of the group set such that every element of the group (mathematics), group can be expressed as a combination (under the group operation) of finitely many elements of the subset and their Inverse element, inverses. In other words, if S is a subset of a group G, then \langle S\rangle, the ''subgroup generated by S'', is the smallest subgroup of G containing every element of S, which is equal to the intersection over all subgroups containing the elements of S; equivalently, \langle S\rangle is the subgroup of all elements of G that can be expressed as the finite product of elements in S and their inverses. (Note that inverses are only needed if the group is infinite; in a finite group, the inverse of an element can be expressed as a power of that element.) If G=\langle S\rangle, then we say that S ''generates'' G, and the elements in S are called ''generators'' or ''group generators''. If S is the empty set, then \langle S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schoenflies Notation
The Schoenflies (or Schönflies) notation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation. Although Schoenflies notation without superscripts is a pure point group notation, optionally, superscripts can be added to further specify individual space groups. However, for space groups, the connection to the underlying symmetry elements is much more clear in Hermann–Mauguin notation, so the latter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called '' 3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a '' solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Operation
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a turn rotation of a regular triangle about its center (geometry), center, a reflection (mathematics), reflection of a square across its diagonal, a translation (geometry), translation of the Euclidean plane, or a point reflection of a sphere through its center are all symmetry operations. Each symmetry operation is performed with respect to some symmetry element (a point, line or plane). In the context of molecular symmetry, a symmetry operation is a permutation of atoms such that the molecule or crystal is transformed into a state indistinguishable from the starting state. Two basic facts follow from this definition, which emphasizes its usefulness. # Physical properties must be Invariant (physics), invariant with respect to symmetry operations. # Symmetry operations can be collected together in groups which are isomo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Character Tables For Chemically Important 3D Point Groups
This lists the character tables for the more common point groups in three dimensions, molecular point groups used in the study of molecular symmetry. These tables are based on the group theory, group-theoretical treatment of the symmetry operations present in common molecules, and are useful in molecular spectroscopy and quantum chemistry. Information regarding the use of the tables, as well as more extensive lists of them, can be found in the references. Notation For each non-linear group, the tables give the most standard notation of the finite group isomorphic to the point group, followed by the Order (group theory), order of the group (number of invariant symmetry operations). The finite group notation used is: Zn: cyclic group of order ''n'', Dn: dihedral group isomorphic to the symmetry group of an ''n''–sided regular polygon, Sn: symmetric group on ''n'' letters, and An: alternating group on ''n'' letters. The character tables then follow for all groups. The rows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covalent Bond
A covalent bond is a chemical bond that involves the sharing of electrons to form electron pairs between atoms. These electron pairs are known as shared pairs or bonding pairs. The stable balance of attractive and repulsive forces between atoms, when they share electrons, is known as covalent bonding. For many molecules, the sharing of electrons allows each atom to attain the equivalent of a full valence shell, corresponding to a stable electronic configuration. In organic chemistry, covalent bonding is much more common than ionic bonding. Covalent bonding also includes many kinds of interactions, including σ-bonding, π-bonding, metal-to-metal bonding, agostic interactions, bent bonds, three-center two-electron bonds and three-center four-electron bonds. The term "covalence" was introduced by Irving Langmuir in 1919, with Nevil Sidgwick using "co-valent link" in the 1920s. Merriam-Webster dates the specific phrase ''covalent bond'' to 1939, recognizing its first known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
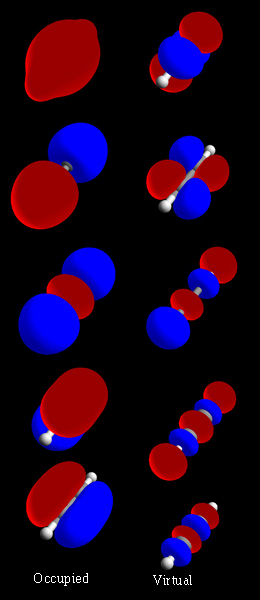
Molecular Orbital
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms ''atomic orbital'' and ''molecular orbital'' were introduced by Robert S. Mulliken in 1932 to mean ''one-electron orbital wave functions''. At an elementary level, they are used to describe the ''region'' of space in which a function has a significant amplitude. In an isolated atom, the orbital electrons' location is determined by functions called atomic orbitals. When multiple atoms combine chemically into a molecule by forming a valence chemical bond, the electrons' locations are determined by the molecule as a whole, so the atomic orbitals combine to form molecular orbitals. The electrons from the constituent atoms occupy the molecular orbitals. Mathematically, molecular orbitals are an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemistry, and biochemistry, the distinction from ions is dropped and ''molecule'' is often used when referring to polyatomic ions. A molecule may be homonuclear, that is, it consists of atoms of one chemical element, e.g. two atoms in the oxygen molecule (O2); or it may be heteronuclear, a chemical compound composed of more than one element, e.g. water (molecule), water (two hydrogen atoms and one oxygen atom; H2O). In the kinetic theory of gases, the term ''molecule'' is often used for any gaseous particle regardless of its composition. This relaxes the requirement that a molecule contains two or more atoms, since the noble gases are individual atoms. Atoms and complexes connected by non-covalent interactions, such as hydrogen bonds or ionic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |