|
Saffman–Delbrück Model
The Saffman–Delbrück model describes a Lipid bilayer, lipid membrane as a thin layer of Viscous liquid, viscous fluid, surrounded by a less viscous bulk liquid. This picture was originally proposed to determine the diffusion coefficient of membrane proteins, but has also been used to describe the dynamics of fluid domains within lipid membranes. The Saffman–Delbrück formula is often applied to determine the size of an object embedded in a membrane from its observed Brownian motion, diffusion coefficient, and is characterized by the weak logarithmic dependence of diffusion constant on object radius. Origin In a three-dimensional highly viscous liquid, a spherical object of radius ''a'' has diffusion coefficient : D_ = \frac by the well-known Stokes–Einstein relation. By contrast, the diffusion coefficient of a circular object embedded in a two-dimensional fluid diverges; this is Stokes' paradox. In a real lipid membrane, the diffusion coefficient may be limited by: # t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lipid Bilayer
The lipid bilayer (or phospholipid bilayer) is a thin polar membrane made of two layers of lipid molecules. These membranes are flat sheets that form a continuous barrier around all cells. The cell membranes of almost all organisms and many viruses are made of a lipid bilayer, as are the nuclear membrane surrounding the cell nucleus, and membranes of the membrane-bound organelles in the cell. The lipid bilayer is the barrier that keeps ions, proteins and other molecules where they are needed and prevents them from diffusing into areas where they should not be. Lipid bilayers are ideally suited to this role, even though they are only a few nanometers in width, because they are impermeable to most water-soluble (hydrophilic) molecules. Bilayers are particularly impermeable to ions, which allows cells to regulate salt concentrations and pH by transporting ions across their membranes using proteins called ion pumps. Biological bilayers are usually composed of amphiphilic phosphol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscous Liquid
In condensed matter physics and physical chemistry, the terms viscous liquid, supercooled liquid, and glassforming liquid are often used interchangeably to designate liquids that are at the same time highly viscous (see Viscosity of amorphous materials), can be or are supercooled, and able to form a glass. Working points in glass processing The mechanical properties of glass-forming liquids depend primarily on the viscosity. Therefore, the following working points are defined in terms of viscosity. The temperature is indicated for industrial soda lime glass: Fragile-strong classification In a widespread classification, due to chemist Austen Angell, a glass-forming liquid is called strong if its viscosity approximately obeys an Arrhenius law (log η is linear in 1/''T'' ). In the opposite case of clearly non-Arrhenius behaviour the liquid is called fragile. This classification has no direct relation with the common usage of the word "fragility" to mean brittlene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas). This pattern of motion typically consists of random fluctuations in a particle's position inside a fluid sub-domain, followed by a relocation to another sub-domain. Each relocation is followed by more fluctuations within the new closed volume. This pattern describes a fluid at thermal equilibrium, defined by a given temperature. Within such a fluid, there exists no preferential direction of flow (as in transport phenomena). More specifically, the fluid's overall linear and angular momenta remain null over time. The kinetic energies of the molecular Brownian motions, together with those of molecular rotations and vibrations, sum up to the caloric component of a fluid's internal energy (the equipartition theorem). This motion is named after the botanist Robert Brown, who first described the phenomenon in 1827, while looking throu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes–Einstein Relation
In physics (specifically, the kinetic theory of gases), the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation is D = \mu \, k_\text T, where * is the diffusion coefficient; * is the "mobility", or the ratio of the particle's terminal drift velocity to an applied force, ; * is the Boltzmann constant; * is the absolute temperature. This equation is an early example of a fluctuation-dissipation relation. Two frequently used important special forms of the relation are: * Einstein–Smoluchowski equation, for diffusion of charged particles: D = \frac * Stokes–Einstein equation, for diffusion of spherical particles through a liquid with low Reynolds number: D = \frac Here * is the electrical charge of a particle; * is the electrical mobility of the charged particle; * is the dyna ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes' Paradox
In the science of fluid flow, Stokes' paradox is the phenomenon that there can be no creeping flow of a fluid around a disk in two dimensions; or, equivalently, the fact there is no non-trivial steady-state solution for the Stokes equations around an infinitely long cylinder. This is opposed to the 3-dimensional case, where Stokes' method provides a solution to the problem of flow around a sphere. Derivation The velocity vector \mathbf of the fluid may be written in terms of the stream function \psi as : \mathbf = \left(\frac, - \frac\right). The stream function in a Stokes flow problem, \psi satisfies the biharmonic equation. By regarding the (x,y)-plane as the complex plane, the problem may be dealt with using methods of complex analysis. In this approach, \psi is either the real or imaginary part of : \bar f(z) + g(z). Here z = x + iy, where i is the imaginary unit, \bar = x - iy, and f(z), g(z) are holomorphic functions outside of the disk. We will take the real par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow ( eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip Saffman
Philip Geoffrey Saffman FRS (19 March 1931 – 17 August 2008) was a mathematician and the Theodore von Kármán Professor of Applied Mathematics and Aeronautics at the California Institute of Technology.. Education and early life Saffman was born to a Jewish family in Leeds, England, and educated at Roundhay Grammar School and Trinity College, Cambridge which he entered aged 15. He received his Bachelor of Arts degree in 1953, studied for Part III of the Cambridge Mathematical Tripos in 1954 and was awarded his PhD in 1956 for research supervised by George Batchelor. Career and research Saffman started his academic career as a lecturer at the University of Cambridge, then joined King's College London as a Reader. Saffman joined the Caltech faculty in 1964 and was named the Theodore von Kármán Professor in 1995. According to Dan Meiron, Saffman "really was one of the leading figures in fluid mechanics," and he influenced almost every subfield of that discipline. He is known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Delbrück
Max Ludwig Henning Delbrück (; September 4, 1906 – March 9, 1981) was a German–American biophysicist who participated in launching the molecular biology research program in the late 1930s. He stimulated physical science, physical scientists' interest into biology, especially as to basic research to physically explain genes, mysterious at the time. Formed in 1945 and led by Delbrück along with Salvador Luria and Alfred Hershey, the Phage Group made substantial headway unraveling important aspects of genetics. The three shared the 1969 Nobel Prize in Physiology or Medicine "for their discoveries concerning the replication mechanism and the genetic structure of viruses"."The Nobel Prize in Physiology or Medicine 1969" Nobel Media AB 2013, ''Nobelprize.org'', Web access November 6, 2013. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
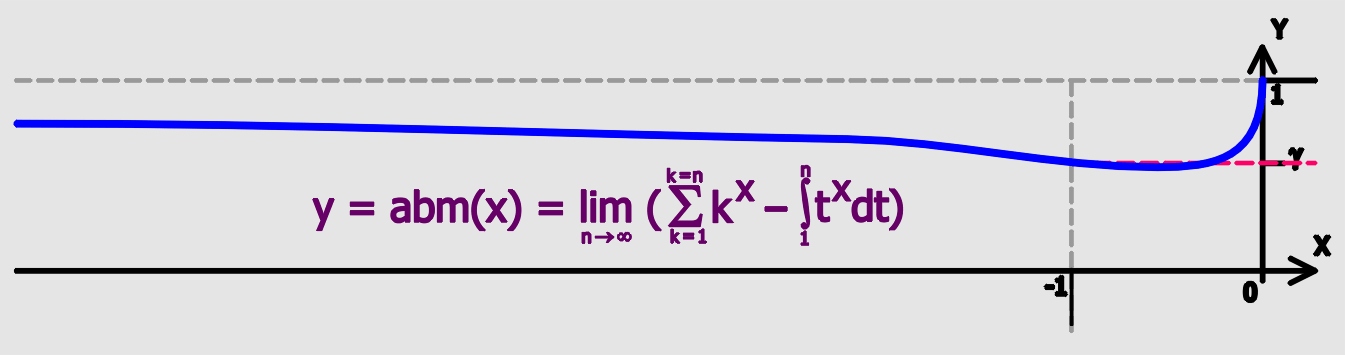
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |