|
Strongly Correlated Materials
Strongly correlated materials are a wide class of compounds that include insulators and electronic materials, and show unusual (often technologically useful) electronic and magnetic properties, such as metal-insulator transitions, heavy fermion behavior, half-metallicity, and spin-charge separation. The essential feature that defines these materials is that the behavior of their electrons or spinons cannot be described effectively in terms of non-interacting entities. Theoretical models of the electronic (fermionic) structure of strongly correlated materials must include electronic (fermionic) correlation to be accurate. As of recently, the label quantum materials is also used to refer to strongly correlated materials, among others. Transition metal oxides Many transition metal oxides belong to this class which may be subdivided according to their behavior, ''e.g.'' high-Tc, spintronic materials, multiferroics, Mott insulators, spin Peierls materials, heavy fermion material ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
High-temperature Superconductivity
High-temperature superconductors (abbreviated high-c or HTS) are defined as materials that behave as superconductors at temperatures above , the boiling point of liquid nitrogen. The adjective "high temperature" is only in respect to previously known superconductors, which function at even colder temperatures close to absolute zero. In absolute terms, these "high temperatures" are still far below ambient, and therefore require cooling. The first high-temperature superconductor was discovered in 1986, by IBM researchers Bednorz and Müller, who were awarded the Nobel Prize in Physics in 1987 "for their important break-through in the discovery of superconductivity in ceramic materials". Most high-c materials are type-II superconductors. The major advantage of high-temperature superconductors is that they can be cooled by using liquid nitrogen, as opposed to the previously known superconductors which require expensive and hard-to-handle coolants, primarily liquid helium. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
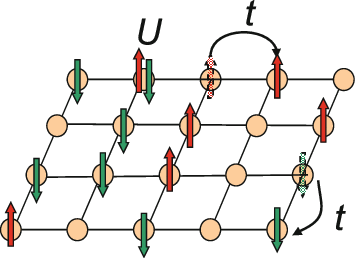
Hubbard Model
The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed to be in the lowest Bloch band, and long-range interactions between the particles can be ignored. If interactions between particles at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GW Approximation
The ''GW'' approximation (GWA) is an approximation made in order to calculate the self-energy of a many-body system of electrons. The approximation is that the expansion of the self-energy ''Σ'' in terms of the single particle Green's function ''G'' and the screened Coulomb interaction ''W'' (in units of \hbar=1) : \Sigma = iGW - GWGWG + \cdots can be truncated after the first term: : \Sigma \approx iG W In other words, the self-energy is expanded in a formal Taylor series in powers of the screened interaction ''W'' and the lowest order term is kept in the expansion in GWA. Theory The above formulae are schematic in nature and show the overall idea of the approximation. More precisely, if we label an electron coordinate with its position, spin, and time and bundle all three into a composite index (the numbers 1, 2, etc.), we have : \Sigma(1,2) = iG(1,2)W(1^+,2) - \int d3 \int d4 \, G(1,3)G(3,4)G(4,2)W(1,4)W(3,2) + ... where the "+" superscript means the time index is shif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band Gap
In solid-state physics, a band gap, also called an energy gap, is an energy range in a solid where no electronic states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference (in electron volts) between the top of the valence band and the bottom of the conduction band in insulators and semiconductors. It is the energy required to promote a valence electron bound to an atom to become a conduction electron, which is free to move within the crystal lattice and serve as a charge carrier to conduct electric current. It is closely related to the HOMO/LUMO gap in chemistry. If the valence band is completely full and the conduction band is completely empty, then electrons cannot move within the solid because there are no available states. If the electrons are not free to move within the crystal lattice, then there is no generated current due to no net charge carrier mobility. However, if some electrons transfer from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Repulsion
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is conventionally called ''electrostatic force'' or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb, hence the name. Coulomb's law was essential to the development of the theory of electromagnetism, maybe even its starting point, as it made it possible to discuss the quantity of electric charge in a meaningful way. The law states that the magnitude of the electrostatic force of attraction or repulsion between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them. Coulomb studied the repulsive force between bodies having electrical charges of the same sign: Coulomb also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
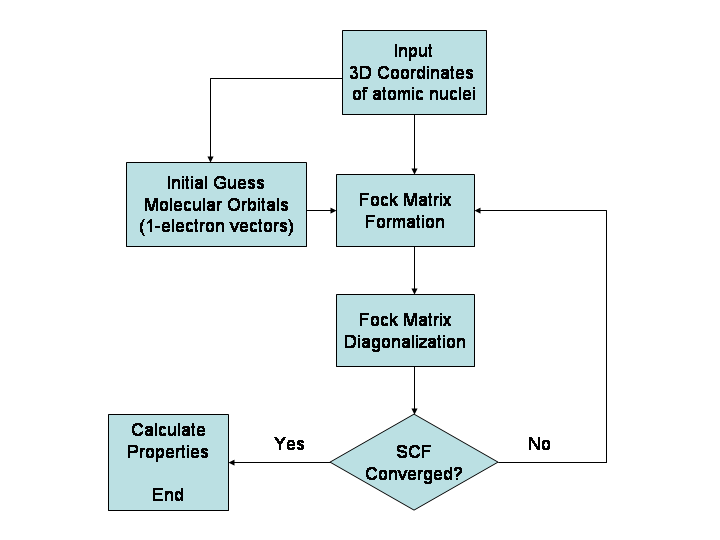
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density-functional Theory
Density-functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990s, when the approximations used in the theory were greatly refined to better model the exchange and correlation interactions. Comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local-density Approximation
Local-density approximations (LDA) are a class of approximations to the exchange–correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space (and not, for example, derivatives of the density or the Kohn–Sham orbitals). Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems (molecules and solids). In general, for a spin-unpolarized system, a local-density approximation for the exchange-correlation energy is written as :E_^rho= \int \rho(\mathbf)\epsilon_(\rho(\mathbf))\ \mathrm\mathbf\ , where ''ρ'' is the electronic density and ''ε''xc is the exchange-correlation energy per particle of a homogeneous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligence, epidemic models, queueing theory, computer-network p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Sea
A composite fermion is the topological bound state of an electron and an even number of quantized vortices, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect, but subsequently took on a life of their own, exhibiting many other consequences and phenomena. Vortices are an example of topological defect, and also occur in other situations. Quantized vortices are found in type II superconductors, called Abrikosov vortices. Classical vortices are relevant to the Berezenskii–Kosterlitz–Thouless transition in two-dimensional XY model. Description When electrons are confined to two dimensions, cooled to very low temperatures, and subjected to a strong magnetic field, their kinetic energy is quenched due to Landau level quantization. Their behavior under such conditions is governed by the Coulomb repulsion alone, and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |