|
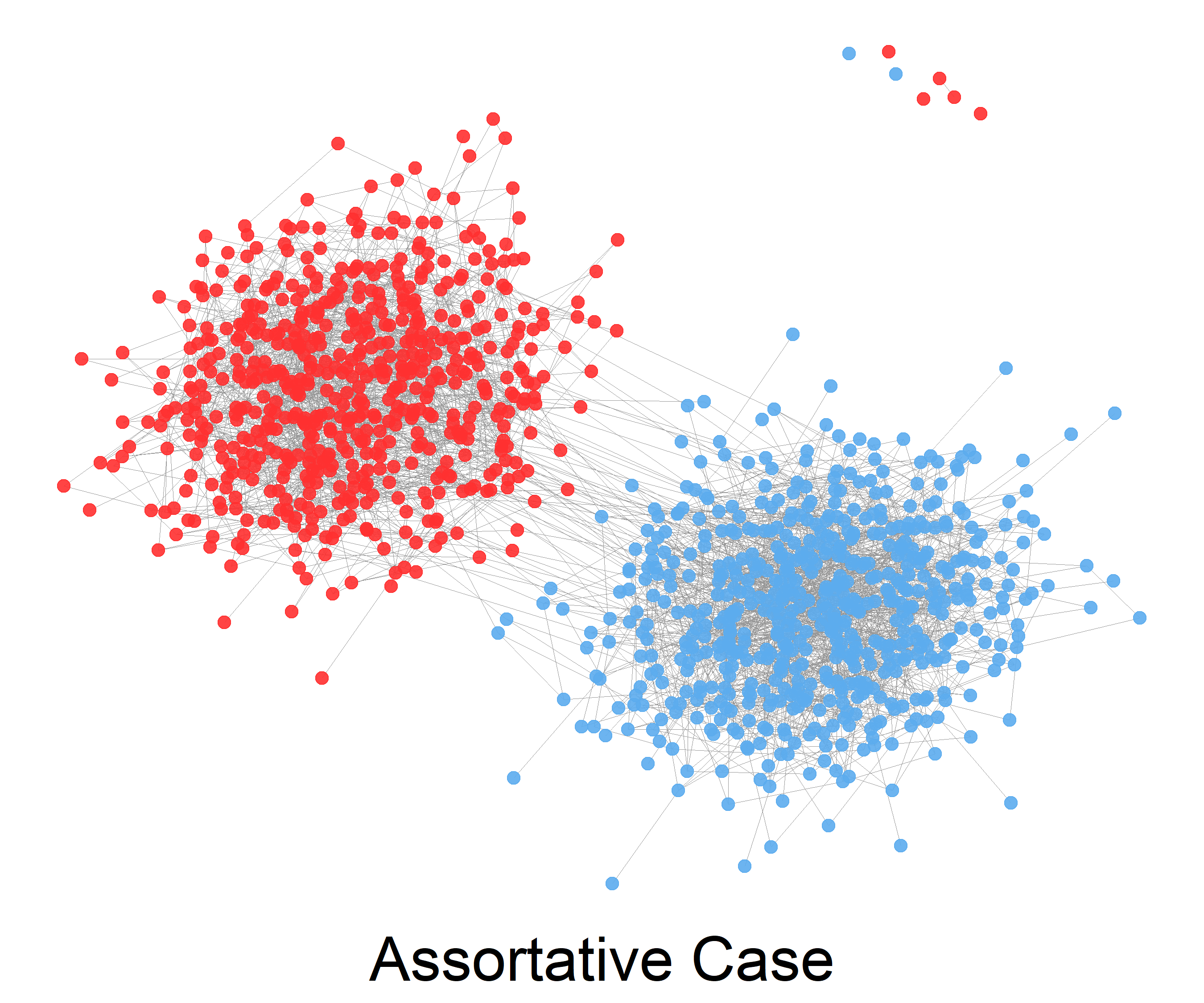
Stochastic Block Model
The stochastic block model is a generative model for random graphs. This model tends to produce graphs containing ''communities'', subsets of nodes characterized by being connected with one another with particular edge densities. For example, edges may be more common within communities than between communities. Its mathematical formulation has been firstly introduced in 1983 in the field of social network by Holland et al. The stochastic block model is important in statistics, machine learning, and network science, where it serves as a useful benchmark for the task of recovering community structure in graph data. Definition The stochastic block model takes the following parameters: * The number n of vertices; * a partition of the vertex set \ into disjoint subsets C_1,\ldots,C_r, called ''communities''; * a symmetric r \times r matrix P of edge probabilities. The edge set is then sampled at random as follows: any two vertices u \in C_i and v \in C_j are connected by an edge w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blockmodel
Blockmodel (sometimes also block model) in blockmodeling (part of network science) is defined as a multitude of structures, which are obtained with: * identification of all vertices (e.g., units, nodes) within a cluster and at the same time representing each cluster as a vertex, from which vertices for another graph can be constructed; * combination of all the links (ties), represented in a block as a single link between positions, while at the same time constructing one tie for each block. In a case, when there are no ties in a block, there will be no ties between the two positions, that define the block. In principle, blockmodeling, as a process, is composed from three steps. In the first step, the number of units is determined. This is followed (in the second step) by selection or determination of permitted blocks, that will occur and perhaps also the locations in the matrix. The last, third step, using computer program, the partitioning of units is done, according to the pre- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Networks
A social network is a social structure made up of a set of social actors (such as individuals or organizations), sets of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities as well as a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine network dynamics. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of triads and "web of group affiliations". Jacob Moreno is credited with developing the first sociograms in the 1930s to study interpersonal relationships. These approaches were mathematically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blockmodeling
Blockmodeling is a set or a coherent framework, that is used for analyzing social structure and also for setting procedure(s) for partitioning (clustering) social network's units ( nodes, vertices, actors), based on specific patterns, which form a distinctive structure through interconnectivity. Patrick Doreian, An Intuitive Introduction to Blockmodeling with Examples, ''BMS: Bulletin of Sociological Methodology'' / ''Bulletin de Méthodologie Sociologique'', January, 1999, No. 61 (January, 1999), pp. 5–34. It is primarily used in statistics, machine learning and network science. As an empirical procedure, blockmodeling assumes that all the units in a specific network can be grouped together to such extent to which they are equivalent. Regarding equivalency, it can be structural, regular or generalized. Anuška Ferligoj: Blockmodeling, http://mrvar.fdv.uni-lj.si/sola/info4/nusa/doc/blockmodeling-2.pdf Using blockmodeling, a network can be analyzed using newly created block ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretations, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topic Model
In statistics and natural language processing, a topic model is a type of statistical model for discovering the abstract "topics" that occur in a collection of documents. Topic modeling is a frequently used text-mining tool for discovery of hidden semantic structures in a text body. Intuitively, given that a document is about a particular topic, one would expect particular words to appear in the document more or less frequently: "dog" and "bone" will appear more often in documents about dogs, "cat" and "meow" will appear in documents about cats, and "the" and "is" will appear approximately equally in both. A document typically concerns multiple topics in different proportions; thus, in a document that is 10% about cats and 90% about dogs, there would probably be about 9 times more dog words than cat words. The "topics" produced by topic modeling techniques are clusters of similar words. A topic model captures this intuition in a mathematical framework, which allows examining a set o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Distribution
In probability theory and statistics, a categorical distribution (also called a generalized Bernoulli distribution, multinoulli distribution) is a discrete probability distribution that describes the possible results of a random variable that can take on one of ''K'' possible categories, with the probability of each category separately specified. There is no innate underlying ordering of these outcomes, but numerical labels are often attached for convenience in describing the distribution, (e.g. 1 to ''K''). The ''K''-dimensional categorical distribution is the most general distribution over a ''K''-way event; any other discrete distribution over a size-''K'' sample space is a special case. The parameters specifying the probabilities of each possible outcome are constrained only by the fact that each must be in the range 0 to 1, and all must sum to 1. The categorical distribution is the generalization of the Bernoulli distribution for a categorical random variable, i.e. for a di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Belief Propagation
A belief is an attitude that something is the case, or that some proposition is true. In epistemology, philosophers use the term "belief" to refer to attitudes about the world which can be either true or false. To believe something is to take it to be true; for instance, to believe that snow is white is comparable to accepting the truth of the proposition "snow is white". However, holding a belief does not require active introspection. For example, few carefully consider whether or not the sun will rise tomorrow, simply assuming that it will. Moreover, beliefs need not be ''occurrent'' (e.g. a person actively thinking "snow is white"), but can instead be ''dispositional'' (e.g. a person who if asked about the color of snow would assert "snow is white"). There are various different ways that contemporary philosophers have tried to describe beliefs, including as representations of ways that the world could be (Jerry Fodor), as dispositions to act as if certain things are true (Ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semidefinite Programming
Semidefinite programming (SDP) is a subfield of convex optimization concerned with the optimization of a linear objective function (a user-specified function that the user wants to minimize or maximize) over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron. Semidefinite programming is a relatively new field of optimization which is of growing interest for several reasons. Many practical problems in operations research and combinatorial optimization can be modeled or approximated as semidefinite programming problems. In automatic control theory, SDPs are used in the context of linear matrix inequalities. SDPs are in fact a special case of cone programming and can be efficiently solved by interior point methods. All linear programs and (convex) quadratic programs can be expressed as SDPs, and via hierarchies of SDPs the solutions of polynomial optimization problems can be approximated. Semidefinite programming has been ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretations, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, a problem is NP-complete when: # it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # the problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, "nondeterministic" refers to nondeterministic Turing machines, a way of mathematically formalizing the idea of a brute-force search algorithm. Polynomial time refers to an amount of time that is considered "quick" for a det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |