|
Stefan Problem
In mathematics and its applications, particularly to phase transitions in matter, a Stefan problem is a particular kind of boundary value problem for a system of partial differential equations (PDE), in which the boundary between the phases can move with time. The classical Stefan problem aims to describe the evolution of the boundary between two phases of a material undergoing a phase change, for example the melting of a solid, such as ice to water. This is accomplished by solving heat equations in both regions, subject to given boundary and initial conditions. At the interface between the phases (in the classical problem) the temperature is set to the phase change temperature. To close the mathematical system a further equation, the Stefan condition, is required. This is an energy balance which defines the position of the moving interface. Note that this evolving boundary is an unknown (hyper-)surface; hence, Stefan problems are examples of free boundary problems. Analogous p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-posed Problem
The mathematical term well-posed problem stems from a definition given by 20th-century French mathematician Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that: # a solution exists, # the solution is unique, # the solution's behaviour changes continuously with the initial conditions. Examples of archetypal well-posed problems include the Dirichlet problem for Laplace's equation, and the heat equation with specified initial conditions. These might be regarded as 'natural' problems in that there are physical processes modelled by these problems. Problems that are not well-posed in the sense of Hadamard are termed ill-posed. Inverse problems are often ill-posed. For example, the inverse heat equation, deducing a previous distribution of temperature from final data, is not well-posed in that the solution is highly sensitive to changes in the final data. Continuum models must often be discretized in order to obtain a numerica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cahn–Hilliard Equation
The Cahn–Hilliard equation (after John W. Cahn and John E. Hilliard) is an equation of mathematical physics which describes the process of phase separation, by which the two components of a binary fluid spontaneously separate and form domains pure in each component. If c is the concentration of the fluid, with c=\pm1 indicating domains, then the equation is written as :\frac = D\nabla^2\left(c^3-c-\gamma\nabla^2 c\right), where D is a diffusion coefficient with units of \text^2/\text and \sqrt gives the length of the transition regions between the domains. Here \partial/ is the partial time derivative and \nabla^2 is the Laplacian in n dimensions. Additionally, the quantity \mu = c^3-c-\gamma\nabla^2 c is identified as a chemical potential. Related to it is the Allen–Cahn equation, as well as the stochastic Cahn–Hilliard Equation and the stochastic Allen–Cahn equation. Features and applications Of interest to mathematicians is the existence of a unique solution of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Equation
In applied mathematics, a transcendental equation is an equation over the real number, real (or complex number, complex) numbers that is not algebraic equation, algebraic, that is, if at least one of its sides describes a transcendental function. Examples include: :\begin x &= e^ \\ x &= \cos x \\ 2^x &= x^2 \end A transcendental equation need not be an equation between elementary functions, although most published examples are. In some cases, a transcendental equation can be solved by transforming it into an equivalent algebraic equation. Some such transformations are sketched #Transformation into an algebraic equation, below; computer algebra systems may provide more elaborated transformations. In general, however, only approximate solutions can be found. Transformation into an algebraic equation Ad hoc methods exist for some classes of transcendental equations in one variable to transform them into algebraic equations which then might be solved. Exponential equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan Number
The Stefan number (St or Ste) is defined as the ratio of sensible heat to latent heat. It is given by the formula \mathrm = \frac, where * ''cp'' is the specific heat, ** cp is the specific heat of solid phase in the freezing process while cp is the specific heat of liquid phase in the melting process. * ∆''T'' is the temperature difference between phases, * ''L'' is the latent heat of melting. It is a dimensionless parameter that is useful in analyzing a Stefan problem. The parameter was developed from Josef Stefan's calculations of the rate of phase change of water into ice on the polar ice caps and coined by G.S.H. Lock in 1969. The problems origination is fully described by Vuik and further commentary on its place in Josef Stefan Josef Stefan ( sl, Jožef Štefan; 24 March 1835 – 7 January 1893) was an ethnic Carinthian Slovene physicist, mathematician, and poet of the Austrian Empire. Life and work Stefan was born in an outskirt village of St. Peter (Slovene: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sensible Heat
Sensible heat is heat exchanged by a body or thermodynamic system in which the exchange of heat changes the temperature of the body or system, and some macroscopic variables of the body or system, but leaves unchanged certain other macroscopic variables of the body or system, such as volume or pressure. Usage The term is used in contrast to a latent heat, which is the amount of heat exchanged that is hidden, meaning it occurs without change of temperature. For example, during a phase change such as the melting of ice, the temperature of the system containing the ice and the liquid is constant until all ice has melted. The terms latent and sensible are correlative. The sensible heat of a thermodynamic process may be calculated as the product of the body's mass (''m'') with its specific heat capacity (''c'') and the change in temperature (\Delta T): : Q_ = m c \Delta T \, . ''Sensible heat'' and ''latent heat'' are not special forms of energy. Rather, they describe exchanges of hea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nondimensionalization
Nondimensionalization is the partial or full removal of physical dimensions from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis. In some physical systems, the term scaling is used interchangeably with ''nondimensionalization'', in order to suggest that certain quantities are better measured relative to some appropriate unit. These units refer to quantities intrinsic to the system, rather than units such as SI units. Nondimensionalization is not the same as converting extensive quantities in an equation to intensive quantities, since the latter procedure results in variables that still carry units. Nondimensionalization can also recover characteristic properties of a system. For example, if a system has an intrinsic resonance frequency, length, or time constant, nondimensionalization can recover these val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Xavier Ros-Oton
Xavier Ros Oton (Barcelona, 1988) is a Spanish mathematician who works on partial differential equations (PDEs). He is an ICREA Research Professor and a Full Professor at the University of Barcelona. Research His research is mainly focused on topics related to the regularity of solutions to nonlinear elliptic and parabolic PDE. Some of his main contributions have been in the context of free boundary problems, integro-differential equations, and the Calculus of Variations. Career He earned his Bachelor's and Master's degree at the Universitat Politècnica de Catalunya in 2010 and 2011, and completed his PhD in 2014 under the supervision of Xavier Cabré. He then moved to the University of Texas at Austin, where he was an R. H. Bing Instructor, and worked with Alessio Figalli and Luis Caffarelli. After that, he was an assistant professor at the University of Zurich. Since 2020, Ros-Oton is an ICREA Research Professor at the University of Barcelona. He is a member of the editorial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alessio Figalli
Alessio Figalli (; born 2 April 1984) is an Italian mathematician working primarily on calculus of variations and partial differential equations. He was awarded the Prix and in 2012, the EMS Prize in 2012, the Stampacchia Medal in 2015, the Feltrinelli Prize in 2017, and the Fields Medal in 2018. He was an invited speaker at the International Congress of Mathematicians 2014. In 2016 he was awarded a European Research Council (ERC) grant, and in 2018 he received the Doctorate Honoris Causa from the Université Côte d'Azur. In 2019, he received the Doctorate Honoris Causa from the Polytechnic University of Catalonia. Biography Figalli received his master's degree from the University of Pisa in 2006 (as a student of the Scuola Normale Superiore di Pisa), and earned his doctorate in 2007 under the supervision of Luigi Ambrosio at the Scuola Normale Superiore di Pisa and Cédric Villani at the École Normale Supérieure de Lyon. In 2007, he was appointed Chargé de recherche at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luis Caffarelli
Luis Angel Caffarelli (born December 8, 1948) is an Argentine mathematician and luminary in the field of partial differential equations and their applications. Career Caffarelli was born and grew up in Buenos Aires. He obtained his Masters of Science (1968) and Ph.D. (1972) at the University of Buenos Aires. His Ph.D. advisor was Calixto Calderón. He currently holds the Sid Richardson Chair at the University of Texas at Austin. He also has been a professor at the University of Minnesota, the University of Chicago, and the Courant Institute of Mathematical Sciences at New York University. From 1986 to 1996 he was a professor at the Institute for Advanced Study in Princeton. Important results Caffarelli received great recognition with his breakthrough paper "The regularity of free boundaries in higher dimensions" published in 1977 in ''Acta Mathematica''. Since then, he has been considered one of the world's leading experts in free boundary problems and nonlinear partial differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Heat
Latent heat (also known as latent energy or heat of transformation) is energy released or absorbed, by a body or a thermodynamic system, during a constant-temperature process — usually a first-order phase transition. Latent heat can be understood as energy in hidden form which is supplied or extracted to change the state of a substance without changing its temperature. Examples are latent heat of fusion and latent heat of vaporization involved in phase changes, i.e. a substance condensing or vaporizing at a specified temperature and pressure. The term was introduced around 1762 by Scottish chemist Joseph Black. It is derived from the Latin ''latere'' (''to lie hidden''). Black used the term in the context of calorimetry where a heat transfer caused a volume change in a body while its temperature was constant. In contrast to latent heat, sensible heat is energy transferred as heat, with a resultant temperature change in a body. Usage The terms ″sensible heat″ and ″laten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
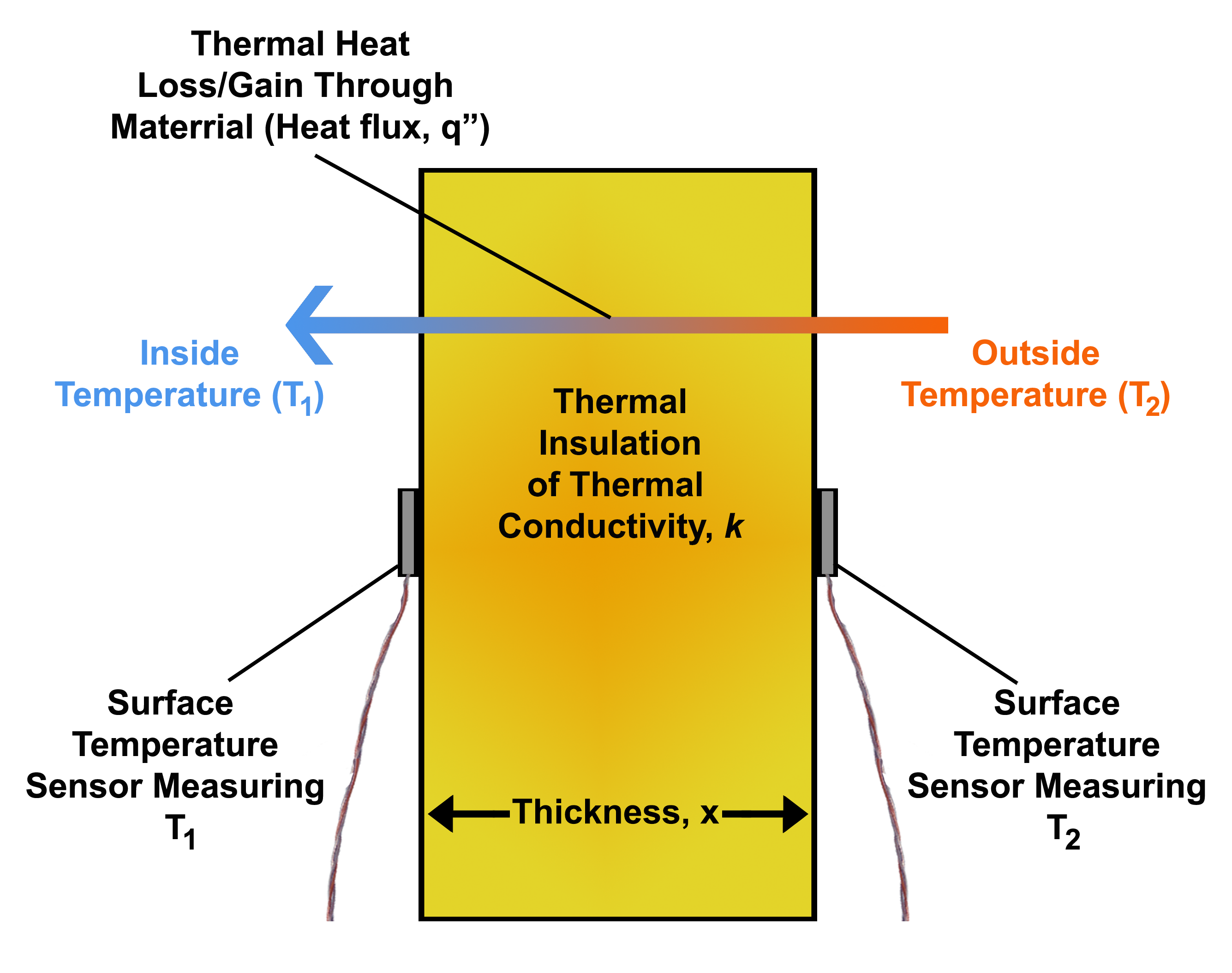
Heat Flux
Heat flux or thermal flux, sometimes also referred to as ''heat flux density'', heat-flow density or ''heat flow rate intensity'' is a flow of energy per unit area per unit time. In SI its units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''mass'' or ''momentum'' flux. Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi_\text = -k \frac where k is the thermal conductivity. The negative sign shows that heat flux moves from higher temperature regions to lower temperature regions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
